Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Tích vô hướng của hai vectơ (HAY NHẤT 2024) gồm đầy đủ các phần: Lý thuyết, phương pháp giải, bài tập minh họa có lời giải chi tiết giúp học sinh làm tốt bài tập Toán 10 từ đó học tốt môn Toán. Mời các bạn đón xem:
Nội dung bài viết
Phương pháp giải Tích vô hướng của hai vectơ (HAY NHẤT 2024)
A. Lí thuyết
- Định nghĩa góc giữa hai vectơ: Cho hai vectơ và đều khác vectơ . Từ điểm O bất kì vẽ , , khi đó góc () là góc giữa hai vectơ và . Kí hiệu: .
- Định nghĩa tích vô hướng: Cho hai vectơ và (), khi đó tích vô hướng của và kí hiệu là và xác định bởi công thức: .
- Chú ý:
+) Khi ít nhất một trong hai vectơ và bằng vectơ ta quy ước: .
+) Với hai vectơ và (), ta có: .
+) Tích vô hướng được kí hiệu là và ta có: .
- Các tính chất của tích vô hướng:
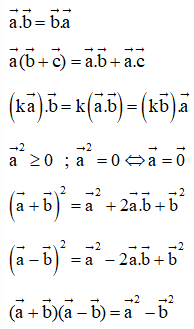
- Biểu thức tọa độ của tích vô hướng: Trong mặt phẳng , cho hai vectơ và . Khi đó: . Và với hai vectơ và đều khác thì .
- Ứng dụng của tích vô hướng:
+) Độ dài của vectơ được tính theo công thức:
+) Góc giữa hai vectơ và ( ):
+) Khoảng cách giữa hai điểm và được tính theo công thức:
B. Các dạng bài
Dạng 1: Tính tích vô hướng của hai vectơ, góc giữa hai vectơ.
Phương pháp giải:
- Tính tích vô hướng: Phân tích vectơ và đưa hai vectơ về chung gốc để tìm góc giữa hai vectơ hoặc đưa hai vectơ về các vectơ vuông góc. Sau đó, áp dụng công thức định nghĩa, tính chất và hằng đẳng thức để tính tích vô hướng của hai vectơ. Đối với hai vectơ biết tọa độ thì tính theo công thức
- Tính góc giữa hai vectơ: Phân tích vectơ và đưa hai vectơ về chung gốc để tìm góc giữa hai vectơ hoặc dùng công thức:
Ví dụ minh họa:
Bài 1: Cho tam giác ABC đều cạnh 2a có đường cao AH. Tính các tích vô hướng và
Lời giải:
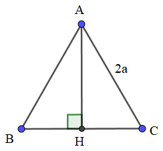
Vì tam giác ABC đều nên ta có:
Ta có:
Vì AH là đường cao nên ta có:
Bài 2: Cho hình chữ nhật ABCD. Biết AB = 2a, AD = a và . Tính các góc giữa các cặp vectơ sau: và .
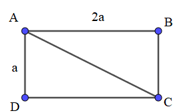
Lời giải:
Vì ABCD là hình chữ nhật nên ta có: BC // AD và BC = AD
( do ABCD là hình chữ nhật )
Xét tam giác ABC vuông tại B.
Áp dụng định lý Py-ta-go ta có:
Áp dụng công thức tính góc giữa hai vec tơ và ta có:
Dạng 2: Tính độ dài đoạn thẳng, độ dài vectơ.
Phương pháp giải:
Phân tích vectơ để biến phép tính độ dài đoạn thẳng thành phép tính tích vô hướng, áp dụng công thức . Nếu đề bài có liên quan đến tọa độ thì áp dụng công thức: .
Ví dụ minh họa:
Bài 1: Cho tam giác ABC, biết AB = a, AC = 2a, . Tính độ dài cạnh BC.
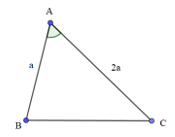
Lời giải:
Áp dụng quy tắc ba điểm ta có:
Ta có: ;
Bài 2: Cho hai điểm A (4;5) và B (2;3). Tính độ dài đoạn thẳng AB.
Lời giải:
Độ dài đoạn thẳng AB chính là khoảng cách giữa hai điểm A và B.
Áp dụng công thức tính khoảng cách giữa hai điểm A (4;5) và B (2;3) ta có:
Dạng 3: Chứng minh vuông góc.
Phương pháp giải:
Dùng tích chất của tích vô hướng để chứng minh vuông góc:
Hoặc dùng công thức về tọa độ:
Ví dụ minh họa:
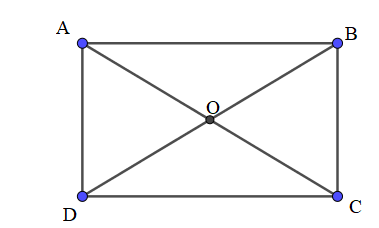
Bài 1: Cho hình vuông ABCD tâm O. Chứng minh hai đường chéo AC và BD vuông góc bằng cách áp dụng tích vô hướng.
Lời giải
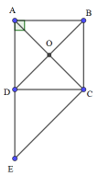
Từ C vẽ CE sao cho CE = BD và CE // BD.
Ta có:
Xét hình vuông ABCD có
Xét hình bình hành BCED có: (hai góc đối)
Ta có AD cắt CE tại E. Có vì ABCD là hình vuông
Xét tam giác CDE vuông tại D có:
Từ đó ta có :
( do )
Khi đó ta có:
Vậy hai đường chéo AC và BD vuông góc với nhau.
Bài 2: Cho đoạn thẳng AB có trung điểm O, điểm M tùy ý khác O, A, B và không thuộc AB, biết 4OM2 = AB2. Hãy chứng minh rằng MA 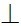 MB.
MB.
Lời giải:
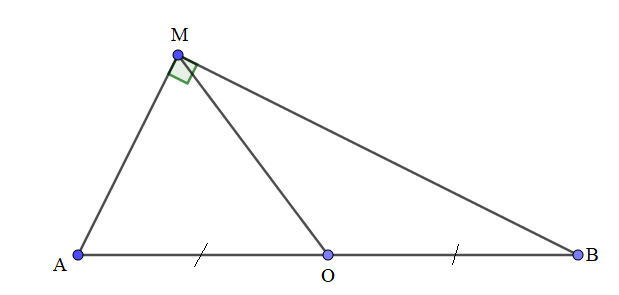
4OM2 = AB2.
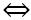 (2OM)2 = AB2.
(2OM)2 = AB2.
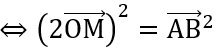
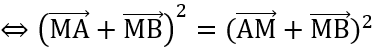
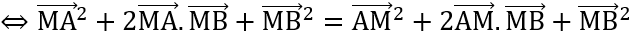
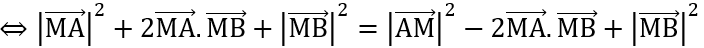
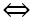 MA2 + 2
MA2 + 2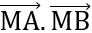 + MB2 = AM2 - 2
+ MB2 = AM2 - 2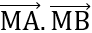 + MB2
+ MB2
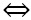 2
2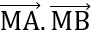 + 2
+ 2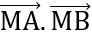 = 0
= 0
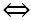 4
4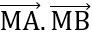 = 0
= 0
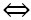
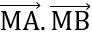 = 0
= 0
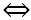
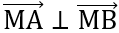
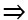 MA
MA 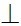 MB ( điều cần phải chứng minh )
MB ( điều cần phải chứng minh )
Dạng 4: Chứng minh các đẳng thức về tích vô hướng hay độ dài.
Phương pháp giải:
Áp dụng định nghĩa và tính chất của tích vô hướng, các quy tắc phân tích, biến đổi vectơ, các công thức về độ dài vectơ để biến đổi sao cho hai vế bằng nhau hoặc từ giả thiết suy ra một biểu thức luôn đúng đã được công nhận. Để chứng minh 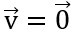 ta có thể chứng minh tích vô hướng của
ta có thể chứng minh tích vô hướng của 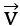 với hai vectơ khác không cùng phương bằng 0.
với hai vectơ khác không cùng phương bằng 0.
Ví dụ minh họa:
Bài 1: Cho tam giác ABC bất kì có I là trung điểm của AB. Chứng minh đẳng thức: CA2 + CB2 = 2CI2 + 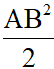
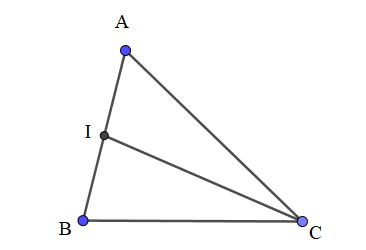
Lời giải:
Ta có: VP = 2CI2 + 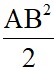
 2VP = 4CI2 + AB2
2VP = 4CI2 + AB2
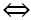 2VP = 4
2VP = 4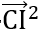 +
+ 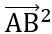
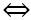 2VP = (2
2VP = (2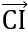 )2 + (
)2 + (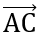 +
+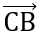 )2
)2
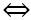 2VP = (
2VP = (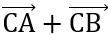 )2 + (
)2 + (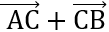 )2
)2
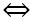 2VP =
2VP = 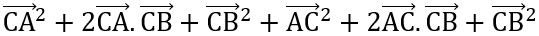
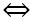 2VP = CA2 + 2
2VP = CA2 + 2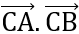 + CB2 + AC2 - 2
+ CB2 + AC2 - 2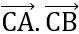 + CB2
+ CB2
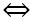 2VP = 2CA2 + 2CB2
2VP = 2CA2 + 2CB2
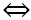 VP = CA2 + CB2 = VT
VP = CA2 + CB2 = VT
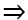 CA2 + CB2 = 2CI2 +
CA2 + CB2 = 2CI2 + 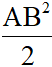 ( điều cần phải chứng minh )
( điều cần phải chứng minh )
Bài 2: Cho 4 điểm A, B, C, D bất kì. Chứng minh: 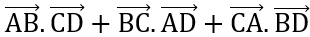 = 0
= 0
Lời giải:
Ta có:

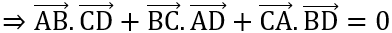 (điều cần phải chứng minh)
(điều cần phải chứng minh)
Dạng 5: Các bài toán liên quan đến biểu thức tọa độ.
Phương pháp giải:
Áp dụng các công thức, tính chất của tích vô hướng liên quan đến tọa độ để giải quyết các yêu cầu của đề bài.
Ví dụ minh họa:
Bài 1: Cho vectơ 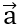 = (-1;2). Tìm tọa độ vectơ
= (-1;2). Tìm tọa độ vectơ 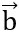 cùng phương với
cùng phương với 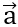 và thỏa mãn
và thỏa mãn 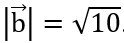
Lời giải:
Gọi vectơ 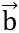 = (x;y) .
= (x;y) .
Vì vectơ 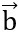 cùng phương với
cùng phương với 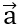 nên ta có :
nên ta có : 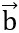 = k
= k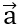 (k
(k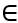 R)
R)
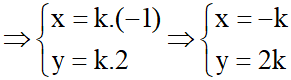
Áp dụng công thức tính độ dài của vectơ 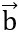 ta có:
ta có:
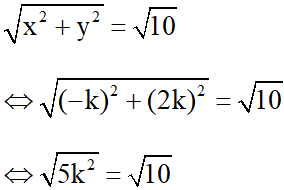
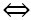 5k2 = 10
5k2 = 10
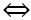 k2 = 2
k2 = 2
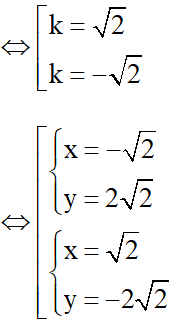
 hoặc
hoặc 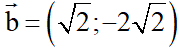
Bài 2: Cho hai vectơ 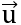 = (1;3) và
= (1;3) và 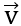 = (x;1). Tìm x sao cho
= (x;1). Tìm x sao cho 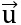
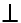
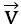
Lời giải:
Ta có: 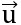 .
.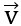 = 1.x + 3.1 = 3 + x
= 1.x + 3.1 = 3 + x
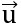

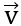
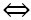
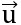 .
.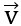 = 0
= 0 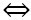 3 + x = 0
3 + x = 0
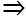 x = -3
x = -3
Vậy khi x = -3 thì 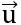
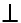
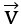 .
.
Dạng 6: Tìm tọa độ các điểm đặc biệt trong tam giác.
Phương pháp giải:
Áp dụng định nghĩa, tính chất, các công thức của tích vô hướng liên quan đến tọa độ, các quy tắc trung điểm, quy tắc trọng tâm để tính tọa độ điểm đặc biệt. Ta có:
- Trung điểm I (x;y) của đoạn thẳng AB với A(xA;yA) và B(xA;yA): x = 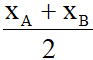 ; y=
; y= 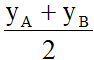 - Trọng tâm G (x;y) của tam giác ABC với A(xA;yA), B(xA;yA) và C(xC;yC):
- Trọng tâm G (x;y) của tam giác ABC với A(xA;yA), B(xA;yA) và C(xC;yC):
x = 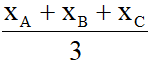 ;y =
;y = 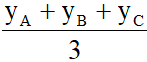
- Trực tâm H (x;y) của tam giác ABC, ta có: 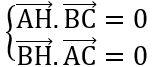
Giải hệ trên ta tìm được x, y.
- Chân đường cao K (x;y) vẽ từ đỉnh A, ta có: 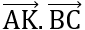 = 0 (1) và
= 0 (1) và 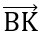 cùng phương với
cùng phương với 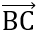 (2) ( do B, K, C thẳng hàng) . Từ hai điều kiện (1), (2) lập phương trình để tìm ra x, y.
(2) ( do B, K, C thẳng hàng) . Từ hai điều kiện (1), (2) lập phương trình để tìm ra x, y.
- Tâm đường tròn ngoại tiếp I (x;y) của tam giác ABC. Nếu tam giác ABC vuông tại A thì I là trung điểm của BC. Nếu tam giác ABC đều thì I là trọng tâm. Nếu tam giác ABC là tam giác thường thì có theo hệ 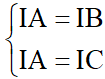 hoặc gọi M, N là trung điểm của BC và AC, có hệ
hoặc gọi M, N là trung điểm của BC và AC, có hệ 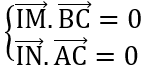 . Từ hệ phương trình tìm được x, y.- Điểm D (x;y) là chân đường phân giác trong của góc A, ta có:
. Từ hệ phương trình tìm được x, y.- Điểm D (x;y) là chân đường phân giác trong của góc A, ta có: 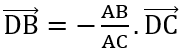
- Điểm E (x;y) là chân đường phân giác ngoài của góc A, ta có: 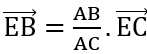
- Tâm đường tròn nội tiếp K (x;y) của tam giác ABC có BC = a, AC = b, AB = c và A(xA;yA), B(xA;yA), C(xC;yC). Tìm điểm D là chân đường phân giác trong của góc A của tam giác ABC. Lúc đó điểm K là chân đường phân giác trong của góc B của tam giác ABD. Hoặc dùng công thức:
xK = 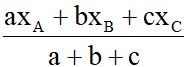 ; yK =
; yK = 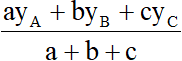 . ( đối với bài toán trắc nghiệm )
. ( đối với bài toán trắc nghiệm )
Ví dụ minh họa:
Bài 1: Cho tam giác ABC, biết A (1;1), B (1;7), C (9;1). Tìm điểm K là tâm đường tròn nội tiếp, điểm O là tâm đường tròn ngoại tiếp tam giác ABC.
Lời giải:
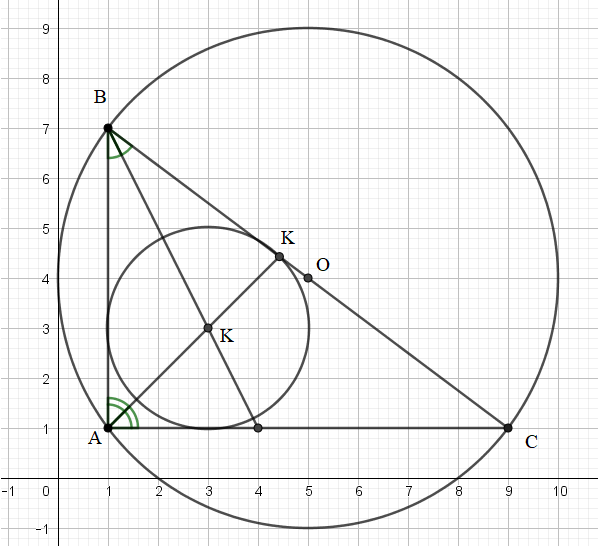
Gọi K (x;y) là tâm đường tròn nội tiếp và D(xD;yD) là chân đường phân giác trong của góc A trong tam giác ABC.
Xét tam giác ABC, ta có:
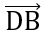 = (1-xD;7-yD)
= (1-xD;7-yD)
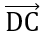 = (9-xD;1-yD)
= (9-xD;1-yD)
AB = 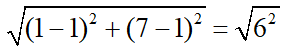 = 6
= 6
AC = 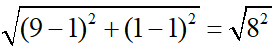 = 8
= 8
Áp dụng công thức về chân đường phân giác trong ta có:
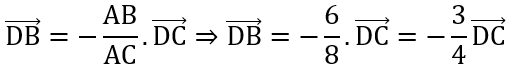
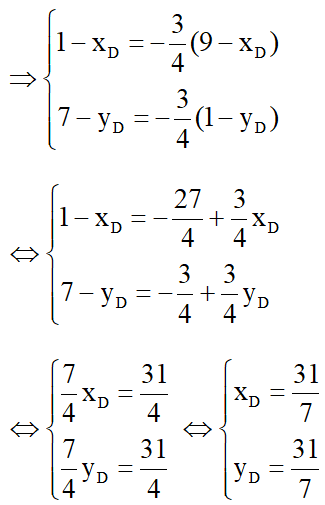
Xét tam giác ABD ta có:
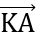 = (1-x;1-y)
= (1-x;1-y)
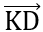 =
= 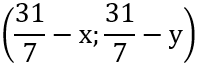
BA = 6
BD = 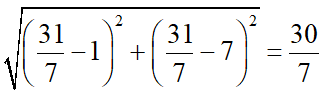
Áp dụng công thức về chân đường phân giác trong ta có:
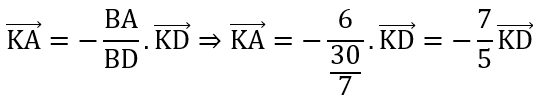
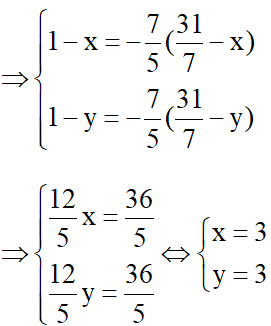
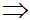 K = (3;3)
K = (3;3)
Ta có:
AB = 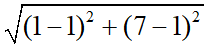 = 6
= 6
AC = 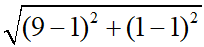 = 8
= 8
BC = 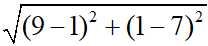 = 10
= 10
62 + 82 = 100 = 102
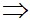 BC2 = AB2 + AC2
BC2 = AB2 + AC2
 Tam giác ABC vuông tại A.
Tam giác ABC vuông tại A.
 Tâm đường tròn ngoại tiếp tức điểm O(xO;yO) là trung điểm của BC.
Tâm đường tròn ngoại tiếp tức điểm O(xO;yO) là trung điểm của BC.
Áp dụng công thức tính tọa độ trung điểm ta có:
xO = 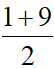 =5
=5
yO = 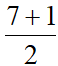 = 4
= 4
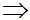 O (5;4)
O (5;4)
Bài 2: Cho tam giác ABC biết A (4;3), B (-1;-1), C (2;-4). Tìm tọa độ trung điểm M của AB, trực tâm H, trọng tâm I của tam giác ABC.
Lời giải:
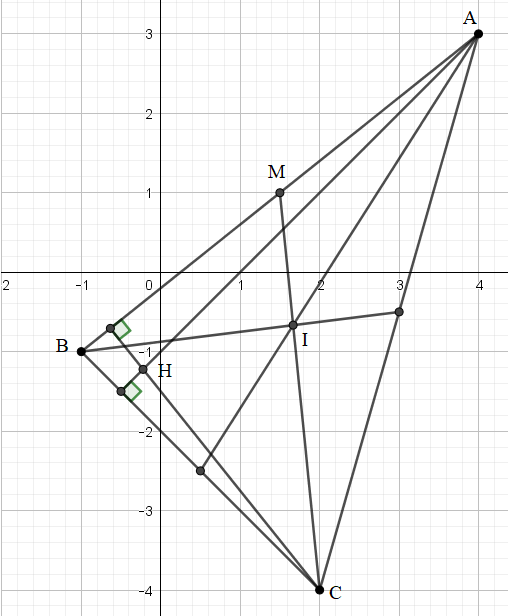
Gọi điểm M(xM;yM) là trung điểm của AB.
Áp dụng công thức tọa độ trung điểm ta có:
xM = 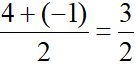
yM = 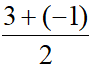 = 1
= 1
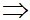 M
M 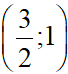
Gọi trực tâm H = (x;y) là giao điểm của 3 đường cao thuộc tam giác ABC.
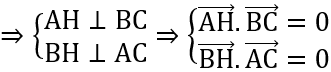
Ta có:
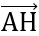 = (x-4; y-3)
= (x-4; y-3)
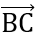 = (3;-3)
= (3;-3)
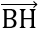 = (x+1;y+1)
= (x+1;y+1)
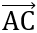 = (-2;-7)
= (-2;-7)
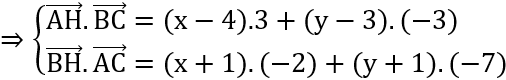
Ta có:
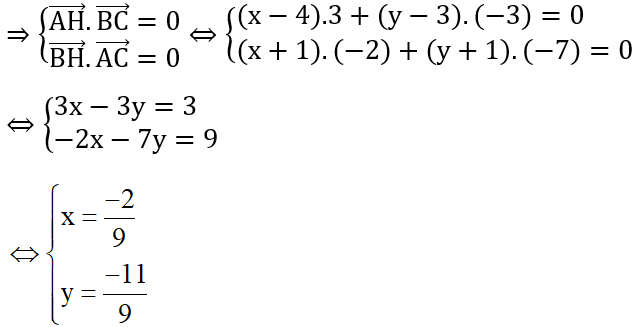
 H =
H = 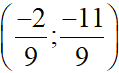
Gọi điểm I(xI;yI) là trọng tâm tam giác ABC.
Áp dụng công thức tính trọng tâm tam giác ta có:
xI = 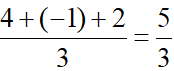
yI = 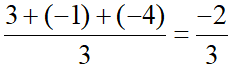
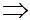 H =
H = 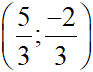
Dạng 7: Các bài toán liên quan đến dạng tam giác, tứ giác.
Phương pháp giải:
- Dạng chứng minh:
+) Chứng minh tam giác ABC cân tại A: Ta cần tính độ dài AB, AC, sau đó chứng minh AB = AC.
+) Chứng minh tam giác ABC vuông tại A: Tính độ dài AB, AC, BC và chứng minh AB2 + AC2 = BC2. Hoặc tính tích vô hướng 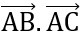 và chứng minh nó bằng 0.+) Chứng minh tam giác ABC vuông cân tại A: Ta cần chứng minh:
và chứng minh nó bằng 0.+) Chứng minh tam giác ABC vuông cân tại A: Ta cần chứng minh:
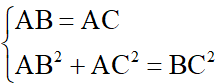 hoặc
hoặc 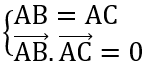
+) Chứng minh tứ giác ABCD là hình bình hành: Tính độ dài AB, DC và chứng minh 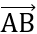 =
= 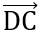
+) Chứng minh tứ giác ABCD là hình thoi: Tính AB, BC, CD, DA và chứng minh AB = BC = CD = DA .
+) Chứng minh tứ giác ABCD là hình chữ nhật: Ta cần chứng minh ABCD là hình bình hành có 1 góc vuông hoặc chứng minh ABCD là hình bình hành có hai đường chéo bằng nhau.
+) Chứng minh tứ giác ABCD là hình vuông: Ta cần chứng minh ABCD là hình thoi có 1 góc vuông hoặc chứng minh ABCD là hình bình hành có 1 góc vuông và hai cạnh liên tiếp bằng nhau.
+) Chứng minh tứ giác ABCD là hình thang. Chứng minh 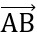 ,
, 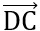 cùng phương. Nếu chứng minh hình thang vuông thì chứng minh thêm 1 góc vuông. Nếu chứng minh hình thang cân thì chứng minh thêm 2 đường chéo bằng nhau.
cùng phương. Nếu chứng minh hình thang vuông thì chứng minh thêm 1 góc vuông. Nếu chứng minh hình thang cân thì chứng minh thêm 2 đường chéo bằng nhau.
+) Chứng minh tứ giác ABCD là tứ giác nội tiếp: Chứng minh các góc vuông cần thiết bằng cách áp dụng tích vô hướng và suy ra tứ giác nội tiếp.
- Dạng tìm tọa độ điểm:
+) Tìm tọa độ điểm M thuộc trục tung (hoặc trục hoành) để tam giác MAB vuông tại M với A, B cho trước. Nếu M 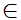 Ox
Ox  M(x;0) và nếu M
M(x;0) và nếu M 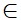 Oy
Oy  M(0;y). Tính tọa độ
M(0;y). Tính tọa độ 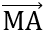 ,
,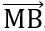 , tìm x hoặc y sao cho
, tìm x hoặc y sao cho 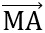 .
.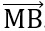 = 0.
= 0.
+) Tìm tọa độ điểm N thuộc trục tung (hoặc hoành) để tam giác MAB cân tại M và A, B là hai điểm cho trước. Nếu N 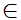 Ox
Ox  N(x;0) và nếu N
N(x;0) và nếu N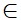 Oy
Oy  N(0;y). Tính độ dài NA, NB và tìm x hoặc y sao cho NA = NB. ( loại tọa độ N ứng với trung điểm của AB ).+) Tìm tọa độ điểm P thuộc trục tung (hoặc hoành) để P, A, B thẳng hàng và A, B là hai điểm cho trước. Nếu P
N(0;y). Tính độ dài NA, NB và tìm x hoặc y sao cho NA = NB. ( loại tọa độ N ứng với trung điểm của AB ).+) Tìm tọa độ điểm P thuộc trục tung (hoặc hoành) để P, A, B thẳng hàng và A, B là hai điểm cho trước. Nếu P 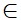 Ox
Ox  P(x;0)và nếu P
P(x;0)và nếu P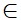 Oy
Oy  N(0;y). Tìm x hoặc y sao cho
N(0;y). Tìm x hoặc y sao cho 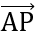 ,
, 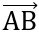 cùng phương.
cùng phương.
Ví dụ minh họa:
Bài 1: Trong mặt phẳng Oxy, chứng minh tứ giác ABCD là hình chữ nhật . Biết tọa độ các điểm A (-1;2), B (1;4), C (5;0), D (3;-2).
Lời giải:
Ta có:
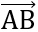 = (2;2) ;
= (2;2) ; 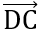 = (2;2)
= (2;2)
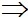
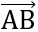 =
= 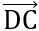
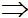 ABCD là hình bình hành
ABCD là hình bình hành
Ta có: 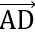 = (4;-4)
= (4;-4)
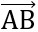 .
. 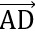 = 2.4 + 2.(-4) = 0
= 2.4 + 2.(-4) = 0
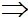
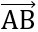
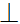
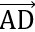
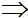
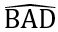 =
= 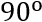
Xét hình bình hành ABCD có: 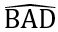 =
= 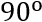
Tứ giác ABCD là hình chữ nhật ( điều cần phải chứng minh )
Bài 2: Cho hai điểm A (-3;3) và B (4;4). Tìm điểm M thuộc trục tung để tam giác MAB vuông tại M.
Lời giải:
M thuộc trung tung nên ta gọi M = (0;y).
Ta có:
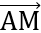 = (3;y-3);
= (3;y-3); 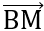 = (-4;y-4)
= (-4;y-4)
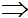
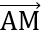 .
. 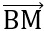 = 3.(-4) + (y-3).(y-4) = y2 - 7y
= 3.(-4) + (y-3).(y-4) = y2 - 7y
Tam giác MAB vuông tại M 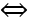
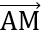 .
. 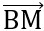 = 0
= 0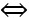 y2 - 7y = 0
y2 - 7y = 0
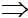 y(y-7) = 0
y(y-7) = 0
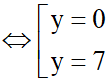
Vậy ta tìm được 2 điểm M thỏa mãn là M (0;0) hoặc M (0;7).
Dạng 8: Tìm giá trị lớn nhất, nhỏ nhất trong hình học.
Phương pháp giải:
- Tìm điểm M 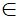 d sao cho MA + MB nhỏ nhất.
d sao cho MA + MB nhỏ nhất.
+) Khi A và B nằm khác phía đối với d. Tìm tọa độ tổng quát của M. Áp dụng bất đẳng thức trong tam giác, ta có: MA + MB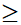 AB, dấu “=” xảy ra
AB, dấu “=” xảy ra 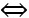 M, A, B thẳng hàng, từ đó tìm tọa độ M thích hợp.
M, A, B thẳng hàng, từ đó tìm tọa độ M thích hợp.
+) Khi A và B nằm cùng phía với d. Tìm tọa độ tổng quát của M. Tìm tọa độ điểm A’ là điểm đối xứng với A qua d. Áp dụng bất đẳng thức trong tam giác: MA' + MB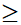 A'B. Dấu “=” xảy ra
A'B. Dấu “=” xảy ra 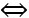 M, A’, B thẳng hàng, từ đó tìm tọa độ M thích hợp.
M, A’, B thẳng hàng, từ đó tìm tọa độ M thích hợp.
- Tìm điểm M 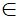 d sao cho |MA - MB| lớn nhất.
d sao cho |MA - MB| lớn nhất.
+) Khi A, B cùng phía đối với d: Tìm tọa độ tổng quát của M. Áp dụng bất đẳng thức trong tam giác, ta có: |MA - MB|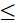 AB, dấu “=” xảy ra
AB, dấu “=” xảy ra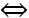 M, A, B thẳng hàng, từ đó tìm tọa độ M thích hợp.
M, A, B thẳng hàng, từ đó tìm tọa độ M thích hợp.
+) Khi A và B nằm khác phía với d. Tìm tọa độ tổng quát của M. Tìm tọa độ điểm A’ là điểm đối xứng với A qua d. Áp dụng bất đẳng thức trong tam giác: |MA' - MB|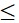 A'B
A'B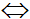 |MA-MB|
|MA-MB|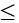 A'B. Dấu “=” xảy ra
A'B. Dấu “=” xảy ra 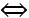 M, A’, B thẳng hàng, từ đó tìm tọa độ M thích hợp.
M, A’, B thẳng hàng, từ đó tìm tọa độ M thích hợp.
Ví dụ minh họa:
Bài 1: Cho điểm P thuộc trục hoành, A (1;1) và B (2;-4). Tìm P sao cho PA + PB nhỏ nhất.
Lời giải:
P thuộc trục hoành nên ta gọi P (x;0). A và B nằm về hai phía của trục hoành.
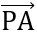 = (1-x;1)
= (1-x;1)
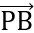 = (2-x;x-4)
= (2-x;x-4)
Áp dụng bất đẳng thức trong tam giác ta có:
PA + PB 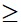 AB
AB
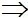 PA + PB nhỏ nhất khi dấu “=” xảy ra.
PA + PB nhỏ nhất khi dấu “=” xảy ra.
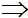 PA + PB = AB
PA + PB = AB
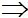 P, A, B thẳng hàng
P, A, B thẳng hàng
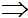
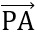 ,
, 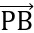 cùng phương
cùng phương
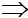
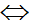 -4 + 4x = 2 - x
-4 + 4x = 2 - x
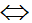 x =
x = 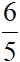
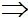 P
P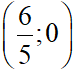
Bài 2: Cho tọa độ các điểm A (1;1) và B (-2;-4). Điểm M là điểm thuộc đường thẳng d: y = -x . Tìm M sao cho |MA-MB| lớn nhất.
Lời giải:
Điểm M là điểm thuộc đường thẳng d: y = -x nên ta gọi M = (x; -x).
Có A, B nằm về 2 phía của đường thẳng d. Gọi A’ (xA;yA) là điểm đối xứng của A qua d. Chọn điểm K (2;-2) thuộc đường thẳng d và H(xH;yH) là chân đường vuông góc hạ từ A xuống d nên ta có: AH  HK
HK 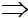
 .
.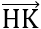 = 0.
= 0.
Ta có:
 = (1-xH;1+;yH)
= (1-xH;1+;yH)
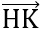 = (2-xH;-2+;yH)
= (2-xH;-2+;yH)
 .
.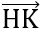 = 0
= 0 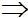 (1-xH)(2-xH) + (1+xH)(-2+xH) = 0
(1-xH)(2-xH) + (1+xH)(-2+xH) = 0
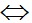 2x2 - 4x = 0
2x2 - 4x = 0
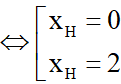
Loại x = 2 vì khi đó H trùng với K. Vậy ta chọn H (0;0).
Khi đó, H là trung điểm của AA’ nên ta có: 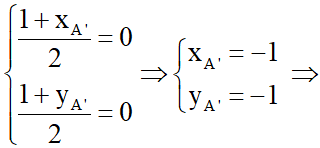 A’(-1;-1)
A’(-1;-1)
Ta có:
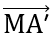 = (-1-x;-1+x)
= (-1-x;-1+x)
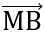 = (-2-x;-4+x)
= (-2-x;-4+x)
Áp dụng bất đẳng thức trong tam giác ta có:
|MA'-MB| 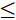 A'B
A'B 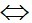 |MA-MB|
|MA-MB| 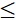 A'B
A'B
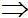 |MA-MB| lớn nhất khi và chỉ khi dấu “=” xảy ra.
|MA-MB| lớn nhất khi và chỉ khi dấu “=” xảy ra.
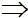 |MA'-MB| = A'B
|MA'-MB| = A'B
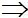 M, A’, B thẳng hàng.
M, A’, B thẳng hàng.
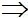
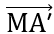 ,
, 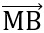 cùng phương.
cùng phương.
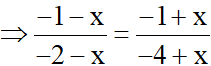
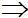 4 + 3x - x2 = 2 - x + x2
4 + 3x - x2 = 2 - x + x2
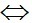 x =
x = 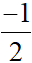
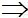 M
M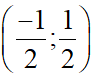
C. Bài tập vận dụng
Bài 1: Cho tam giác ABC vuông cân tại A, biết BC = a. Tính tích vô hướng 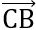 .
.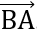 .
.
Đáp án: 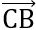 .
.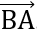 = -
= -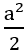
Bài 2: Cho hai vectơ 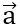 ,
, 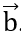 biết |
biết |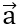 | = 5, |
| = 5, |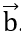 | = 6 và
| = 6 và 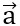 .
.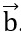 Tính góc (
Tính góc (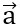 ,
,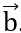 ).
).
Đáp án: (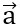 ,
,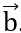 ) =
) = 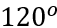
Bài 3: Cho hai điểm A (5;3), B (3;2) và I là trung điểm của AB. Tính độ dài AI.
Đáp án: AI = 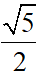
Bài 4: Cho tam giác ABC có A (2;3), B (1;4) và C (2;7). Biết M là trung điểm của BC. Tính độ dài AM.
Đáp án: AM = 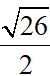
Bài 5: Cho tam giác ABC có A (10;5), B (3;2), C (6;-5). Chứng minh rằng tam giác ABC vuông tại B.
Đáp án: 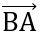 .
.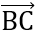 = 0
= 0 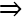 BA
BA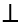 BC
BC 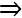 tam giác ABC vuông tại B.
tam giác ABC vuông tại B.
Bài 6: Cho hai vectơ 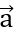 = (1;2) và
= (1;2) và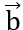 = (x;-1). Tìm x để độ dài của vectơ
= (x;-1). Tìm x để độ dài của vectơ 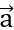 và độ dài của vectơ
và độ dài của vectơ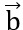 bằng nhau.
bằng nhau.
Đáp án: x = 2 hoặc x = -2.
Bài 7: Cho hình chữ nhật ABCD tâm O và M là điểm tùy ý. Chứng minh đẳng thức: 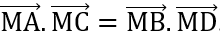 .
.
Đáp án: VP = 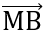 .
.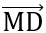 = (
= (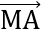 +
+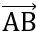 )(
)(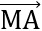 +
+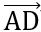 ) =
) = 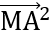 +
+ 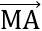 .
.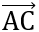 =
= 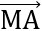 .
.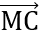 = VT
= VT
Bài 8: Cho hai điểm A và B. O là trung điểm của AB, M là điểm tùy ý. Chứng minh đẳng thức: 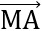 .
.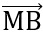 = OM2 - OA2
= OM2 - OA2
Đáp án: VT = ( +
+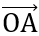 )(
)(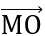 +
+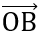 ) = MO +
) = MO + 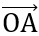 .
.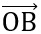 = OM2 - OA2 = VP
= OM2 - OA2 = VP
Bài 9: Cho vectơ 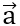 = (2;-3) , tìm tọa độ vectơ
= (2;-3) , tìm tọa độ vectơ 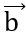 , biết cùng phương và
, biết cùng phương và 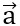 .
.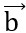 = -26
= -26
Đáp án: 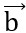 = (-4;6)
= (-4;6)
Bài 10: Cho A (5;-1) và B (-1;3). Tìm điểm P thuộc trục tung sao cho 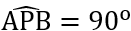 .
.
Đáp án: P (0;4) hoặc P (0;-2)
Bài 11: Cho tam giác ABC biết A (4;3), B (-3;3), C (2;-4). Tìm điểm K là chân đường cao kẻ từ C.
Đáp án: K (2;3)
Bài 12: Trong mặt phẳng Oxy, chứng minh tứ giác ABCD là hình vuông. Biết các tọa độ A (0;-2), B (5;0), C (3;5), D (-2;3).
Đáp án: Có AB = BC = CD = DA = 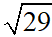 và
và 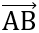 .
.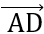 = 0
= 0 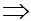 ABCD là hình vuôngBài 13: Cho ba điểm A (1;3), B (-1;-1), C (5;-4). Chứng minh rằng ba điểm nay tạo lập thành tam giác vuông.
ABCD là hình vuôngBài 13: Cho ba điểm A (1;3), B (-1;-1), C (5;-4). Chứng minh rằng ba điểm nay tạo lập thành tam giác vuông.
Đáp án: Có A,B,C không thẳng hàng và 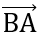 .
.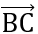 = 0
= 0  Tam giác ABC vuông tại B
Tam giác ABC vuông tại B
Bài 14: Cho 3 điểm A, B, M. Biết A (1;1), B (3;-2) và điểm M thuộc đường thẳng y = 2x. Tìm M để MA + MB nhỏ nhất.
Đáp án: M (1;2)
Bài 15: Cho hai điểm A (1;-2) và B (6;3). Tìm điểm N trên trục hoành sao cho |NA-NB| lớn nhất.
Đáp án: N (3;0)
D. Bài tập tự luyện
Câu 1: Cho hai vectơ:
Giá trị của tích vô hướng a→.b→ là:
A. 10 B. -10 C. 10√3 D. -10√3
A. 10 B. -10 C. 10√3 D. -10√3
Câu 3: Trong mặt phẳng tọa độ Oxy, cho A(2; 1), B(3; -2), C(5; 7). Giá trị của AB→.AC→ là
A. 15 B. 21 C. -15 D. -21
Câu 4: Cho các vectơ a→,b→ khác 0→. Khẳng định nào sau đây là đúng?
Câu 5: Cho tứ giác ABCD có hai đường chéo vuông góc với nhau. Biểu thức:
A. AB2
B. AC2
C. AD2
D. 0
Câu 6: Cho đoạn thẳng AB và điểm I là trung điểm của đoạn thẳng AB. M là một điểm bất kì. Khẳng định nào sau đây là đúng?
Câu 7: Cho tam giác ABC có AB = 2, AC = 4, góc A = 60o. M và N lần lượt là trung điểm của AB và AC. Biểu thức BN→.CM→ bằng
A. 5
B. -5
C. 7
D. -7
Câu 8: Độ dài của vectơ a→=(5;12) là
A. 17
B. 169
C. 13
D. √159
Câu 9: Cho hai vectơ a→=(1; √3),b→=(-2√3;6). Góc giữa hai vectơ a→ vàb→ l
A. 0o
B. 30o
C. 45o
D. 60o
Câu 10: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(0; 2), B(-2; 8), C(-3; 1). Tọa độ tâm đường tròn ngoại tiếp của tam giác ABC là
A. (5/2;-9/2) B. (-5/2;9/2) C. (-2;4) D.(-3;5)
Câu 11: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1; 1), B(4; 13), C(5; 0). Tọa độ trực tâm H của tam giác ABC là
A. (2; 2) B. (1; 1) C. (-2; -2) D. (-1; -1)
Câu 12: Cho hình chữ nhật ABCD có AB = 2, AD = 4, điểm M thuộc cạnh BC thỏa mãn BM = 1. Điểm N thuộc đường chéo AC thỏa mãn AN→ =xAC→. Giá trị của x để tam giác AMN vuông tại M là
A. 5/8 B. 5/4 C. 5/16 D. 0,5
Câu 13: Cho các vectơ a→,b→ khác 0→. Khẳng định nào sau đây là đúng?
Câu 14: Cho các vectơ a→,b→ thỏa mãn |a→|=8,|b→|=10,(a→,b→ )=30o. Giá trị của tích vô hướng a→.b→ là:
A. 40 B. -40√3 C. 40√3 D. -40
Câu 15: Cho các vectơ a→,b→ thỏa mãn |a→| = 4,|b→| = 6,(a,b→ ) = 120o. Giá trị của tích vô hướng a→.b→ là:
A. - 12 B. 12 C. 12√3 D. -12√3
Câu 16: Cho tam giác ABC đều cạnh a. Giá trị của AB→.AC→ là
A. a2 B. a2/2 C. -a2/2 D. 2a2
Câu 17: Cho các vectơ a→,b→. Khẳng định nào sau đây là đúng?
Câu 18: Cho các vectơ a→,b→. Khẳng định nào sau đây là đúng?
Câu 19: Cho các vectơ a→,b→ khác 0→. Khẳng định nào sau đây là đúng?
Xem các Phương pháp giải bài tập hay, chi tiết khác:
Công thức góc giữa hai vectơ chi tiết nhất
Công thức Tích vô hướng của hai vectơ chi tiết nhất
Các tính chất của tích vô hướng chi tiết nhất
Công thức tính độ dài vectơ chi tiết nhất
Công thức khoảng cách giữa hai điểm vectơ lớp 10
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.