Công thức khoảng cách giữa hai điểm vectơ (50 bài tập minh họa) HAY NHẤT 2024

Ngọc Nguyễn Ngày: 21-08-2023 Lớp 10

370

Toptailieu.vn biên soạn và giới thiệu Công thức khoảng cách giữa hai điểm vectơ (50 bài tập minh họa) HAY NHẤT 2024 gồm đầy đủ các phần: Lý thuyết, phương pháp giải, bài tập minh họa có lời giải chi tiết giúp học sinh làm tốt bài tập Toán 10 từ đó học tốt môn Toán. Mời các bạn đón xem:

Công thức khoảng cách giữa hai điểm vectơ (50 bài tập minh họa) HAY NHẤT 2024

I. Công thức tính khoảng cách

Khoảng cách giữa hai điểm $A (x_{A}; y_{A})$ và $B (x_{B}; y_{B})$ được tính theo công thức:

$A B = \sqrt{{(x_{B} - x_{A})}^{2} + {(y_{B} - y_{A})}^{2}}$ .

II. Ví dụ minh họa

Bài 1: Trong mặt phẳng Oxy, cho điểm A (1; 2) và điểm B (5; 3). Tính độ dài đoạn thẳng AB.

Lời giải:

Độ dài đoạn thẳng AB là:

$A B = \sqrt{{(5 - 1)}^{2} + {(3 - 2)}^{2}} = \sqrt{17}$

Bài 2: Cho tam giác ABC có các tọa độ A(3; 4) , B(5; 2) và C(3; 2). Tính độ dài các cạnh AB, AC, BC.

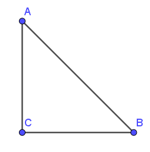
Công thức khoảng cách giữa hai điểm vectơ lớp 10 - Toán lớp 10 (ảnh 1)

Lời giải:

Độ dài các cạnh AB, AC, BC lần lượt là:

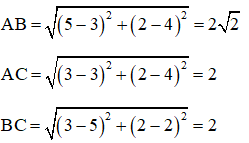
Công thức khoảng cách giữa hai điểm vectơ lớp 10 - Toán lớp 10 (ảnh 1)

Bài 3: Nhà bạn An ở điểm A(6; 7). Bạn An cần đi đến bệnh viện gần nhất để khám bệnh, coi đường đi luôn là đường thẳng. Có hai bệnh viện ở gần nhà An. Bệnh viện B ở điểm B(2; 3) và bệnh viện C ở điểm C(8; 9). Hỏi bệnh viện nào gần nhà An nhất.

Lời giải:

Coi các quãng đường A đến B và A đến C là đường thẳng.

Ta có:

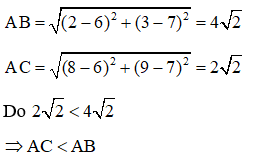
Công thức khoảng cách giữa hai điểm vectơ lớp 10 - Toán lớp 10 (ảnh 1)

Vậy bệnh viện C gần nhà An nhất.

III. Bài tập tự luyện

Câu 1. Cho 5 điểm M, N, P, Q, R. Tính tổng $\vec{M N} + \vec{P Q} + \vec{R N} + \vec{N P} + \vec{Q R}$ .

A. $\vec{M R}$ ;

B. $\vec{M N}$ ;

C. $\vec{P R}$ ;

D. $\vec{M P}$ .

Câu 2. Cho M, N, P lần lượt là trung điểm các cạnh AB, BC, CA của tam giác ABC. Hỏi vectơ $\vec{M P} + \vec{N P}$ bằng vectơ nào?

A. $\vec{A P}$ ;

B. $\vec{B P}$ ;

C. $\vec{M N}$ ;

D. $\vec{M B} + \vec{N B}$ .

Câu 3. Cho M, N, P, Q là bốn điểm tùy ý. Trong các hệ thức sau, hệ thức nào sai?

A. $\vec{M N} (\vec{N P} + \vec{P Q}) = \vec{M N} . \vec{N P} + \vec{M N} . \vec{P Q}$ ;

B. $\vec{M P} . \vec{M N} = - \vec{M N} . \vec{M P}$ ;

C. $\vec{M N} . \vec{P Q} = \vec{P Q} . \vec{M N}$ ;

D. $(\vec{M N} - \vec{P Q}) (\vec{M N} + \vec{P Q}) = M N^{2} - P Q^{2}$

Câu 4. Cho tam giác ABC có BC = a, CA = b, AB = c. Gọi M là trung điểm BC. Tính $\vec{A M} . \vec{B C}$ .

A. $\vec{A M} . \vec{B C} = \frac{b^{2} - c^{2}}{2}$ ;

B. $\vec{A M} . \vec{B C} = \frac{c^{2} + b^{2}}{2}$ ;

C. $\vec{A M} . \vec{B C} = \frac{c^{2} + b^{2} + a^{2}}{2}$ ;

D. $\vec{A M} . \vec{B C} = \frac{c^{2} + b^{2} - a^{2}}{2}$ .

Câu 5. Nếu $\vec{A B} = \vec{A C}$ thì

A. Tam giác ABC là tam giác cân;

B. Tam giác ABC là tam giác đều;

C. A là trung điểm của đoạn thẳng BC;

D. Điểm B trùng với điểm C.

Câu 6. Cho hình vuông ABCD tâm O. Tính tổng $(\vec{A B}, \vec{D C}) + (\vec{A D}, \vec{C B}) + (\vec{C O}, \vec{D C})$ .

A. 45°;

B. 405°;

C. 315°;

D. 225°.

Câu 7. Cho tam giác ABC. Gọi D, E, F lần lượt là trung điểm của các cạnh BC, CA, AB. Đẳng thức nào sau đây đúng?

A. $\vec{A D} + \vec{B E} + \vec{C F} = \vec{A B} + \vec{A C} + \vec{B C}$ ;

B. $\vec{A D} + \vec{B E} + \vec{C F} = \vec{A F} + \vec{C E} + \vec{B D}$ ;

C. $\vec{A D} + \vec{B E} + \vec{C F} = \vec{A E} + \vec{B F} + \vec{C D}$ ;

D. $\vec{A D} + \vec{B E} + \vec{C F} = \vec{B A} + \vec{B C} + \vec{A C}$ .

Câu 8. Cho hai vectơ không cùng phương $\vec{a}$ và $\vec{b}$ . Mệnh đề nào sau đây đúng?

A. Không có vectơ nào cùng phương với cả hai vectơ $\vec{a}$ và $\vec{b}$ ;

B. Có vô số vectơ cùng phương với cả hai vectơ $\vec{a}$ và $\vec{b}$ ;

C. Có một vectơ cùng phương với cả hai vectơ $\vec{a}$ và $\vec{b}$ , đó là $\vec{0}$ ;

D. Cả A, B, C đều sai.

Câu 9. Cho tam giác ABC và một điểm M tùy ý. Cho $\vec{v} = \vec{M A} + \vec{M B} - 2 \vec{M C}$ . Hãy xác định vị trí của điểm D sao cho $\vec{C D} = \vec{v}$ .

A. D là điểm thứ tư của hình bình hành ABCD;

B. D là điểm thứ tư của hình bình hành ACBD;

C. D là trọng tâm của tam giác ABC;

D. D là trực tâm của tam giác ABC.

Câu 10. Cho ba điểm phân biệt A, B, C. Khẳng định nào sau đây đúng?

A. $\vec{C A} - \vec{B A} = \vec{B C}$ ;

B. $\vec{A B} + \vec{A C} = \vec{B C}$ ;

C. $\vec{A B} + \vec{C A} = \vec{C B}$ ;

D. $\vec{A B} - \vec{B C} = \vec{C A}$ .

Câu 11. Cho tam giác ABC. Tập hợp các điểm M thỏa mãn $\vec{M A} . \vec{B C} = 0$ là:

A. một điểm;

B. đường thẳng;

C. đoạn thẳng;

D. đường tròn.

Câu 12. Cho tam giác ABC đều cạnh 2a. Đẳng thức nào sau đây là đúng?

A. $\vec{A B} = \vec{A C}$ ;

B. $\vec{A B} = 2 a$ ;

C. $(\vec{A B}) = 2 a$ ;

D. $\vec{A B} = A B$ .

Câu 13. Cho hình thoi ABCD tâm O và $\hat{B A D} = 60 °$ . Tính độ dài $\vec{A B} + \vec{A D}$ .

A. $(\vec{A B} + \vec{A D}) = 2 a \sqrt{3}$ ;

B. $(\vec{A B} + \vec{A D}) = a \sqrt{3}$ ;

C. $(\vec{A B} + \vec{A D}) = 3 a$ ;

D. $(\vec{A B} + \vec{A D}) = 3 a \sqrt{3}$ ;

Câu 14. Cho hai vectơ $\vec{a}$ và $\vec{b}$ khác $\vec{0}$ . Xác định góc α giữa hai vectơ $\vec{a}$ và $\vec{b}$ khi $\vec{a} . \vec{b} = - (\vec{a}) . (\vec{b})$ .

A. α = 180°;

B. α = 0°;

C. α = 90°;

D. α = 45°.

Câu 15. Cho hình vuông ABCD tâm O cạnh a. Gọi M là trung điểm AB, N là điểm đối xứng của C qua D. Hãy tính độ dài $\vec{M N}$ .

A. $(\vec{M N}) = \frac{a \sqrt{15}}{2}$ ;

B. $(\vec{M N}) = \frac{a \sqrt{5}}{3}$ ;

C. $(\vec{M N}) = \frac{a \sqrt{13}}{2}$ ;

D. $(\vec{M N}) = \frac{a \sqrt{5}}{4}$ .

Câu 16. Cho ba điểm phân biệt A, B, C. Nếu $\vec{A B} = - 3 \vec{A C}$ thì đẳng thức nào dưới đây đúng?

A. $\vec{B C} = - 4 \vec{A C}$ ;

B. $\vec{B C} = - 2 \vec{A C}$ ;

C. $\vec{B C} = 2 \vec{A C}$ ;

D. $\vec{B C} = 4 \vec{A C}$ .

Câu 17. Cho hình thoi ABCD có AC = 8 và BD = 6. Tính $\vec{A B} . \vec{A C}$ .

A. $\vec{A B} . \vec{A C}$ = 24;

B. $\vec{A B} . \vec{A C}$ = 26;

C. $\vec{A B} . \vec{A C}$ = 28;

D. $\vec{A B} . \vec{A C}$ = 32.

Câu 18. Mệnh đề nào sau đây sai?

A. Nếu M là trung điểm đoạn thẳng AB thì $\vec{M A} + \vec{M B} = \vec{0}$ ;

B. Nếu G là trọng tâm tam giác ABC thì $\vec{G A} + \vec{G B} + \vec{G C} = \vec{0}$ ;

C. Nếu ABCD là hình bình hành thì $\vec{C B} + \vec{C D} = \vec{C A}$ ;

D. Nếu ba điểm A, B, C phân biệt nằm tùy ý trên một đường thẳng thì $(\vec{A B}) + (\vec{B C}) = (\vec{A C})$ .

Câu 19. Cho lục giác đều ABCDEF tâm O. Đẳng thức nào sau đây sai?

A. $\vec{O A} + \vec{O C} + \vec{O E} = \vec{0}$ ;

B. $\vec{B C} + \vec{F E} = \vec{A D}$ ;

C. $\vec{O A} + \vec{O B} + \vec{O C} = \vec{E B}$ ;

D. $\vec{A B} + \vec{C D} = \vec{0}$ .

Câu 20. Cho tam giác ABC vuông tại A và AB = AC = a. Tính $\vec{A B} . \vec{B C}$ .

A. $\vec{A B} . \vec{B C} = - a^{2}$ ;

B. $\vec{A B} . \vec{B C} = a^{2}$ ;

C. $\vec{A B} . \vec{B C} = - \frac{a^{2} \sqrt{2}}{2}$ ;

D. $\vec{A B} . \vec{B C} = \frac{a^{2} \sqrt{2}}{2}$ .

Câu 21. Cho $\vec{a} \neq \vec{0}$ và điểm O. Gọi M, N lần lượt là hai điểm thỏa mãn $\vec{O M} = 3 \vec{a}$ và $\vec{O N} = - 4 \vec{a}$ . Tìm $\vec{M N}$ .

A. $\vec{M N} = 7 \vec{a}$ ;

B. $\vec{M N} = - 5 \vec{a}$ ;

C. $\vec{M N} = - 7 \vec{a}$ ;

D. $\vec{M N} = - 5 \vec{a}$ .

Câu 22. Cho $\vec{M N} \neq \vec{0}$ thì số vectơ cùng phương với vectơ đã cho là

A. 1;

B. 2;

C. 3;

D. Vô số.

Câu 23. Cho tam giác OAB vuông cân tại O với OA = OB = a. Độ dài của $\vec{u} = \frac{21}{4} \vec{O A} - \frac{5}{2} \vec{O B}$ là:

A. $\frac{a \sqrt{140}}{4}$ ;

B. $\frac{a \sqrt{321}}{4}$ ;

C. $\frac{a \sqrt{520}}{4}$ ;

D. $\frac{a \sqrt{541}}{4}$ .

Câu 24. Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC. Hỏi $\vec{M P} + \vec{N P}$ bằng vectơ nào trong các vectơ sau đây?

A. $\vec{A M}$ ;

B. $\vec{P B}$ ;

C. $\vec{A P}$ ;

D. $\vec{M N}$ .

Câu 25. Cho đường tròn (O). Từ điểm A nằm ngoài (O), kẻ hai tiếp tuyến AB, AC tới (O). Xét các mệnh đề sau:

(I) $\vec{A B} = \vec{A C}$

(II) $\vec{O B} = - \vec{O C}$

(III) $(\vec{B O}) = (\vec{C O})$

Mệnh đề đúng là:

A. Chỉ (I);

B. (I) và (III);

C. (I), (II), (III);

D. Chỉ (III).

Câu 26. Tập hợp các điểm M thỏa mãn $\vec{M B} (\vec{M A} + \vec{M B} + \vec{M C}) = 0$ với A, B, C là ba đỉnh của tam giác là

A. một điểm;

B. đường thẳng;

C. đoạn thẳng;

D. đường tròn.

Câu 27. Cho hình chữ nhật ABCD, biết AB = 4a, AD = 3a. Tính độ dài $\vec{A B} + \vec{A D}$ .

A. 7a;

B. 6a;

C. $2 a \sqrt{3}$ ;

D. 5a.

Câu 28. Cho tứ giác ABCD. Có bao nhiêu vectơ khác vectơ-không có điểm đầu và điểm cuối là các đỉnh của tứ giác?

A. 4;

B. 8;

C. 10;

D. 12.

Câu 29. Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm AB, CD. Khi đó $\vec{A C} + \vec{B D}$ bằng

A. $\vec{M N}$ ;

B. $2 \vec{M N}$ ;

C. $3 \vec{M N}$ ;

D. $- 2 \vec{M N}$ .

Câu 30. Cho hai lực $\vec{F_{1}}$ và $\vec{F_{2}}$ cùng tác động vào một vật đứng tại điểm O, biết hai lực $\vec{F_{1}}$ và $\vec{F_{2}}$ đều có cường độ là 50 (N) và chúng hợp với nhau một góc 60°. Hỏi vật đó phải chịu một lực tổng hợp có cường độ bằng bao nhiêu?