Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Tất tần tật về Định lí Sin (50 bài tập minh họa) HAY NHẤT 2024 gồm đầy đủ các phần: Lý thuyết, phương pháp giải, bài tập minh họa có lời giải chi tiết giúp học sinh làm tốt bài tập Toán 10 từ đó học tốt môn Toán. Mời các bạn đón xem:
Phương pháp giải Tất tần tật về Định lí Sin (50 bài tập minh họa) HAY NHẤT 2024
I. Công thức
- Định lí sin: Cho tam giác ABC bất kì, R là bán kính của đường tròn ngoại tiếp tam giác ABC.
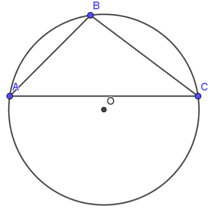
Ta có:
II. Ví dụ minh họa
Bài 1: Cho tam giác nhọn ABC có BC = 8cm, AB = 7cm và . Tính số đo góc .
Lời giải:
Xét tam giác nhọn ABC
Áp dụng định lí Sin ta có:
(cm)
Vì ABC là tam giác nhọn .
Bài 2: Cho tam giác ABC cân tại B có BC = 6cm và . Tính độ dài bán kính đường tròn ngoại tiếp của tam giác ABC.
Lời giải:
Xét tam giác ABC:
Gọi bán kính đường tròn ngoại tiếp của tam giác ABC là R
Áp dụng định lí Sin ta có:
(cm)
Bài 3: Cho tam giác ABC có AC = 4cm, và . Tìm độ dài BC.
Lời giải:
Xét tam giác ABC:
Có:
Áp dụng định lý Sin ta có:
(cm)
III. Bài tập tự luyện
Câu 1. Cho tam giác ABC có AB = c, BC = a và AC = b. Gọi R là bán kính đường tròn ngoại tiếp tam giác ABC. Trong các mệnh đề sau, mệnh đề nào sai?
A.
B. .
C. b = 2R.sinA;
D. c = 2R.sinC.
Câu 2. Cho tam giác ABC bất kì có BC = a, AC = b và AB = c. Công thức tính diện tích tam giác ABC nào sau đây là đúng:
A. S = bc.sinA;
B. S = ac.sinA;
C. S = bc.sinB;
D. S = ab.sinB.
Câu 3. Cho tam giác ABC bất kì có BC = a, AC = b và AB = c. Gọi ha, hb, hc độ dài các đường cao lần lượt ứng với các cạnh BC, CA, AB. Biết tam giác ABC có diện tích là S. Khẳng định nào sau đây là đúng?
A. ha =
B. hb =
C. hc =
D. ha =
Câu 4. Cho tam giác ABC bất kì có BC = a, AC = b và AB = c. Gọi R, r lần lượt là bán kính đường tròn ngoại tiếp và nội tiếp tam giác; p, S lần lượt là nửa chu vi và diện tích tam giác. Khẳng định nào sau đây là đúng?
A. S = abc;
B.
C.
D.
Câu 5: Cho tam giác ABC. Nếu a = 2b thì
A. hb = 2ha B. hb = ha C. a =2hb D. hb = 4ha
Câu 6: Cho tam giác ABC có a = BC, b = CA, c = AB, a + b = 2c. Khẳng định nào sau đây đúng?
A. sin B + sin C = 2 sin A
B. sin C + sin A = 2 sin B
C. sin A + sin B = 2 sin C
D. sin A + sin B = sin C
Câu 7: Cho tam giác ABC có a = BC, b = CA, c = AB, ab=c2. Khẳng định nào sau đây đúng?
A. sinAsinB= sin2C
B. sinAsinB= 2sin2C
C. sinAsinB= 4sin2C
D. 2sinAsinB= sin2C
Câu 8: Cho tam giác ABC có a = BC, b = CA, c = AB. Khẳng định nào sau đây sai?
A. sinB + sinC > sinA
B. sinC + sinA > sinB
C. sinA + sinB > sinC
D. sinA + sinB ≤ sinC
Câu 9: Một đa giác đều có góc ở mỗi đỉnh bằng α và nội tiếp đường tròn bán kính R thì có độ dài mỗi cạnh là:
A. R sinα B. 2Rcosα/2 C. Rcosα/2 D. 2R sinα
Câu 10: Cho tam giác ABC. Khẳng định nào sau đây đúng?
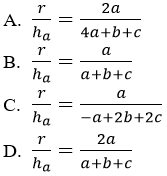
Câu 11: Cho tam giác ABC. Khẳng định nào sau đây là đúng?
A. ha = R sinB.sinC
B. ha = 4Rsin B.sinC
C. ha = 2Rsin B.sinC
D. ha = (1/4)Rsin B.sinC
Câu 12: Cho tam giác nhọn ABC nội tiếp (O; R). Diện tích của tam giác ABC bằng
A. (1/2)R2(sin2A + sin2B + sin2C)
B. (1/2)R2(sinA + sinB + sinC)
C. R2(sin2A + sin2B + sin2C)
D. R2(sinA + sin B + sinC)
Câu 13: Cho tam giác BC. M và N lần lượt thuộc hai tia AB và AC (M, N khác A). Khẳng định nào sau đây là đúng?
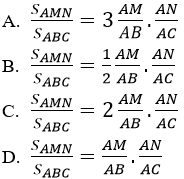
Câu 14: Cho tam giác ABC có a = BC, b = CA, c = AB. Khẳng định nào sau đây đúng?
A. a = b.cos B + c.cos C
B. a = b.cosC + c.cosB
C. a = b.sinB + c.sinC
D. a = b.sinC + c.sinB
Câu 15: Cho các vectơ a→ ,b→ khác 0→. Khẳng định nào sau đây là đúng?
Xem các Phương pháp giải bài tập hay, chi tiết khác:
Các công thức tính diện tích tam giác đầy đủ, chi tiết nhất
Hệ trục tọa độ trong mặt phẳng và cách giải bài tập
Phương trình đường thẳng và cách giải bài tập
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.