Toptailieu.vn biên soạn và giới thiệu Công thức viết phương trình đường phân giác (50 bài tập minh họa) HAY NHẤT 2024 gồm đầy đủ các phần: Lý thuyết, phương pháp giải, bài tập minh họa có lời giải chi tiết giúp học sinh làm tốt bài tập Toán 10 từ đó học tốt môn Toán. Mời các bạn đón xem:
Công thức viết phương trình đường phân giác (50 bài tập minh họa) HAY NHẤT 2024
I. Lý thuyết tổng hợp
- Tia phân giác của một góc: Là tia nằm giữa hai cạnh của góc và tạo với hai cạnh đó hai góc bằng nhau.
- Đường phân giác của một góc: Là đường thẳng chứa tia phân giác của góc đó
- Tính chất: Mọi điểm nằm trên đường phân giác của một góc đều cách đều hai cạnh của góc đó, tức là khoảng cách từ điểm M bất kì nằm trên đường phân giác của một góc đến hai cạnh của góc là bằng nhau.
II. Các công thức
- Công thức viết phương trình đường phân giác của góc tạo bởi hai đường thẳng: Cho hai đường thẳng và . Phương trình các đường phân giác của góc tạo bởi 2 đường thẳng đó là:
- Chú ý: Cho đường thẳng d: ax + by + c = 0 và hai điểm và không thuộc d.
Đặt f(x; y) = ax + by + c
+ Nếu A và B nằm cùng một phía đối với d.
+ Nếu A và B nằm khác phía đối với d.
III. Ví dụ minh họa
Bài 1: Cho hai đường thẳng d: x + 2y + 3 = 0 và d’: 2x + y + 3 = 0. Viết phương trình các đường phân giác của các góc tạo bởi d và d’.
Lời giải:
Phương trình các đường phân giác của các góc tạo bởi d và d’ là:
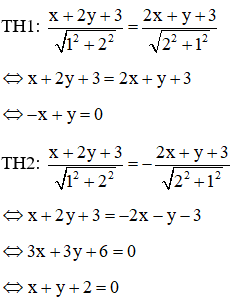
Vậy các phương trình đường phân giác của các góc tạo bởi hai đường thẳng d và d’ là và
Bài 2: Cho hai đường thẳng d: x - 2y + 1 = 0 và d’: 2x - y + 2 = 0. Viết phương trình các đường phân giác của các góc tạo bởi d và d’.
Lời giải:
Phương trình các đường phân giác của các góc tạo bởi d và d’ là:
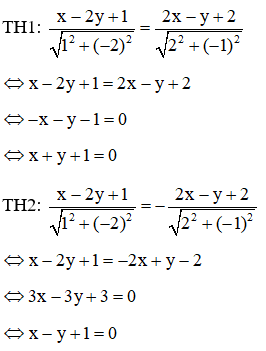
Vậy các phương trình đường phân giác của các góc tạo bởi hai đường thẳng d và d’ là và .
Bài 3: Cho tam giác ABC có đường thẳng chứa cạnh AB là d: 2x - y + 4 = 0, đường thẳng chứa cạnh AC là d’: x - 2y - 6 = 0 và hai điểm B, C thuộc Ox. Viết phương trình phân giác ngoài của góc .
Lời giải:
Phương trình đường phân giác của các góc tạo bởi d và d’ là:
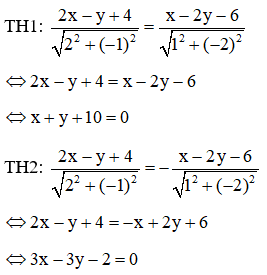
Do hai điểm B và C thuộc Ox và lần lượt thuộc d và d’ nên tọa độ hai điểm đó là : B(-2; 0) và C(6; 0).
Xét vị trí của hai điểm B và C đối với đường thẳng x + y + 10 = 0.
Ta có : (-2 + 0 + 10).( 6 + 0 + 10) > 0 nên hai điểm B và C nằm cùng phía so với đường thẳng x + y + 10 = 0.
Suy ra đường thẳng x + y + 10 = 0 là đường phân giác ngoài của góc .
IV. Bài tập vận dụng
Bài 1: Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(0; 2) , B( 1; 2) và C(3; 6 ) . Phương trình đường phân giác trong của góc A là:
A. 2x + y - 2 = 0 B. x - 2y + 4 = 0 C. 2x + y - 4 = 0 D. Đáp án khác
Lời giải
+ Ta viết phương trình đường thẳng AB và AC:
Đường thẳng AB :
⇒ ( AB) : 0(x - 0) + 1(y - 2) = 0 hay y - 2 = 0
Đường thẳng AC :
⇒ ( AC) : 4(x - 0) – 3(y - 2) = 0 hay 4x - 3y + 6 = 0
Suy ra các đường phân giác góc A là:
⇔ |4x - 3y + 6| = 5|y - 2|
Đặt f( x; y) = x - 2y + 4
⇒ f( B).f( C) =( 1 - 2.2 + 4) ( 3 - 2.6 + 4) = -5 < 0
⇒ B và C nằm khác phía so với đường thẳng : x - 2y + 4 = 0.
suy ra đường phân giác trong góc A là x - 2y + 4 = 0
Chọn B.
Bài 2: Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A( 1; 5) ; B( -4; -5) và C( 4; -1) . Phương trình đường phân giác ngoài của góc A là:
A. y + 5 = 0 B. y - 5 = 0 C. x + 1 = 0 D. x - 1 = 0
Lời giải
+ Ta viết phương trình đường thẳng AB và AC:
Đường thẳng AB :
⇒ ( AB) : 2( x - 1) – 1.( y - 5) = 0 hay 2x - y + 3 = 0
Đường thẳng AC :
⇒ ( AC) : 2( x - 1) + 1( y - 5) = 0 hay 2x + y - 7 = 0
Suy ra các đường phân giác góc A là:
⇔ |2x - y + 3| = |2x + y - 7|
⇔
Đặt f( x; y) = y - 5
⇒ f(B).f(C) = ( -5 - 5).( -1 - 5) = 60 > 0
⇒ B và C nằm cùng phía so với đường thẳng : y - 5 = 0.
suy ra đường phân giác ngoài góc A là y - 5 = 0
Chọn B.
Bài 3: Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng d1: 3x - 4y - 3 = 0 và d2 : 12x + 5y - 12 = 0. Phương trình đường phân giác góc nhọn tạo bởi hai đường thẳng d1 và d2 là:
A. 3x + 11y - 3 = 0 B. 11x - 3y - 11 = 0 C. 3x - 11y - 3 =0 D. 11x + 3y - 11 = 0
Lời giải
Các đường phân giác của các góc tạo bởi hai đường thẳng d1 và d2 là:
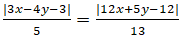
Gọi I là giao điểm của d1 và d2; tọa độ I là nghiệm hệ
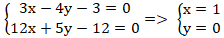
+ Gọi đường thẳng d: 3x + 11y - 3 = 0. Lấy điểm M(-10; 3) thuộc đường thẳng d.
Gọi H là hình chiếu của M lên d1.
Ta có: IM = 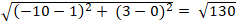
MH = d(M;d1 ) = 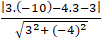
Suy ra
Suy ra d: 3x + 11y - 3 = 0 là đường phân giác góc tù nên đường phân giác góc nhọn là 11x - 3y - 11 = 0.
Chọn B.
Bài 4: Cho đường thẳng d: 3x + 4y – 5 = 0 và 2 điểm A( 1; 3) ; B( 2; m) . Tìm m để A và B nằm cùng phía đối với d?
A. m < 0 B. m > - 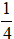
Hướng dẫn giải
Hai điểm A và B nằm về hai phía của đường thẳng d khi và chỉ khi:
( 3 + 12 - 5)( 6 + 4m - 5) < 0 hay m > -
Chọn B.
V. Bài tập tự luyện
Câu 1: Cho tam giác ABC có phương trình các cạnh AB: x + y - 1 = 0;
AC: 7x - y + 2 = 0 và BC: 10x + y - 19 = 0. Viết phương trình đường phân giác trong góc A của tam giác ABC.
A. 12x + 4y - 3 = 0 B. 2x + 6y + 7 = 0 C. 12x + 6y - 7 = 0 D. 2x - 6y +7 = 0
Lời giải:
Đáp án: D
+ AB và BC giao nhau tại B nên tọa độ của B là nghiệm hệ :
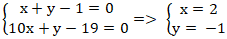
+ AC và BC cắt nhau tại C nên tọa độ C là nghiệm hệ:
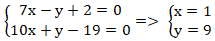
+ Phương trình các đường phân giác góc A là:
Đặt f1( x; y) = 2x - 6y + 7 ta có f1(B) . f1( C) < 0
Suy ra B và C nằm khác phía so với d1 và cùng phía so với d2.
Vậy phương trình đường phân giác trong góc A là: 2x - 6y + 7 = 0
Câu 2: Cho tam giác ABC có A(-2; -1); B(-1; 3) và C( 6; 1).Viết phương trình đường phân giác ngoài góc A của tam giác ABC.
A. x - y + 1 = 0 B. 5x + 3y + 9 = 0 C. 3x + 3y - 5 = 0 D. x + y + 3 = 0
Lời giải:
Đáp án: D
+ Phương trình đường thẳng AB:
⇒ Phương trình AB: 4( x + 2) – 1( y + 1) = 0 hay 4x - y + 7 = 0
+ Phương trình đường thẳng AC:
⇒ Phương trình AC: 1( x + 2) - 4( y + 1) = 0 hay x - 4y – 2 = 0
+ Phương trình các đường phân giác góc A là:
Đặt f1( x; y) = x + y + 3 ta có: f1(B).f1(C) > 0
Suy ra B và C nằm cùng phía so với d1 và khác phía so với d2.
Vậy phương trình đường phân giác ngoài góc A là: x + y + 3 = 0.
Câu 3: Cặp đường thẳng nào dưới đây là phân giác của các góc hợp bởi đường thẳng
∆: x + y = 0 và trục hoành Ox.
A. (1 + √2)x + y = 0 ; x - (1 - √2)y = 0 . B. (1 + √2)x + y = 0; x + (1 - √2)y = 0 .
C. (1 + √2)x - y = 0; x + (1 - √2)y = 0 . D. Tất cả sai
Lời giải:
Đáp án: D
Gọi M(x; y) là điểm thuộc đường phân giác
Theo đầu bài ta có: d( M; ∆) = d( M; Ox)
⇒ 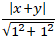
⇔
Câu 4: Cặp đường thẳng nào dưới đây là phân giác của các góc hợp bởi 2 đường thẳng ∆1: x + 2y - 3 = 0 và ∆2: 2x - y + 3 = 0 .
A. 3x + y = 0 và x - 3y = 0 . B. 3x + y = 0 và x + 3y - 6 = 0.C. 3x + y = 0 và – x + 3y - 6 = 0. D. 3x + y + 6 = 0 và x - 3y - 6 = 0.
Lời giải:
Đáp án: C
Gọi M(x; y) là điểm thuộc đường phân giác
⇒ d(M; ∆1) = d(M; ∆2) ⇒
⇒ x + 2y - 3 = ±(2x - y + 3) ⇒
Câu 5: Cho hai đường thẳng d : x + 2y + 3 = 0 và d’ : 2x + y + 3 = 0. Phương trình các đường phân giác của các góc tạo bởi d và d’ là
A. x + y = 0 ; x - y + 2 = 0 B. x - y = 0 ; x + y + 2 = 0
C. x + y + 2 = 0 ; x - y = 0 D. x + y - 2 = 0 ; x - y - 1 = 0
Lời giải:
Đáp án: C
Ta có: M(x ; y) thuộc đường phân giác khi và chỉ khi :
d(M; d) = d(M; d') ⇔
⇔ |x + 2y + 3| = |2x + y + 3| ⇔
Câu 6: Cho tam giác ABC có A(1; -2); B( 2; 2) và C(5; -3). Viết phương trình đường phân giác trong xuất phát từ đỉnh A của tam giác ABC?
A. 5x + 3y + 1 = 0 B. 3x + 2y + 1 = 0 C. x + y + 1 = 0 D. 5x + 2y - 1 = 0
Lời giải:
Đáp án: A
+Ta có: AB =
AC =
⇒ AB = AC nên tam giác ABC cân tại A.
⇒ Đường phân giác trong xuất phát từ A đồng thời là đường trung tuyến.
+ Gọi M là trung điểm BC; tọa độ M :
+ Đường thẳng AM:
⇒ Phương trình AM: 5( x - 1) + 3( y + 2) = 0 hay 5x + 3y + 1 = 0
Câu 7: Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(2; -1) ; B( -1;3) và C( 4; -1) . Phương trình đường phân giác ngoài của góc A là:
A. y + 5 = 0 B. x + 2y = 0 C. x + 1 = 0 D. 2x - y - 5 = 0
Lời giải:
Đáp án: B
+ Ta viết phương trình đường thẳng AB và AC:
Đường thẳng AB :
⇒ ( AB) : 4(x - 2) + 3( y + 1) = 0 hay 4x + 3y - 5 = 0
Đường thẳng AC :
⇒ ( AC) : 0(x - 2) + 1( y + 1) = 0 hay y + 1 = 0
Suy ra các đường phân giác góc A là:
⇔ |4x + 3y - 5| = 5|y + 1|
⇔
Đặt f( x; y) = 2x - y - 5
⇒ f( B).f( C) = (- 2 - 3 - 5).( 2.4 + 1 - 5) = -40 < 0
⇒ B và C nằm khác phía so với đường thẳng 2x - y - 5 = 0
suy ra đường phân giác ngoài góc A là x + 2y = 0
Xem các Phương pháp giải bài tập hay, chi tiết khác:
Công thức về vị trí tương đối của hai đường thẳng hay và chi tiết nhất
Công thức tính góc giữa hai đường thẳng hay, chi tiết nhất
Công thức tính khoảng cách từ một điểm đến một đường thẳng
Công thức xác định khoảng cách giữa hai đường thẳng song song
Công thức xác định tâm và bán kính của đường tròn hay, chi tiết nhất
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.