Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Cách giải phương trình, bất phương trình tổ hợp (HAY NHẤT 2024) gồm đầy đủ các phần: Lý thuyết, phương pháp giải, bài tập minh họa có lời giải chi tiết giúp học sinh làm tốt bài tập Toán 11 từ đó học tốt môn Toán. Mời các bạn đón xem:

Phương pháp giải Cách giải phương trình, bất phương trình tổ hợp (HAY NHẤT 2024)

1. Lý thuyết

- Hoán vị của n phần tử: P_n = n! = n(n – 1)(n – 2)…3.2.1.

- Chỉnh hợp chập k của n ($0\le k\le n$): $A_n^k=\frac{n!}{(n-k)!}$

- Tổ hợp chập của n ($0\le k\le n$): $C_n^k=\frac{n!}{(n-k)!k!}=\frac{A_n^k}{k!}$

- Tính chất của tổ hợp:

$\begin{array}{l}{C}_n^k=C_n^{n-k},(0\le k\le n)\\ C_{n+1}^{k+1}=C_n^k+C_n^{k+1},(1\le k\le n)\end{array}$

2. Phương pháp giải

Sử dụng công thức hoán vị, chỉnh hợp, tổ hợp đưa về các phương trình, bất phương trình đã học và giải quyết.

3. Ví dụ minh họa

Ví dụ 1. Giải phương trình:

a) $2A_x^2=C_x^{x-1}+23x$

b) $3A_n^2-A_{2n}^2+42=0$

c) $C_{x+1}^{x-2}+2C_{x-1}^3=7(x-1)$

Lời giải

a) $2A_x^2=C_x^{x-1}+23x$

Điều kiện: $\left\{\begin{array}{l}x\ge 2\\ x\in \mathbb{N}\end{array}\right.$

Phương trình trên tương đương với:

$2\frac{x!}{(x-2)!}=\frac{x!}{(x-1)!.1!}+23x$

$\begin{array}{l}\iff 2x\left(x-1\right)=x+23x\\ \iff 2x^2-2x-24x=0\\ \iff 2x^2-26x=0\\ \iff x^2-13x=0\\ \iff \left[\begin{array}{l}x=0\left(Loại\right)\\ x=13\end{array}\right.\end{array}$

Vậy nghiệm của phương trình là x = 13.

b) $3.A_n^2-A_{2n}^2+42=0$

Điều kiện: $\left\{\begin{array}{l}n\ge 2\\ n\in \mathbb{N}\end{array}\right.$

Phương trình trên tương đương với

$\begin{array}{l}3\frac{n!}{(n-2)!}-\frac{\left(2n\right)!}{(2n-2)!}+42=0\\ \iff 3n(n-1)-2n(2n-1)+42=0\\ \iff 3n^2-3n-4n^2+2n+42=0\\ \iff -n^2-n+42=0\\ \iff -\left(n+7\right)\left(n-6\right)=0\\ \iff \left[\begin{array}{l}n=6\\ n=-7\left(Loại\right)\end{array}\right.\end{array}$

Vậy nghiệm của phương trình là: n = 6.

c) $C_{x+1}^{x-2}+2C_{x-1}^3=7(x-1)$

Điều kiện: $\left\{\begin{array}{l}x-1\ge 3\\ x\in \mathbb{N}\end{array}\right.\iff \left\{\begin{array}{l}x\ge 4\\ x\in \mathbb{N}\end{array}\right.$

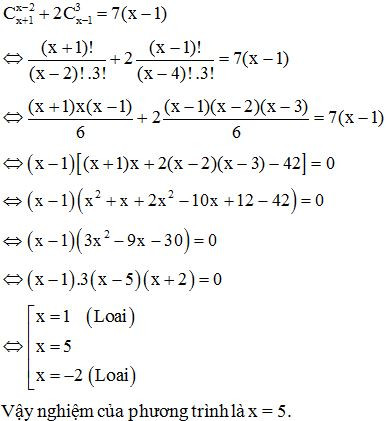
Ví dụ 2: Giải bất phương trình

a) $A_n^3+15<15n$

b) $A_n^3<A_n^2+12$

Lời giải

a) Điều kiện: $n\ge 3,n\in \mathbb{N}$

Ta có: $A_n^3+15<15n$

$\begin{array}{l}\iff \frac{n!}{(n-3)!}+15-15n<0\\ \iff n(n-1)(n-2)-15(n-1)<0\\ \iff (n-1)\left(n^2-2n-15\right)<0\\ \iff (n-1)(n+3)(n-5)<0\end{array}$

Vì  nên n – 1 > 0 và n + 3 > 0

Kết hợp với điều kiện, ta có n = 3 và n = 4 thỏa mãn.

Vậy nghiệm của bất phương trình: n = 3; n = 4.

b) Điều kiện: $n\ge 3,n\in N$.

$\begin{array}{l}{A}_n^3<A_n^2+12\\ \iff \frac{n!}{\left(n-3\right)!}<\frac{n!}{\left(n-2\right)!}+12\\ \iff n(n-1)(n-2)<n(n-1)+12\\ \iff n^3-3n^2+2n<n^2-n+12\\ \iff n^3-4n^2+3n-12<0\\ \iff (n-4)\left(n^2+3\right)<0\\ \iff n<4\end{array}$

Kết hợp với điều kiện, ta có n = 3 thỏa mãn.

Vậy nghiệm của bất phương trình: n = 3.

Ví dụ 3. Một đa giác có số đường chéo gấp đôi số cạnh. Hỏi đa giác đó có bao nhiêu cạnh?

Lời giải

Gọi số đỉnh của đa giác là n. Điều kiện: $n\in \mathbb{N}$ và $n>3$.

Vậy số cạnh của đa giác cũng là n.

Số đoạn thẳng có hai đầu mút từ n đỉnh trên là $C_n^2$ đoạn thẳng

Do đó số đường chéo của đa giác là $C_n^2-n$.

Theo giả thiết, số đường chéo gấp đôi số cạnh nên ta có:

$\begin{array}{l}{C}_n^2-n=2n\\ \iff \frac{n!}{2!.(n-2)!}=3n\\ \iff \frac{n(n-1)}{2}=3n\\ \iff n^2-n=6n\\ \iff n^2-7n=0\\ \iff \left[\begin{array}{l}n=0\left(Loại\right)\\ n=7\end{array}\right.\end{array}$

Vậy đa giác có 7 cạnh.

4. Bài tập vận dụng

Câu 1. Nghiệm của phương trình: $C_n^3=10$ là

A. 6

B. 5

C. 3

D. 4

Câu 2. Tập hợp tất cả nghiệm thực của phương trình $A_x^2-A_x^1=3$ là

A.{-1}

B. {3}

C.{-1;3}

D.{1}

Câu 3. Nghiệm của phương trình $A_x^3+C_x^{x-2}=14x$ là

A. Một số khác

B. x = 6

C. x = 5 

D. x = 4

Câu 4. Tìm tập nghiệm của phương trình $C_x^2+C_x^3=4x$.

A.{0}

B.{-5; 5}

C.{5}

D.{-5; 0; 5}

Câu 5. Cho số tự nhiên n thỏa mãn $C_n^2+A_n^2=9n$. Mệnh đề nào sau đây là đúng?

A. n chia hết cho 7

B. n chia hết cho 5

C. n chia hết cho 2

D. n chia hết cho 3

Câu 6. Nghiệm của phương trình $A_x^{10}+A_x^9=9A_x^8$ là

A. x = 5

B. x = 11

C. x = 11; x = 5

D. x = 10; x = 2

Câu 7. Tổng của tất cả các số tự nhiên n thỏa mãn $\frac{1}{C_n^1}-\frac{1}{C_{n+1}^2}=\frac{7}{6C_{n+4}^1}$ là

A. 13

B. 11

C. 10

D. 12

Câu 8. Tính tổng tất cả các số nguyên dương n thỏa mãn $A_n^2-3C_n^2=15-5n$

A. 13

B. 10

C. 12

D. 11

Câu 9. Cho n là số nguyên dương thỏa mãn $A_n^2=C_n^2+C_n^1+4n+6$. Hệ số của số hạng chứa x⁹ của khai triển biểu thức $P\left(x\right)={\left(x^2+\frac{3}{x}\right)}^n$ bằng

A. 18564

B. 64152

C. 192456

D. 194265

Câu 10. Tìm hệ số của số hạng chứa x⁸ trong khai triển nhị thức Niu tơn của ${\left(\frac{n}{2x}+\frac{x}{2}\right)}^{2n}\left(x\ne 0\right)$, biết số nguyên dương n thỏa mãn $C_n^3+A_n^2=50$.

A. $\frac{29}{51}$

B. $\frac{297}{512}$

C. $\frac{97}{12}$

D. $\frac{279}{215}$

Câu 11. Nghiệm của bất phương trình (ẩn n thuộc tập số tự nhiên) $\frac{C_{n+1}^2}{C_n^2}\ge \frac{3}{10}n$ là

A. $0\le n\le 2$

B. $1\le n\le 5$

C. $2\le n\le 5$

D. $2\le n<4$

Câu 12. Nghiệm của bất phương trình (ẩn n thuộc tập số tự nhiên) $A_{n+1}^3+C_{n+1}^{n-1}<14(n+1)$ là

A. $2\le n\le 5$

B. $0\le n\le 2$

C. $1\le n\le 5$

D. $2\le n<4$

Câu 13. Nghiệm của phương trình (ẩn n thuộc tập số tự nhiên) $C_{n+2}^{n-1}+C_{n+2}^n>\frac{5}{2}{A}_n^2$ là

A. $n\ge 2$

B. $n\ge 3$

C. $n\ge 5$

D. $n\ge 4$

Câu 14. Nghiệm bất phương trình sau: $\frac{1}{2}{A}_{2x}^2-A_x^2\le \frac{6}{x}{C}_x^3+10$ là

A. x = 3; x = 4

B. x = 3

C. x = 2; x = 3; x = 4

D. x = 4

Câu 15. Trên đường thẳng d₁ cho 5 điểm phân biệt, trên đường thẳng d₂ song song với đường thẳng d₁, cho n điểm phân biệt. Biết có tất cả 175 tam giác được tạo thành mà 3 đỉnh lấy từ n + 5 điểm trên. Giá trị của n là

A. 10

B. 7

C. 8

D. 9

5. Bài tập tự luyện 

Bài 1:

Lời giải:

Bài 2:

Lời giải:

Bài 3: Cho đa giác đều n đỉnh, n ∈ N và n ≥ 3. Tìm n biết rằng đa giác đã cho có 135 đường chéo.

Lời giải:

Bài 4: Giải phương trình sau: P_x = 120

Lời giải:

Ta có: P_x = 120

Với x > 5 ⇒ P_x > P₅ = 120 ⇒ phương trình vô nghiệm

Với x < 5 ⇒ P_x < P₅ = 120 ⇒ phương trình vô nghiệm

Vậy x = 5 là nghiệm duy nhất.

Bài 5: Giải bất phương trình (ẩn n thuộc tập số tự nhiên)

Lời giải:

Với x ≥ 2,n ∈ N ta có:

Vậy nghiệm của bất phương trình n ≥ 2,n ∈ N.

Xem thêm Phương pháp giải các dạng bài tập hay, chi tiết khác:

Xác định biến cố và tính xác suất của biến cố chi tiết nhất

Trọn bộ công thức tính xác suất đầy đủ, chi tiết nhất

Công thức hoán vị

Công thức chỉnh hợp

Công thức tổ hợp