Toptailieu.vn biên soạn và giới thiệu Công thức tổ hợp (50 bài tập minh họa) HAY NHẤT 2024 gồm đầy đủ các phần: Lý thuyết, phương pháp giải, bài tập minh họa có lời giải chi tiết giúp học sinh làm tốt bài tập Toán 11 từ đó học tốt môn Toán. Mời các bạn đón xem:

Công thức tổ hợp (50 bài tập minh họa) HAY NHẤT 2024

1. Tổng hợp lý thuyết

Cho tập hợp A có n phần tử và cho số nguyên k, ($1\le k\le n$). Mỗi tập hợp con của A có k phần tử được gọi là một tổ hợp chập k của n phần tử của A.

- Số các tổ hợp chập k của một tập hợp có n phần tử là: $C_n^k=\frac{n!}{(n-k)!k!}=\frac{A_n^k}{k!}$.

- Tính chất:

$\begin{array}{l}{C}_n^0=C_n^n=1\\ C_n^k=C_n^{n-k},(0\le k\le n)\\ C_{n+1}^{k+1}=C_n^k+C_n^{k+1},(1\le k\le n)\end{array}$

- Đặc điểm: Tổ hợp là chọn phần tử không quan trọng thứ tự, số phần tử được chọn là k: $0\le k\le n$

2. Các công thức

Công thức tổ hợp: $C_n^k=\frac{n!}{(n-k)!k!}=\frac{A_n^k}{k!}$

Công thức tính chất của tổ hợp:

$\begin{array}{l}{C}_n^0=C_n^n=1\\ C_n^k=C_n^{n-k},(0\le k\le n)\\ C_{n+1}^{k+1}=C_n^k+C_n^{k+1},(1\le k\le n)\end{array}$

3. Ví dụ minh họa

Ví dụ 1: Một tổ gồm 12 học sinh. Có bao nhiêu cách:

a) Chọn ra 2 bạn đại diện cho nhóm

b) Chọn ra 2 bạn, rồi phân công chứ vụ tổ trưởng và tổ phó

c) Chia tổ thành 2 nhóm, trong đó tổ trưởng và tổ phó khác nhóm

Lời giải

a) Chọn 2 bạn từ 12 bạn là tổ hợp chập 2 của 12: $C_{12}^2=66$ cách.

b) Chọn 2 bạn rồi phân công chức vị là chỉnh hợp chập 2 của 12: $A_{12}^2=132$ cách.

c) Chia tổ thành 2 nhóm tức mỗi nhóm có 6 bạn

Trong đó tổ trưởng và tổ phó khác nhóm

Chọn 5 bạn vào cùng nhóm với tổ trưởng trong 10 bạn còn lại: $C_{10}^5=252$ cách.

Chọn 5 bạn vào cùng nhóm với tổ phó trong 5 bạn còn lại: $C_5^5=1$ cách.

Vậy có 252.1 = 252 cách.

Ví dụ 2: Một hộp có 15 viên bi đỏ và 5 viên bi xanh, 10 viên bi vàng. Có bao nhiêu cách chọn ra 5 viên sao cho

a) Các viên bi cùng màu

b) Số bi xanh bằng số bi đỏ, biết luôn có bi xanh và đỏ

c) Có ít nhất 1 viên bi xanh

Lời giải

a) Chọn 5 viên bi cùng màu

+ Trường hợp 1: Chọn được 5 viên bi màu đỏ: $C_{15}^5=3003$ cách.

+ Trường hợp 2: Chọn được 5 viên bi màu xanh: có $C_5^5=1$ cách.

+ Trường hợp 3: Chọn được 5 viên bi màu xanh: có $C_{10}^5=252$ cách.

Vậy có 3003 + 1 + 252 = 3256 cách chọn.

b) Chọn được 5 viên bi trong đó số bi xanh bằng số bi đỏ

+ Trường hợp 1: có 1 viên bi xanh, 1 viên bi đỏ, 3 viên bi vàng: $C_5^1.C_{15}^1.C_{10}^3=9000$ cách.

+ Trường hợp 2: có 2 viên bi xanh, 2 viên bi đỏ, 1 viên bi vàng: $C_5^2.C_{15}^2.C_{10}^1=10500$ cách.

Vậy có 9000 + 10500 = 19500 cách chọn.

c) Chọn được ít nhất 1 viên bi xanh

Số cách chọn 5 viên bi bất kì là: $C_{30}^5=142506$ cách.

Số cách chọn 5 viên trong đó không có bi xanh là: $C_{25}^5=53130$ cách.

Vậy số cách chọn được ít nhất 1 viên bi xanh là: 142506 – 53130 = 89376 cách chọn.

4. Bài tập vận dụng 

Câu 1: Có 15 tay đua xe đạp cùng xuất phát trong một cuộc đua để chọn ra 3 người về đích đầu tiên. Số kết quả có thể xảy ra là:

A.455    B.910    C.2730    D.2400

Hướng dẫn giải :

Đáp án : A

Cần chọn ra 3 người về đích đầu tiên, nên giữa 3 người này không cần phải phân định thứ tự nhất nhì ba.

Số kết quả xảy ra là: 

Câu 2: Từ một nhóm gồm 6 nam và 5 nữ cần chọn ra 4 người trong đó có ít nhất một nữ. Hỏi có bao nhiêu cách chọn như vậy ?

A.75    B.330    C.315    D.325

Hướng dẫn giải :

Đáp án : C

+ Số cách chọn ra 4 người bất kì từ 11 người là: 

+ Số cách chọn ra 4 nam trong 6 nam là: 

⇒ số cách chọn ra 4 người trong đó có ít nhất 1 nữ là: 330- 15= 315 cách

Câu 3: Trong một trường có 4 học sinh giỏi lớp 12, 3 học sinh giỏi lớp 11 và 5 học sinh giỏi lớp 10. Cần chọn 5 học sinh giỏi để tham gia một cuộc thi với các trường khác sao cho khối 12 có 3 em và mỗi khối 10, 11 có đúng 1 em. Vậy số tất cả các cách chọn là:

A.60    B.180    C.300    D.90

Hướng dẫn giải :

Đáp án : A

Chọn 3 học sinh lớp 12 có 

Chọn 1 học sinh lớp 11 có 

Chọn 1 học sinh lớp 10 có 

Do đó có; 4.3.5= 60 cách chọn

Câu 4: Hai đơn vị thi đấu cờ tướng A và B lần lượt có 5 người và 6 người. Cần chọn ra mỗi đơn vị 3 người để ghép cặp thi đấu với nhau. Hỏi có bao nhiêu cách thực hiện như thế

A.1500    B.1600    C.1200    D.1540

Hướng dẫn giải :

Đáp án : C

+ Số cách chọn 3 người từ đơn vị A là 

+ Số cách chọn 3 người từ đơn vị B là 

+ Sau khi chọn 3 người từ mỗi đơn vị; ta đi ghép các cặp đấu.

Đánh số thứ tự của 3 người từ đơn vị A lần lượt là 1; 2; 3.

Người thứ 1 của đơn vị B có 3 cách chọn; người thứ 2 của đơn vị B có 2 cách chọn và người thứ 3 của đơn vị B có 1 cách chọn.

⇒ Có 3.2.1= 6 cách ghép các cặp đấu.

Vậy có: 10 .20. 6= 1200 cách thực hiện việc ghép cặp thi đấu.

Câu 5: Cho 2 đường thẳng a và b song song với nhau.Trên đường thẳng a lấy 7 điểm phân biệt, trên đường thẳng b lấy 6 điểm phân biệt. Hỏi có thể dựng được bao nhiêu tam giác từ 13 điểm đã cho?

A.240    B.231    C.210    D.180

Hướng dẫn giải :

Đáp án : B

Số tam giác có 1 đỉnh nằm trên a và 2 đỉnh nằm trên b là: 

Số tam giác có 2 đỉnh nằm trên a và 1 đỉnh nằm trên b là: 

Do đó số tam giác có thể dựng được là : 105+ 126 = 231 tam giác

Câu 6: Một hội đồng gồm 5 nam và 4 nữ được tuyển vào một ban quản trị gồm 4 người. Biết rằng ban quản trị có ít nhất một nam và một nữ. Hỏi có bao nhiêu cách tuyển chọn?

A.240    B.180    C.126    D.120

Hướng dẫn giải :

Đáp án : D

Số cách chọn ban quản trị gồm 1 nam và 3 nữ là 

Số cách chọn ban quản trị gồm 2 nam và 2 nữ là 

Số cách chọn ban quản trị gồm 3 nam và 1 nữ là 

Vậy tổng số cách chọn cần tìm là: 20+ 60+ 40= 120 cách.

Câu 7: Bạn Hồng có 15 bông hoa. Trong đó; có 5 bông hoa hồng; 4 bông hoa ly và 6 bông hoa lan. Hỏi bạn Hồng có bao nhiêu cách chọn ra 3 bông hoa hồng; 3 bông hoa ly và 4 bông hoa lan?

A.240    B.300    C.540    D.600

Hướng dẫn giải :

Đáp án : D

+ Số cách chọn ra 3 bông hoa hồng từ 5 bông hoa hồng là: 

+ Số cách chọn ra 3 bông hoa ly từ 4 bông hoa ly là : 

+ Số cách chọn ra 4 bông hoa lan từ 6 bông hoa lan là: 

⇒ Số cách chọn thỏa mãn đầu bài là: 10 .4. 15= 600 cách.

Câu 8: Có 30 câu hỏi khác nhau gồm 5 câu khó, 10 câu trung bình, 15 câu dễ. Từ 30 câu đó có thể lập được bao nhiêu đề kiểm tra, mỗi đề gồm 5 câu khác nhau, sao cho mỗi đề phải có 3loại câu hỏi (khó, trung bình, dễ) và số câu dễ không ít hơn 2?

A.56875    B.58765    C.87625    D.22575

Hướng dẫn giải :

Đáp án : A

Trường hợp 1: Đề gồm 2 câu dễ, 2 câu khó, 1 câu trung bình thì có 

Trường hợp 2: Đề gồm 2 câu dễ, 1 câu khó và 2 câu trung bình thì có 

Trường hợp 3: Đề gồm 3 câu dễ, 1 câu khó và 1 câu trung bình thì có 

Theo quy tắc cộng thì có 10500 + 23625 + 22750 = 56875 đề.

5. Bài tập tự luyện 

Câu 1: Lớp 10 A2 có 20 học sinh nữ và 18 học sinh nam. Hỏi cô giáo chủ nhiệm có bao nhiêu cách chọn ra 3 bạn đi trực nhật.

A.8436    B.7654    C.6548    D.5448

Lời giải:

Đáp án : A

Lớp 10A2 có tất cả 20 + 18= 38 học sinh.

Số cách chọn ra 3 bạn từ 38 bạn là: 

Câu 2: Từ 15 người, Đảng ủy thành lập một ban kiểm tra gồm 1 người lãnh đạo và 3 ủy viên. Hỏi có bao nhiêu cách thành lập ban kiểm tra?

A.1820    B.32760    C.5460    D.10540

Lời giải:

Đáp án : C

Số cách chọn 1 lãnh đạo từ 15 người đã cho: 

Số cách chọn 3 ủy viên từ 14 người còn lại: 

Tổng số cách thành lập ban kiểm tra là: 15. 364= 5460 cách.

Câu 3: Trong một bình đựng 6 viên bi đỏ và 5 viên bi xanh. Lấy ngẫu nhiên ra 2 viên. Có bao nhiêu cách lấy được 2 viên cùng màu?

A.18    B.9    C.22    D.25

Lời giải:

Đáp án : D

Số cách lấy hai viên bi cùng màu đỏ là 

Số cách lấy hai viên bi cùng màu xanh là 

Như vậy số cách lấy đươc hai viên bi cùng màu là: 15 + 10= 25 cách.

Câu 4: Tổ 1 của lớp 11A1 có 10 học sinh; tổ 2 có 11 học sinh; tổ 3 có 11 học sinh và tổ 4 có 10 học sinh. Hỏi giáo viên chủ nhiệm có bao nhiêu cách chọn ra 1 bạn lớp trưởng và 4 bạn tổ trưởng.

A.4253340    B.101270    C.2430480    D.Đáp án khác

Lời giải:

Đáp án : A

+ Lớp 11A1 có tất cả: 10+ 11+ 11+ 10= 42 học sinh.

+ Có 42 cách chọn một bạn làm lớp trưởng.

+ Có 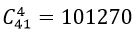 cách chọn 4 bạn làm tổ trưởng trong 41 bạn còn lại...

⇒ Số cách chọn 1 bạn lớp trưởng và 4 bạn làm tổ trưởng là: 42 .101270= 4253340 cách.

Câu 5: Mạnh có 7 người bạn thân trong đó có hai bạn Hùng và Tùng. Mạnh muốn mời 3 trong 7 người bạn đó về quê chơi vào cuối tuần. Số cách mời ba bạn về quê Mạnh chơi sao cho nếu có Hùng thì không có Tùng; nếu có Tùng thì không có Hùng là?

A.20    B.25    C.30    D.40

Lời giải:

Đáp án : C

Trường hợp 1 : Trong 3 bạn được mời, có Hùng nhưng không có Tùng.

Số cách chọn hai bạn còn lại đi cùng Hùng là: 

Trường hợp 2 : có Tùng nhưng không có Hùng

Số cách chọn hai bạn còn lại là: 

Trường hợp 3 : Trong 3 bạn được mời, không có cả Hùng và Tùng

Số cách chọn nhóm 3 người trong trường hợp này là 

Vậy số cách chọn cần tìm là 10 + 10 + 10= 30 cách.

Câu 6: Bạn Mạnh có 10 bông hoa hồng; 8 bông hoa lan và 6 bông hoa huệ. Mạnh muốn chọn ra 6 bông để tặng Hương. Biết rằng số hoa hồng bằng số hoa lan.

A.24681    B.26821    C.18641    D.20241

Lời giải:

Đáp án : B

Trường hợp 1 : Tặng 6 bông hoa huệ: có 1 cách.

Trường hợp 2 : Tặng 1 hoa hồng; 1 hoa lan và 4 hoa huệ: 

Trường hợp 3 : Tặng 2 hoa hồng; 2 hoa lan và 2 hoa huệ có: 

Trường hợp 4 : Tặng 3 hoa hồng; 3 hoa lan có: 

⇒ Số cách tặng thỏa mãn là: 1 + 1200 + 18900 + 6720 = 26821 cách.

Câu 7: Một lớp có 40 học sinh gồm 18 học sinh nam, 22 học sinh nữ, cần chọn ra 5 học sinh gồm cả nam và nữ đi trực tuần. Hỏi có bao nhiêu cách chọn để trong đó có ít nhất 3 nữ?

A.538950    B.905760    C.367290    D.144000

Lời giải:

Đáp án : C

Trường hợp 1: Chọn 3 nữ, 2 nam có 

Trường hợp 2: Chọn 4 nữ, 1 nam có 

Do đó có : 

Câu 8: Công ty A có 6 nam và 5 nữ được xét tuyển vào ban quản trị. Hỏi có bao nhiêu cách lập ra ban quản trị có 5 người; trong đó có ít nhất 2 nam và ít nhất 1 nữ?

A.425    B.375    C.350    D.275

Lời giải:

Đáp án : A

+ Trường hợp 1 : Ban quản trị có 2 nam và 3 nữ: 

+ Trường hợp 2 : Ban quản trị có 3 nam và 2 nữ. 

+ Trường hợp 3 : Ban quản trị có 4 nam và 1 nữ: 

⇒ Số cách lập ra ban quản trị thỏa mãn đầu bài là: 150 + 200 + 75= 425 cách

Câu 9: Có 8 nhà khoa học Toán gồm 6 nam, 2 nữ và 5 nhà khoa học Vật Lí -toàn nam. Hỏi có bao nhiêu cách lập một đội gồm 4 nhà khoa học trong đó có cả nam, nữ, cả Toán, Vật Lí?

A.270    B.185    C.375    D.330

Lời giải:

Đáp án : D

Nếu đã có nữ thì rõ ràng có nhà khoa học Toán, nếu đã có nhà khoa học Vật Lí thì chắc chắn có nam. Do đó ta chỉ cần xét các trường hợp sau:

- Có đúng 1 nữ nhà khoa học Toán, có 2 cách chọn. Lúc này chỉ cần có nhà khoa học Vật Lí là thỏa mãn đề bài, có thể có hoặc không nhà khoa học Toán nam nào khác, số cách chọn 3 nhà khoa học còn lại là 

Vậy số cách lập nhóm trong trường hợp này là: 

- Có đúng 2 nữ nhà khoa học Toán, có 1 cách chọn. Cũng với ý tưởng như trên, chỉ cần có nhà khoa học Vật Lí là thỏa mãn, số cách chọn 2 nhà khoa học còn lại là 

Vậy số cách lập nhóm trong trường hợp này là: 40

⇒ Vậy số cách lập cần tìm là: 290+ 40= 330 cách

Câu 10: Trong một túi đựng 10 viên bi đỏ, 20 viên bi xanh,15 viên bi vàng. Các viên bi có cùng kích cỡ. Số cách lấy ra 5 viên bi và sắp xếp chúng vào 5 ô sao cho 5 ô bi đó có ít nhất một viên bi đỏ.

A.102986240    B.104780240    C.107655240    D.107565240

Lời giải:

Đáp án : C

Bước 1:Chọn ra 5 bi trong đó có ít nhất một viên bi đỏ:

+ Số cách chọn ra 5 viên bi bất kì là 

+ Số cách chọn ra 5 viên bi trong đó không có viên bi đỏ nào là 

+ Số cách chọn ra 5 viên bi trong đó có ít nhất một viên bi màu đỏ là 

Bước 2: Sắp xếp 5 viên bi vừa chọn vào 5 ô:

+ Số cách xếp 5 viên bi vào 5 ô là 5!

+ Theo quy tắc nhân thì có 

Xem thêm các Phương pháp giải bài tập hay, chi tiết khác: 

Công thức khai triển nhị thức Niu-tơn

Công thức tính tổng các hệ số trong khai triển nhị thức Niu-tơn

Công thức tìm hệ số trong khai triển nhị thức Niu-tơn

Công thức tìm số hạng trong khai triển nhị thức Niu-tơn

Công thức tính xác suất