Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Giới hạn của dãy số (HAY NHẤT 2024) gồm đầy đủ các phần: Lý thuyết, phương pháp giải, bài tập minh họa có lời giải chi tiết giúp học sinh làm tốt bài tập Toán 11 từ đó học tốt môn Toán. Mời các bạn đón xem:

Phương pháp giải Giới hạn của dãy số (HAY NHẤT 2024)

1. Lý thuyết

a) Dãy số có giới hạn 0

Ta nói rằng dãy số (u_n) có giới hạn là 0 khi n dần tới dương vô cực, nếu với mỗi số dương nhỏ tùy ý cho trước, mọi số hạng của dãy số kể từ một số hạng nào đó trở đi, |u_n| nhỏ hơn số dương đó.

Kí hiệu: $\underset{n\to \infty }{\lim }{u}_n=0$ hay lim u_n = 0 hay $u_n\to 0$ khi $n\to +\infty$.

b) Dãy số có giới hạn hữu hạn

Ta nói rằng dãy số (u_n) có giới hạn là số thực L nếu lim (u_n – L) = 0

Kí hiệu: $\underset{n\to \infty }{\lim }{u}_n=L$ hay lim u_n = L hay $u_n\to L$ khi $n\to +\infty$.

c) Dãy số có giới hạn vô cực

Dãy số (u_n) có giới hạn là $+\infty$ khi $n\to +\infty$, nếu u_n có thể lớn hơn một số dương bất kì kể từ một số hạng nào đó trở đi.

Ký hiệu: $\lim u_n=+\infty$ hoặc $u_n\to +\infty khin\to +\infty$

Dãy số (u_n) có giới hạn là $-\infty$ khi $n\to +\infty$, nếu $\lim \left(-u_n\right)=+\infty$

Ký hiệu: $\lim u_n=-\infty$ hoặc $u_n\to -\infty khin\to +\infty$

d) Một vài giới hạn đặc biệt

$\lim u_n=0\iff \lim \left|u_n\right|=0$

$\lim \frac{1}{n}=0; \lim \frac{1}{n^k}=0,\left(k>0,k\in {\mathbb{N}}^{*}\right)$

$\lim n^k=+\infty ,\left(k>0,k\in {\mathbb{N}}^{*}\right)$

$\lim q^n=\left\{\begin{array}{l}0 khi\left|q\right|<1\\ +\infty khiq>1\end{array}\right.$

e) Định lý về giới hạn hữu hạn

* Nếu lim u_n = a và lim v_n = b và c là hằng số. Khi đó ta có :

lim(u_n + v_n) = a + b

lim(u_n - v_n) = a - b

lim(u_n v_n) = a.b

$\lim \frac{u_n}{v_n}=\frac{a}{b},\left(b\ne 0\right)$

lim(cu_n ) = c.a

lim|u_n | = |a|

$\lim \sqrt[3]{u_n}=\sqrt[3]{a}$

Nếu $u_n\ge 0$ với mọi n thì $a\ge 0$ và $\lim \sqrt{u_n}=\sqrt{a}$.

* Định lí kẹp: Cho ba dãy số (v_n); (u_n) và (w_n):

Nếu $\left\{\begin{array}{l}\left(v_n\right)\le \left(u_n\right)\le \left({\text{w}}_n\right),\forall n\in N^{*}\\ \lim v_n=\lim w_n=a\end{array}\right.$ thì lim u_n = a.

Hệ quả: Cho hai dãy số (u_n) và (v_n):

Nếu $\left\{\begin{array}{l}\left|u_n\right|\le v_n,\forall n\in N^{*}\\ \lim v_n=0\end{array}\right.$ thì lim u_n = 0.

f) Một vài quy tắc tìm giới hạn vô cực

* Quy tắc tìm giới hạn tích lim (u_nv_n)

Nếu $\lim u_n=L\ne 0,\lim v_n=+\infty (hay-\infty )$. Khi đó: lim (u_nv_n)

* Quy tắc tìm giới hạn thương

g) Tổng cấp số nhân lùi vô hạn

Xét cấp số nhân vô hạn u₁; u₁q; u₁q²; … u₁qⁿ; … có công bội |q| < 1 được gọi là cấp số nhân lùi vô hạn.

Tổng của cấp số nhân lùi vô hạn là: $S=u_1+u_{1}q+u_1{q}^2+\mathrm{....}=\frac{u_1}{1-q}\left(\left|q\right|<1\right)$

2. Các dạng toán

Dạng 1: Tính giới hạn sử dụng một vài giới hạn đặc biệt

Phương pháp giải:

Sử dụng các giới hạn đặc biệt:

$\lim u_n=0\iff \lim \left|u_n\right|=0$

$$\begin{gathered} \lim \frac{1}{n}=0;\lim \frac{1}{n^k}=0,\left(k>0,k\in {\mathbb{N}}^{*}\right) \\ \lim n^k=+\infty ,\left(k>0,k\in {\mathbb{N}}^{*}\right) \end{gathered}$$

$\lim q^n=\left\{\begin{array}{l}0khi\left|q\right|<1\\ +\infty khiq>1\end{array}\right.$

Ví dụ minh họa:

Ví dụ 1: Tính các giới hạn sau:

a) $\lim \frac{1}{n^2}$

b) $\lim \frac{1}{n^2+n+3}$

c) $\lim \frac{1}{n\sqrt{n}}$

Lời giải

Áp dụng công thức tính giới hạn đặc biệt, ta có:

a) $\lim \frac{1}{n^2}=0$

b) $\lim \frac{1}{n^2+n+3}=0$

c) $\lim \frac{1}{n\sqrt{n}}=0$

Ví dụ 2: Tính các giới hạn sau:

a) $\lim {\left(\frac{1}{2}\right)}^n$

b) $\lim {\left(\frac{5}{4}\right)}^{n+1}$

c) lim (-0,999)ⁿ

Lời giải

a) $\lim {\left(\frac{1}{2}\right)}^n=0$ vì $\left|\frac{1}{2}\right|<1$

b) $\lim {\left(\frac{5}{4}\right)}^{n+1}=+\infty$ vì $\frac{5}{4}>1$

c) lim (-0,999)ⁿ = 0 vì |-0,999| < 1.

Dạng 2: Tính giới hạn hữu hạn của phân thức

Phương pháp giải:

Trường hợp lũy thừa của n: Chia cả tử và và mẫu cho n^k (với n^k là lũy thừa với số mũ lớn nhất).

Trường hợp lũy thừa mũ n: Chia cả tử và mẫu cho lũy thừa có cơ số lớn nhất.

Sử dụng một vài giới hạn đặc biệt:

$\begin{array}{l}\lim u_n=0\iff \lim \left|u_n\right|=0\\ \lim \frac{1}{n}=0;\lim \frac{1}{n^k}=0,\left(k>0,k\in {\mathbb{N}}^{*}\right)\\ \lim n^k=+\infty ,\left(k>0,k\in {\mathbb{N}}^{*}\right)\\ \lim q^n=\left\{\begin{array}{l}0 khi\left|q\right|<1\\ +\infty khiq>1\end{array}\right.\end{array}$

Ví dụ minh họa:

Ví dụ 1: Tính các giới hạn sau

a) $\lim \frac{-2n^3+3n^2+4}{n^4+4n^3+n}$

b) $\lim \frac{{\left(-5\right)}^n+4^n}{{\left(-7\right)}^{n+1}+4^{n+1}}$

c) $\lim \frac{2n\sqrt{n}+1}{n^2+2\sqrt{n}-3}$

Lời giải

a) $\lim \frac{-2n^3+3n^2+4}{n^4+4n^3+n}=\lim \frac{\frac{-2n^3+3n^2+4}{n^4}}{\frac{n^4+4n^3+n}{n^4}}$

$=\lim \frac{-\frac{2}{n}+\frac{3}{n^2}+\frac{4}{n^4}}{1+\frac{4}{n}+\frac{1}{n^3}}=\frac{-0+0+4}{1+0+0}=0$

Vì $\lim \frac{2}{n}=0, \lim \frac{3}{n^2}=0,$$\lim \frac{4}{n^4}=0, \lim \frac{4}{n}=0$ và $\lim \frac{1}{n^3}=0$.

b) $\lim \frac{{\left(-5\right)}^n+4^n}{{\left(-7\right)}^{n+1}+4^{n+1}}=\lim \frac{\frac{{\left(-5\right)}^n}{{\left(-7\right)}^{n+1}}+\frac{4^n}{{\left(-7\right)}^{n+1}}}{\frac{{\left(-7\right)}^{n+1}}{{\left(-7\right)}^{n+1}}+\frac{4^{n+1}}{{\left(-7\right)}^{n+1}}}$

$=\lim \frac{\frac{1}{-7}.{\left(\frac{-5}{-7}\right)}^n+\frac{1}{-7}.{\left(\frac{4}{-7}\right)}^n}{1+{\left(\frac{4}{-7}\right)}^{n+1}}=\frac{\frac{1}{-7}.0+\frac{1}{-7}.0}{1+0}=0$

Vì  $\lim {\left(\frac{-5}{-7}\right)}^n=\lim {\left(\frac{4}{-7}\right)}^n=0$

c) $\lim \frac{2n\sqrt{n}+1}{n^2+2\sqrt{n}-3}=\lim \frac{\frac{2n\sqrt{n}+1}{n^2}}{\frac{n^2+2\sqrt{n}-3}{n^2}}$

$=\lim \frac{\frac{2}{\sqrt{n}}+\frac{1}{n^2}}{1+\frac{2}{n\sqrt{n}}-\frac{3}{n^2}}=\frac{0+0}{1+0-0}=0$

Vì $\lim \frac{2}{\sqrt{n}}=0,\lim \frac{1}{n^2}=0,$$\lim \frac{2}{n\sqrt{n}}=0,\lim \frac{3}{n^2}=0$

Ví dụ 2: Tính các giới hạn sau:

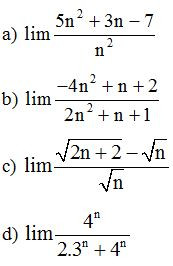
Lời giải

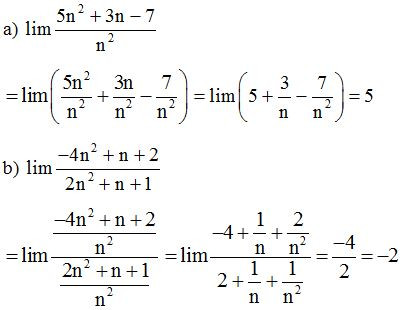
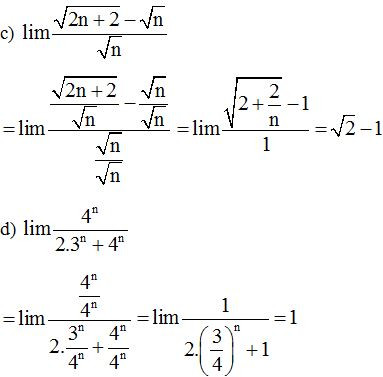
Dạng 3: Tính giới hạn hữu hạn sử dụng phương pháp liên hợp

Phương pháp giải: Sử dụng các công thức liên hợp (thường sử dụng trong các bài toán chứa căn)

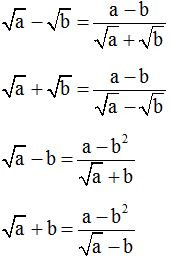
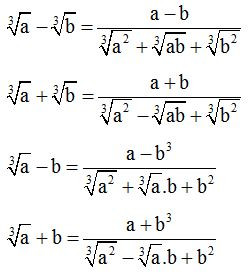
Ví dụ minh họa:

Ví dụ 1: Tính các giới hạn sau:

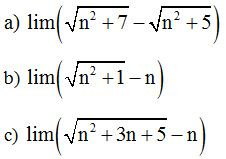
Lời giải

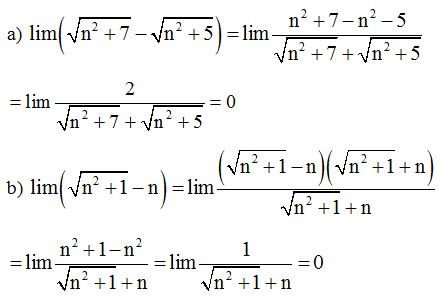
Ví dụ 2: Tính giới hạn sau: $\lim \left(\sqrt[3]{n^3+3n^2}-n\right)$

Lời giải

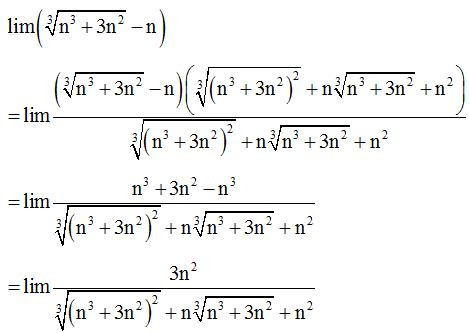
Dạng 4: Tính giới hạn ra vô cực dạng chứa đa thức hoặc căn thức

Phương pháp giải:

Rút bậc lớn nhất của đa thức làm nhân tử chung.

Sử dụng quy tắc giới hạn tới vô cực lim (u_nv_n)

Nếu $\lim u_n=L\ne 0,\lim v_n=+\infty (hay-\infty )$. Khi đó: lim (u_nv_n)

Ví dụ minh họa:

Ví dụ 1: Tính các giới hạn sau:

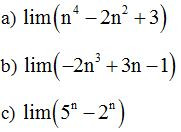
Lời giải

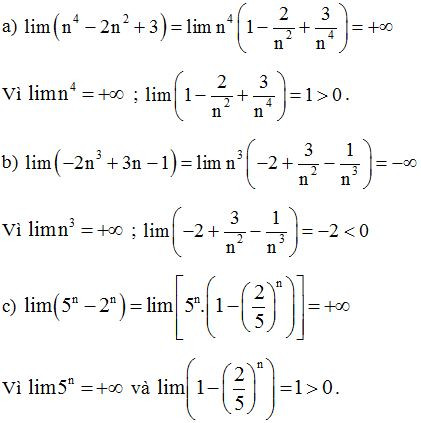
Ví dụ 2: Tính các giới hạn sau

a) $\lim \left(2n-\sqrt{n^3+2n-2}\right)$

b) $\lim \left(n^2-n\sqrt{4n+1}\right)$

Lời giải

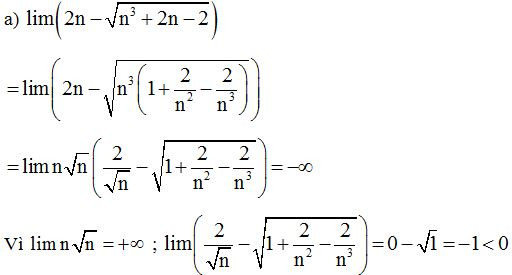
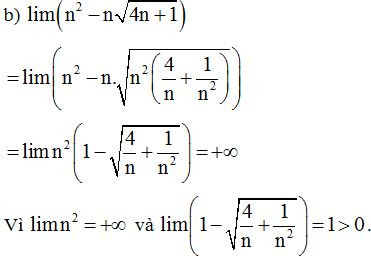
Dạng 5: Tính giới hạn ra vô cực dạng phân thức

Phương pháp giải:

Rút bậc lớn nhất của tử và mẫu ra làm nhân tử chung.

Sử dụng quy tắc giới hạn tới vô cực lim (u_nv_n)

Nếu $\lim u_n=L\ne 0,\lim v_n=+\infty (hay-\infty )$. Khi đó: lim (u_nv_n)

Ví dụ minh họa:

Ví dụ 1: Tính các giới hạn sau:

a) $\lim \frac{2n^4-3n^3+2}{n^3+2}$

b) $\lim \frac{\left(2n-1\right){\left(3n^2+2\right)}^3}{-2n^5+4n^3-1}$

Lời giải

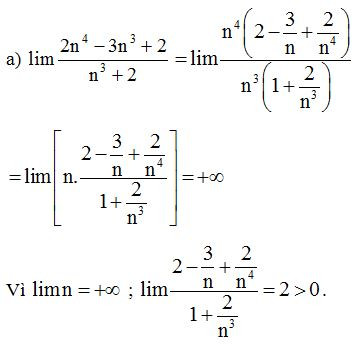
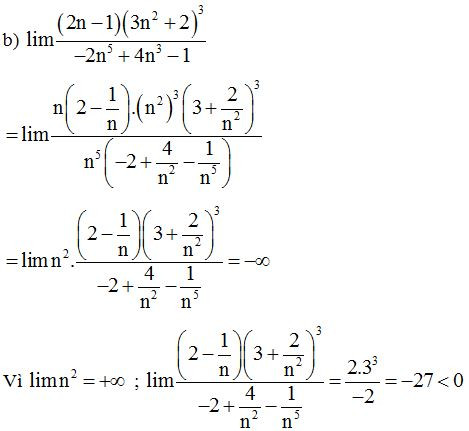
Ví dụ 2: Tính giới hạn sau $\lim \frac{3n^2-\sqrt{2n^4+3n-2}}{4n-\sqrt{3n^2+2}}$.

Lời giải

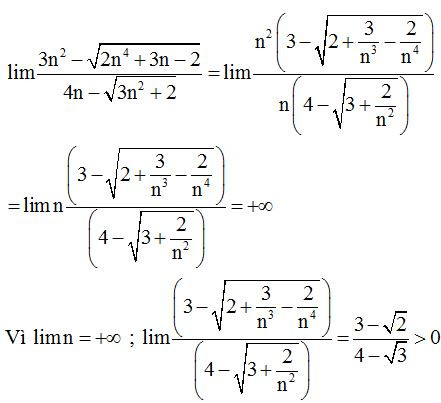
Dạng 6: Tính giới hạn sử dụng định lý kẹp

Phương pháp giải:

Sử dụng định lý kẹp và hệ quả của định lý kẹp

Định lí kẹp: Cho ba dãy số (v_n); (u_n) và (w_n): Nếu $\left\{\begin{array}{l}\left(v_n\right)\le \left(u_n\right)\le \left({\text{w}}_n\right),\forall n\in N^{*}\\ \lim v_n=\lim w_n=a\end{array}\right.$ thì lim u_n = a

Hệ quả: Cho hai dãy số (u_n) và (v_n): Nếu $\left\{\begin{array}{l}\left|u_n\right|\le v_n,\forall n\in N^{*}\\ \lim v_n=0\end{array}\right.$ thì lim u_n = 0.

Ví dụ minh họa:

Ví dụ 1: Tính các giới hạn sau:

a) $\lim \frac{{\left(-1\right)}^n}{n+4}$

b) $\lim \left(\frac{{\left(-1\right)}^n}{2^{n+1}}-\frac{1}{3^{n+1}}\right)$

Lời giải

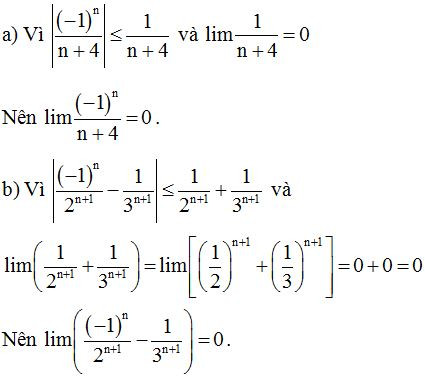
Ví dụ 2: Tính các giới hạn sau :

a) $\lim \frac{{\sin }^{2}n}{n+2}$

b) $\lim \frac{1+\cos n^3}{2n+3}$

Lời giải

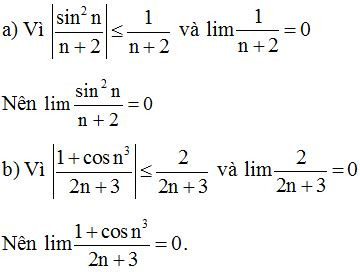
Dạng 7: Giới hạn dãy số có công thức truy hồi

Phương pháp giải:

Cho dãy số (u_n) ở dạng công thức truy hồi, biết (u_n) có giới hạn hữu hạn

Giả sử lim u_n = a (a là số thực) thì lim u_n+1 = a.

Thay a vào công thức truy hồi. Giải phương trình tìm a.

Ta được giới hạn của (u_n) là lim u_n = a.

Ví dụ minh họa:

Ví dụ 1: Tìm lim u_n biết (u_n) có giới hạn hữu hạn và $\left(u_n\right):\left\{\begin{array}{l}{u}_1=1\\ u_{n+1}=\frac{2u_n+3}{u_n+2},n\in {\mathbb{N}}^{*}\end{array}\right.$

Lời giải

Giả sử lim u_n = a, khi đó lim u_n+1 = a

Suy ra $a=\frac{2\text{a}+3}{a+2}\Rightarrow a^2+2a=2a+3$$\iff a^2=3\iff a=\pm \sqrt{3}$

Do $u_1=1>0,u_{n+1}=\frac{2u_n+3}{u_n+2}>0\forall n\in {\mathbb{N}}^{*}$ nên $a>0\Rightarrow a=\sqrt{3}$

Vậy $\lim u_n=\sqrt{3}$.

Ví dụ 2: Tìm lim u_n biết (u_n) có giới hạn hữu hạn và $\left(u_n\right):\left\{\begin{array}{l}{u}_1=\sqrt{2}\\ u_{n+1}=\sqrt{2+u_n},n\in {\mathbb{N}}^{*}\end{array}\right.$.

Lời giải

Vì $u_1=\sqrt{2}>0;u_{n+1}=\sqrt{2+u_n}>0$

Giả sử lim u_n = a (a > 0), khi đó lim u_n+1 = a

Suy ra $a=\sqrt{2+a}\iff a^2=a+2$

$$\begin{gathered} \iff a^2-a-2=0 \\ \iff \left[\begin{array}{l}a=-1\left(Loại\right)\\ a=2\end{array}\right. \end{gathered}$$

Vậy lim u_n = 2.

Dạng 8: Giới hạn của tổng vô hạn hoặc tích vô hạn

Phương pháp giải:

* Rút gọn (u_n) (sử dụng tổng cấp số cộng, cấp số nhân hoặc phương pháp làm trội)

* Rồi tìm lim u_n theo định lí hoặc dùng nguyên lí định lí kẹp.

* Định lí kẹp: Cho ba dãy số (v_n); (u_n) và (w_n): Nếu $\left\{\begin{array}{l}\left(v_n\right)\le \left(u_n\right)\le \left({\text{w}}_n\right),\forall n\in N^{*}\\ \lim v_n=\lim w_n=a\end{array}\right.$ thì lim u_n = a

Hệ quả: Cho hai dãy số (u_n) và (v_n): Nếu $\left\{\begin{array}{l}\left|u_n\right|\le v_n,\forall n\in N^{*}\\ \lim v_n=0\end{array}\right.$ thì lim u_n = 0.

Ví dụ minh họa:

Ví dụ 1: Tính các giới hạn sau:

a) $\lim \left(\frac{1}{1.3}+\frac{1}{3.5}+\mathrm{...}+\frac{1}{\left(2n-1\right)\left(2n+1\right)}\right)$

b) $\lim \frac{1+2+3+4+\mathrm{...}+n}{\left(1+3+3^2+3^3+\mathrm{...}+3^n\right).\left(n+1\right)}$

Lời giải

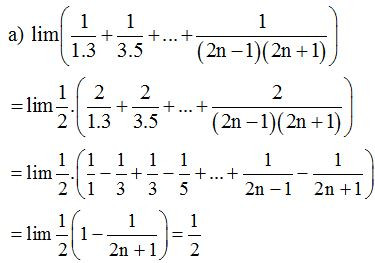
b) $L=\lim \frac{1+2+3+4+\mathrm{...}+n}{\left(1+3+3^2+3^3+\mathrm{...}+3^n\right).\left(n+1\right)}$

Xét tử số: Ta thấy 1; 2; 3; 4; … ; n là một dãy số thuộc cấp số cộng có n số hạng với u₁ = 1 và d = 1.

Tổng n số hạng của cấp số cộng: $S_n=\frac{\left(u_1+u_n\right)n}{2}=\frac{\left(1+n\right)n}{2}.$

Xét mẫu số: Ta thấy 1; 3 ; 3² ; 3³ ; … ; 3ⁿ là một dãy số thuộc cấp số nhân có (n+1) số hạng với u₁ = 1 và q = 3.

Tổng (n + 1) số hạng của cấp số nhân: $S_{n+1}=u_1.\frac{1-q^{n+1}}{1-q}=\frac{1-3^{n+1}}{1-3}=\frac{3^{n+1}-1}{2}.$

 Khi đó: $L=\lim \frac{\frac{\left(1+n\right)n}{2}}{\frac{3^{n+1}-1}{2}.(n+1)}=\lim \frac{n}{3^{n+1}-1}$

Vì $\left|\frac{n}{3^{n+1}-1}\right|=\left|\frac{n}{{3.3}^n-1}\right|<\frac{n}{3^n}<\frac{2^n}{3^n}={\left(\frac{2}{3}\right)}^n$ và $\lim {\left(\frac{2}{3}\right)}^n=0$

Nên $L=\lim \frac{n}{3^{n+1}-1}=0$

(Bằng quy nạp ta luôn có $n<2^n,\forall n\in {\mathbb{N}}^{*}$ và $3^n>1,\forall n\in {\mathbb{N}}^{*}$$\Rightarrow 3^{n+1}-3^n={2.3}^n>2>1$$\Rightarrow 3^{n+1}-1>3^n$).

4. Bài tập vận dụng 

Bài 1: Tính 

Hướng dẫn:

Ta có

Mà

Vậy 

Bài 2: Tính 

Hướng dẫn:

Khi đó 

Bài 3: Tính 

Hướng dẫn:

Bài 4: Tính 

Hướng dẫn:

Bài 5: Cho dãy số (u_n). Biết 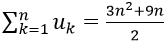 với mọi n ≥ 1. Tìm 

Hướng dẫn:

Bài 6: Cho dãy số (u_n) với 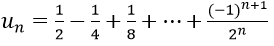. Tính lim u_n

Hướng dẫn:

u_n là tổng n số hạng đầu tiên của một cấp số nhân có u₁ = 1/2 và q = (-1)/2.

Do đó

Bài 7: Tính lim 

Hướng dẫn:

Vậy 

5. Bài tập tự luyện 

Bài 1: Tính giới hạn: 

A. 0             B. 1            C. 3/2              D. Không có giới hạn

Bài 2: Tính giới hạn: 

A. 1            B. 0            C. 2/3            D. 2

Bài 3: 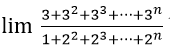 bằng:

+∞            B. 3            C. 3/2            D. 2/3

Bài 4: Tính giới hạn: 

A. 1            B. 1/2            C. 1/4            D. 3/2

Bài 5: Cho dãy số (u_n) với 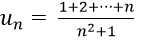. Mệnh đề nào sau đây là mệnh đề đúng?

A. lim⁡u_n = 0

B. lim⁡u_n = 1/2

C. lim⁡u_n = 1

D. Dãy số (u_n) không có giới hạn khi n → +∞

Bài 6: Tìm giá trị đúng của 

A. √2 + 1.             B. 2.             C. 2√2.             D. 1/2.

Bài 7: Tính giới hạn: 

A. 0            B. 1/3            C. 2/3            D. 1

Bài 8: 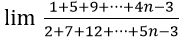 bằng:

Bài 9: Tính giới hạn: 

A. 1/2            B. 1            C. 0            D. 2/3

Bài 10: Tính giới hạn: 

A. 11/18            B. 2            C. 1            D. 3/2

Xem các phương pháp giải bài tập hay, chi tiết khác:

Giới hạn của hàm số và cách giải bài tập

Hàm số liên tục và cách giải bài tập

Cách tính đạo hàm bằng định nghĩa hay, chi tiết

Quy tắc tính đạo hàm và cách giải bài tập

Đạo hàm của hàm số lượng giác và cách giải