Giải Vở thực hành Toán 8 (Kết nối tri thức) Bài Luyện tập chung trang 49

Nguyễn Lê Khánh Vy Ngày: 16-08-2023 Lớp 8

384

Toptailieu.vn biên soạn và giới thiệu giải Giải Vở thực hành Toán 8 (Kết nối tri thức) Bài Luyện tập chung trang 49 hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm các bài tập từ đó nâng cao kiến thức và biết cách vận dụng phương pháp giải vào các bài tập Toán 8. Mời các bạn cùng đón xem:

Giải Vở thực hành Toán 8 (Kết nối tri thức) Bài Luyện tập chung trang 49

Bài 1 trang 49 vở thực hành Toán 8 Tập 1: Tứ giác ABCD trong Hình 3.14 có phải là hình thang không? Vì sao?

(ảnh 1)

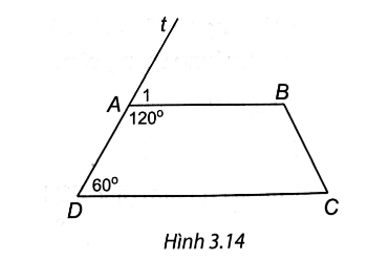
Lời giải:

Gọi At là tia đối của tia AD thì $\hat{t A B} = 180 ° - 120 ° = 60 ° .$

Do đó $\hat{t A B} = \hat{A D C},$ suy ra AB // DC (hai góc đồng vị bằng nhau).

Vậy ABCD là hình thang với hai cạnh đáy là AB và CD.

Bài 2 trang 50 vở thực hành Toán 8 Tập 1: Cho hình thang cân ABCD (AB // CD) có AB = AD. Biết $\hat{A B D} = 30 °,$ tính số đo góc của hình thang đó.

Lời giải:

(ảnh 2)

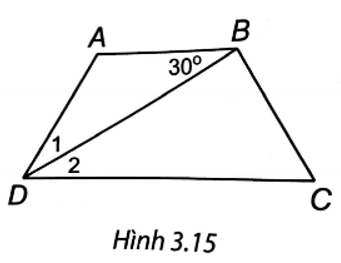
(H.3.15). Tam giác ABD có AB = AD nên ∆ABD cân tại A, do đó ${\hat{D}}_{1} = \hat{A B D} = 30 ° .$

Vì AB // CD nên ${\hat{D}}_{2} = \hat{A B D} = 30 ° .$ (hai góc so le trong); suy ra $\hat{A D C} = {\hat{D}}_{1} + {\hat{D}}_{2} = 60 ° .$

Vì ABCD là hình thang cân nên $\hat{C} = \hat{A D C} = 60 °, \hat{A} = 180 ° - \hat{A D C} = 120 ° = \hat{A B C} .$

Bài 3 trang 50 vở thực hành Toán 8 Tập 1: Tính số đo các góc của tứ giác ABCD trong Hình 3.16.

(ảnh 3)

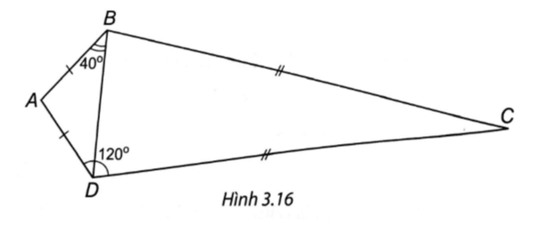
Lời giải:

Tam giác ABD cân tại A nên $\hat{A} = 180 ° - 2 \hat{A B D} = 100 ° .$

Ta có $\hat{A D C} = 120 °; \hat{A D B} = 40 °$ nên $\hat{B D C} = 80 ° .$

Tam giác CBD cân tại C nên $\hat{C} = 180 ° - 2 \hat{B D C} = 20 ° .$

Tứ giác ABCD có $\hat{B} = 360 ° - 120 ° - 20 ° - 100 ° = 120 ° .$

Chú ý. Có thể thấy $\hat{B} = \hat{A B D} + \hat{D B C} = 40 ° + 80 ° .$

Bài 4 trang 50 vở thực hành Toán 8 Tập 1: Cho M là một điểm nằm trong tam giác đều ABC. Qua M kẻ các đường thẳng song song với BC, CA, AB lần lượt cắt AB, BC, CA tại các điểm P, Q, R.

a) Chứng minh tứ giác APMR là hình thang cân.

b) Chứng minh rằng chu vi tam giác PQR bằng tổng độ dài MA + MB + MC.

c) Hỏi với vị trí nào của M thì tam giác PQR là tam giác đều.

Lời giải:

(ảnh 4)

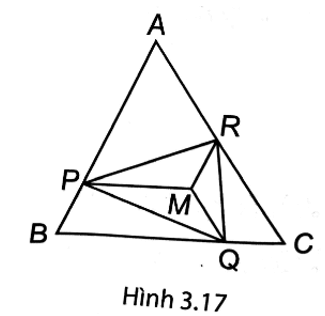
(H.3.17). a) Do MR // AP nên tứ giác APMR là hình thang.

Ta có $\hat{A} = 60 °$ (do ∆ABC đều).

Do MP // BC nên $\hat{B} = \hat{A P M} = 60 ° .$ Từ đó suy ra $\hat{A} = \hat{A P M}$ nên APMR là hình thang cân.

b) Tương tự câu a, ta có các tứ giác BQMP và CRMQ là những hình thang cân.

Do APMR, BQMP và CRMQ là những hình thang cân, suy ra RP = AM, PQ = BM, QR = CM (hai đường chéo của hình thang cân).

Chu vi của tam giác PQR là

PQ + RP + QR = BM + AM + CM.

c) Tam giác PQR là tam giác đều có nghĩa là PQ = QR = RP, tức là MB = MC = MA.

Vậy M cách đều ba đỉnh A, B, C tức M là giao điểm của ba đường trung trực của tam giác ABC.

Bài 5 trang 51 vở thực hành Toán 8 Tập 1: Cho tam giác ABC cân tại A. Trên cạnh AB lấy điểm M, trên cạnh AC lấy điểm N sao cho AM = AN.

a) Tính số đo góc AMN theo góc A.

b) Tứ giác BMNC là hình gì? Vì sao?

c) Cho BM = MN = NC, chứng minh BN là phân giác của góc ABC, CM là phân giác của góc ACB.

Lời giải:

(ảnh 5)

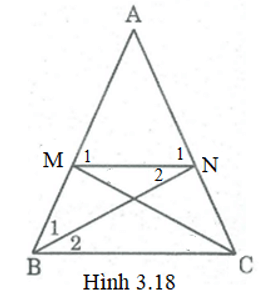
(H.3.18). a) Ta có AM = AN (giả thiết) nên ∆AMN cân tại A

$\Rightarrow {\hat{M}}_{1} = {\hat{N}}_{1} = \frac{180 ° - \hat{A}}{2} .$

b) Vì ∆ABC cân tại A nên $\hat{B} = \hat{C} = \frac{180 ° - \hat{A}}{2} .$

Suy ra ${\hat{M}}_{1} = \hat{B} \Rightarrow$ MN // BC (do có cặp góc đồng vị bằng nhau), từ đó tứ giác BMNC là hình thang.

Mặt khác $\hat{B} = \hat{C}$ nên BMNC là hình thang cân.

c) Ta có BM = MN ⇒ ∆BMN cân tại M $\Rightarrow {\hat{B}}_{1} = {\hat{N}}_{2} .$

Do MN // BC nên ${\hat{B}}_{2} = {\hat{N}}_{2}$ (hai góc so le trong). Từ đó suy ra ${\hat{B}}_{1} = {\hat{B}}_{2},$ tức BN là tia phân giác của góc ABC.