Toptailieu.vn biên soạn và giới thiệu giải Giải Vở thực hành Toán 8 (Kết nối tri thức) Bài 12: Hình bình hành hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm các bài tập từ đó nâng cao kiến thức và biết cách vận dụng phương pháp giải vào các bài tập Toán 8. Mời các bạn cùng đón xem:

Giải Vở thực hành Toán 8 (Kết nối tri thức) Bài 12: Hình bình hành

Câu 1 trang 52 vở thực hành Toán 8 Tập 1: Hãy chọn câu sai.

A. Hình bình hành có hai đường chéo cắt nhau tại trung điểm mỗi đường.

B. Hình bình hành có hai góc đối bằng nhau.

C. Hình bình hành có các cạnh đối song song và bằng nhau.

D. Hình bình hành có hai đường chéo vuông góc với nhau.

Lời giải:

Đáp án đúng là: D

Theo tính chất của hình bình hành thì có các cạnh đối bằng nhau, các góc đối bằng nhau, hai đường chéo cắt nhau tại trung điểm mỗi đường.

Do đó câu sai là: Hình bình hành có hai đường chéo vuông góc với nhau.

Câu 2 trang 52 vở thực hành Toán 8 Tập 1: Điền cụm từ thích hợp vào chỗ trống.

a) Tứ giác có các ............. đối ............................................ là một hình bình hành.

b) Tứ giác có ............................................. song song và .................................................. là một hình bình hành.

c) Trong hình bình hành, hai góc kề ................. bất kì có ...................... bằng $180°.$

d) Tứ giác có ............................................... cắt nhau tại ........................................ của mỗi đường là hình bình hành.

e) Tứ giác có các góc ........................................... là một hình bình hành.

Lời giải:

a) Tứ giác có các cạnh đối bằng nhau là một hình bình hành.

b) Tứ giác có các cạnh đối song song và bằng nhau là một hình bình hành.

c) Trong hình bình hành, hai góc kề một cạnh bất kì có tổng số đo góc bằng $180°.$

d) Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.

e) Tứ giác có các góc đối bằng nhau là một hình bình hành.

Câu 3 trang 52 vở thực hành Toán 8 Tập 1: Cho hình bình hành ABCD có $\widehat{A}=120°.$ Khi đó:

A. $\widehat{B}=120°,\widehat{C}=60°,\widehat{D}=120°.$

B. AB // DC, AB = BC.

C. $\widehat{B}=60°,\widehat{C}=120°,\widehat{D}=60°.$

D. $\widehat{B}=\widehat{D}=60°,\widehat{C}=60°.$

Lời giải:

Đáp án đúng là: C

Hình bình hành ABCD có AB // DC, AB = CD nên B sai.

Ta có $\widehat{A}=120°$ mà AB // DC, suy ra $\widehat{D}=180°-\widehat{A}=60°.$

Mà hình bình hành có hai góc đối bằng nhau nên $\widehat{D}=\widehat{B}=60°;\widehat{A}=\widehat{C}=120°.$

Vậy C là đáp án đúng.

C – BÀI TẬP

Bài 1 trang 52, 53 vở thực hành Toán 8 Tập 1: Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai? Vì sao?

a) Hình thang có hai cạnh bên song song là hình bình hành.

b) Hình thang có hai cạnh bên bằng nhau là hình bình hành.

c) Tứ giác có hai cạnh đối nào cũng song song là hình bình hành.

Lời giải:

a) Đúng, vì tứ giác có các cạnh đối song song là hình bình hành (theo định nghĩa).

b) Sai, vì hình thang cân có hai cạnh bên bằng nhau mà không song song thì không phải là hình bình hành.

c) Đúng, vì tứ giác có các cặp cạnh đối song song và bằng nhau là hình bình hành (theo định nghĩa).

Bài 2 trang 53 vở thực hành Toán 8 Tập 1: Tính các góc còn lại của hình bình hành ABCD trong Hình 3.19.

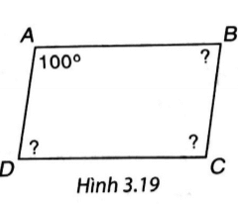
Lời giải:

Hình bình hành có các góc đối bằng nhau và các góc kề bù nhau nên

$\widehat{C}=100°,\widehat{B}=180°-\widehat{A}=80°,\widehat{D}=80°.$

Bài 3 trang 53 vở thực hành Toán 8 Tập 1: Trong mỗi trường hợp sau đây, tứ giác nào là hình bình hành, tứ giác nào không là hình bình hành? Vì sao?

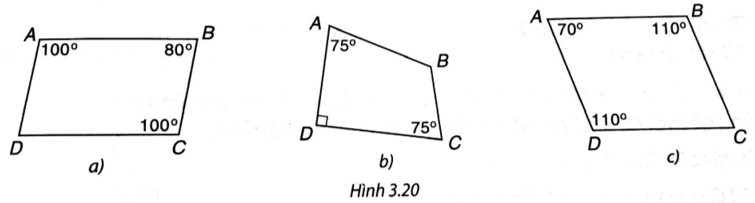
Lời giải:

a) Tứ giác ABCD là hình bình hành vì $\widehat{B}=\widehat{D}=80°$ và $\widehat{A}=\widehat{C}=100°$

b) Tứ giác ABCD không là hình bình hành vì nếu nó là hình bình hành thì hai góc đối bằng nhau và khi đó tổng số đo bốn góc của tứ giác ABCD bé hơn $360°.$

c) Do tổng số đo bốn góc của tứ giác ABCD bằng $360°.$ nên $\widehat{D}=70°.$ Khi đó, ABCD là hình bình hành vì các góc đối của nó bằng nhau.

Vậy ABCD là hình bình hành.

Bài 4 trang 53 vở thực hành Toán 8 Tập 1: Cho hình bình hành ABCD. Gọi E, F lần lượt là trung điểm của các cạnh AB, CD. Chứng minh rằng:

a) Hai tứ giác AEFD, AECF là những hình bình hành.

b) EF = AD, AF = EC.

Lời giải:

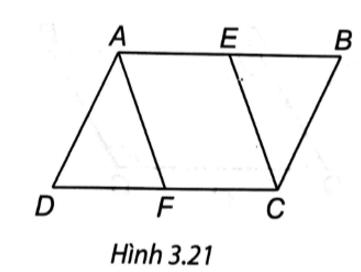
(H.3.21). a) Do ABCD là hình bình hành nên AB // CD, AB = CD, từ đó AE // CF, AE = EB = DF = FC.

Do đó tứ giác AEFD là hình bình hành.

Tương tự, tứ giác AECF là hình bình hành vì có hai cạnh đối AE và CF song song và bằng nhau.

b) Vì AEFD là hình bình hành nên AD = EF.

Vì AECF là hình bình hành nên AF = EC.

Bài 5 trang 54 vở thực hành Toán 8 Tập 1: Gọi O là giao điểm của hai đường chéo của hình bình hành ABCD. Một đường thẳng đi qua O lần lượt cắt các cạnh AB, CD của hình bình hành tại hai điểm M, N. Chứng minh ∆OAM = ∆OCN. Từ đó suy ra tứ giác MBND là hình bình hành.

Lời giải:

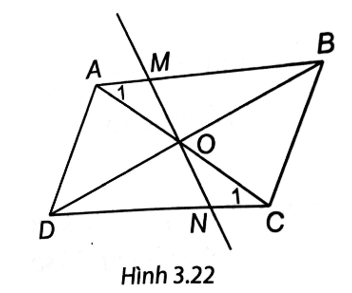
(H.3.22). ABCD là hình bình hành nên AO = CO, BO = DO.

Xét ∆OAM và ∆OCN có: $\widehat{OAM}=\widehat{OCN}$ (hai góc so le trong), $\widehat{AOM}=\widehat{CON}$ (hai góc đối đỉnh), AO = CO nên ∆OAM = ∆OCN (g.c.g).

Suy ra OM = ON.

Ta có OM = ON, BO = DO nên tứ giác MBND có hai đường chéo MN, BD cắt nhau tại trung điểm mỗi đường nên MBND là hình bình hành.

Bài 6 trang 54 vở thực hành Toán 8 Tập 1: Cho tam giác nhọn ABC có trực tâm H. Vẽ các đường thẳng d vuông góc với AB tại B, d’ vuông góc với AC tại C, d và d’ cắt nhau tại N. Chứng mình rằng:

a) Tứ giác BHCN là hình bình hành.

b) HN đi qua trung điểm I của đoạn thẳng BC.

Lời giải:

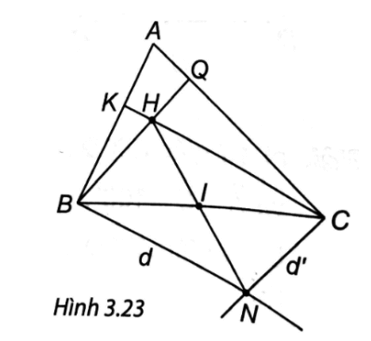
(H.3.23). Vì H là trực tâm của ∆ABC nên CH ⊥ AB, BH ⊥ AC.

Ta có CH ⊥ AB, NB ⊥ AB ⇒ CH // NB.

Tương tự BH // CN.

Từ đó, suy ra BHCN là hình bình hành.

b) Ta có BHCN là hình bình hành nên BC và HN cắt nhau tại trung điểm mỗi đường, do đó HN đi qua trung điểm I của đoạn thẳng BC.

Xem thêm Lời giải bài tập Vở thực hành Toán 8 Kết nối tri thức hay, chi tiết khác: 

Luyện tập chung trang 49

Luyện tập chung trang 54

Bài 13: Hình chữ nhật

Bài 14: Hình thoi và hình vuông

Luyện tập chung trang 63