Với Giải Câu 5 trang 64 VTH Toán 8 Tập 1 lớp 8 trong Bài Luyện tập chung trang 63 Vở thực hành Toán 8 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong Vở thực hành Toán 8.
Cho hình vuông ABCD. Trên cạnh BC lấy điểm N
Bài 5 trang 64 vở thực hành Toán 8 Tập 1: Cho hình vuông ABCD. Trên cạnh BC lấy điểm N. Từ A kẻ đường thẳng vuông góc với AN cắt đường thẳng CD tại Q. Gọi I là trung điểm của NQ. Gọi M là giao điểm AI và CD. Qua N dựng đường thẳng song song với CD cắt AI tại P. Chứng minh rằng:
a) ∆PIN = ∆MIQ.
b) Tứ giác MNPQ là hình thoi.
Lời giải:
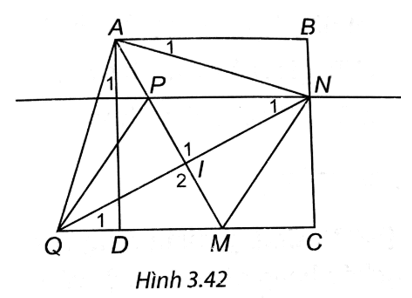
(H.3.42). a) Xét hai tam giác PIN và MIQ có (hai góc đối đỉnh), QI = IN, (do NP // QM)
⇒ ∆PIN = ∆MIQ (g.c.g)
⇒ QM = NP.
b) Tứ giác MNPQ có PN // MQ, QM = NP nên là hình bình hành.
Ta chứng minh MNPQ có hai đường chéo vuông góc.
Vì AQ ⊥ AN nên
Xét hai tam giác vuông ADQ và ABN có AD = AB, (chứng minh trên).
⇒ ∆ADQ = ∆ABN (cạnh góc vuông – góc nhọn)
⇒ AQ = AN.
Do đó tam giác AQN cân tại A, mà AI là đường trung tuyến của tam giác AQN
⇒ AI là đường cao của tam giác AQN, tức là AI ⊥ QN, hay PM ⊥ QN.
Hình bình hành MNPQ có hai đường chéo PM ⊥ QN nên là hình thoi.
Xem thêm lời giải Vở thực hành Toán 8 Kết nối tri thức hay, chi tiết khác:
Xem thêm Lời giải bài tập Vở thực hành Toán 8 Kết nối tri thức hay, chi tiết khác:
Bài 14: Hình thoi và hình vuông
Bài 15: Định lí Thalès trong tam giác
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.