Toptailieu.vn biên soạn và giới thiệu giải Giải Vở thực hành Toán 8 (Kết nối tri thức) Bài 15: Định lí Thalès trong tam giác hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm các bài tập từ đó nâng cao kiến thức và biết cách vận dụng phương pháp giải vào các bài tập Toán 8. Mời các bạn cùng đón xem:
Giải Vở thực hành Toán 8 (Kết nối tri thức) Bài 15: Định lí Thalès trong tam giác
Câu 1 trang 69 vở thực hành Toán 8 Tập 1: Quan sát Hình 4.1 biết MN // BC. Tỉ số bằng
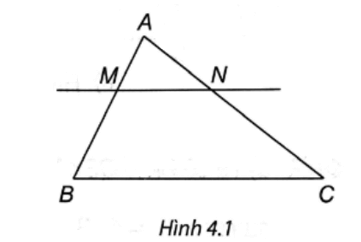
A.
B.
C.
D.
Lời giải:
Đáp án đúng là: B
Áp dụng định lí Thalès, MN // BC ⇒
Câu 2 trang 69 vở thực hành Toán 8 Tập 1: Quan sát Hình 4.2 và chọn khẳng định đúng.
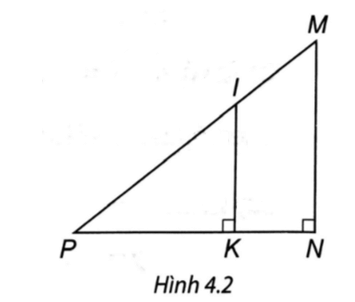
A.
B.
C.
D.
Lời giải:
Đáp án đúng là: C
Ta có IK ⊥ PN, MN ⊥ PN ⇒ IK // MN.
Áp dụng định lí Thales, ta có:
Câu 3 trang 70 vở thực hành Toán 8 Tập 1: Cho AB = 10 cm; MN = 3 dm. Tỉ số nào đúng?
A.
B.
C.
D.
Lời giải:
Đáp án đúng là: C.
Đổi 3 dm = 10 cm
Do đó
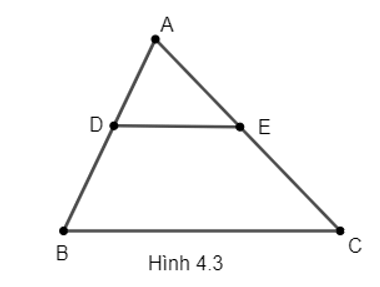
Quan sát Hình 4.3. Biết DE song song BC, AD = 12, DB = 18, CE = 30
A. 20.
B. 56.
C. 45.
D. 50.
Lời giải:
Đáp án đúng là: D.
Áp dụng định lí Thales, ta có:
Mà AB = AD + DB = 12 + 18 = 30
Khi đó hay .
Do đó AC = 50.
A.
B.
C.
D.
Lời giải:
Đáp án đúng là: A.
Tỉ số chu vi tam giác AMN và tam giác ABC là:
Áp dụng định lí Thales, ta có: mà
Do đó
Áp dụng dãy tỉ số bằng nhau, suy ra
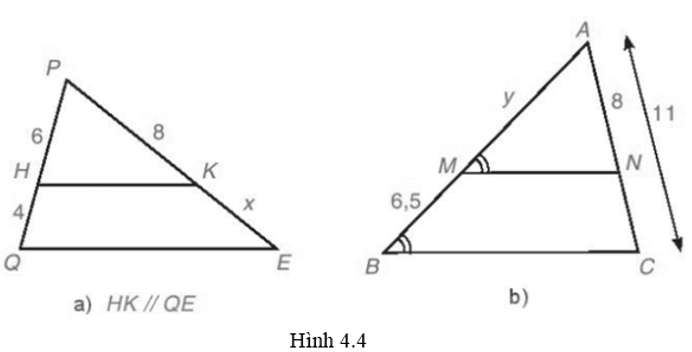
Lời giải:
a) Ta có HK // QE nên theo định lí Thales ta có: nên
suy ra 6 . x = 4 . 8
x ≈ 5,3.
b) Ta có mà hai góc này ở vị trí đồng vị nên MN // BC.
Theo định lí Thales ta có: nên
suy ra y . 3 = 8 . 6,5
y ≈ 17,3.
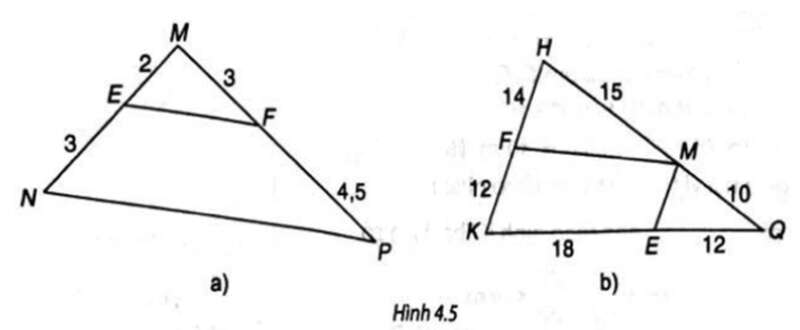
Lời giải:
a) Ta có suy ra EF // NP (định lí Thales đảo).
b) Ta có suy ra ME // HK (định lí Thales đảo).
Lời giải:
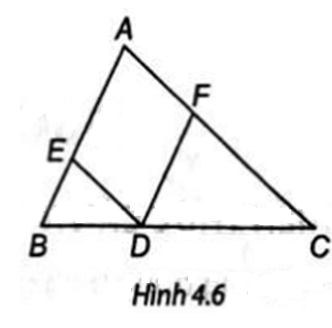
Ta có ED // AC suy ra (định lí Thales trong tam giác)
FD // AB suy ra (định lí Thales trong tam giác).
Suy ra
Lời giải:
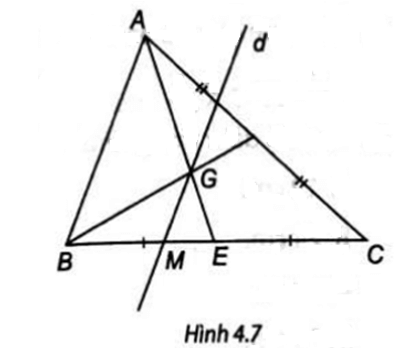
AG cắt BC tại E.
Ta có GM // AB suy ra (định lí Thales).
Ta lại có (G là trọng tâm ∆ABC) nên
Suy ra
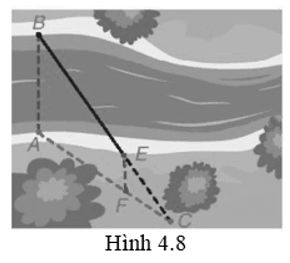
Lời giải:
Ta có AB // EF nên theo định lí Thales ta có: nên suy ra EB . 20 = 40 . 30, do đó EB = 60 (m).
Lời giải:
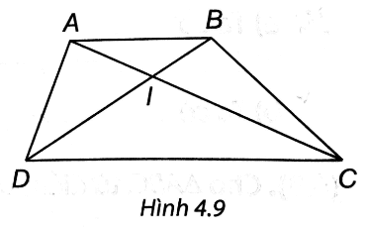
Ta có AB // DC nên theo định lí Thales ta có: nên IA . ID = IB . IC.
Xem thêm Lời giải bài tập Vở thực hành Toán 8 Kết nối tri thức hay, chi tiết khác:
Bài 16: Đường trung bình của tam giác
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.