Toptailieu.vn biên soạn và giới thiệu giải Giải Vở thực hành Toán 8 (Kết nối tri thức) Bài Luyện tập chung trang 77 hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm các bài tập từ đó nâng cao kiến thức và biết cách vận dụng phương pháp giải vào các bài tập Toán 8. Mời các bạn cùng đón xem:
Giải Vở thực hành Toán 8 (Kết nối tri thức) Bài Luyện tập chung trang 77
Bài 1 trang 77 vở thực hành Toán 8 Tập 1: Tìm độ dài x trong Hình 4.25.
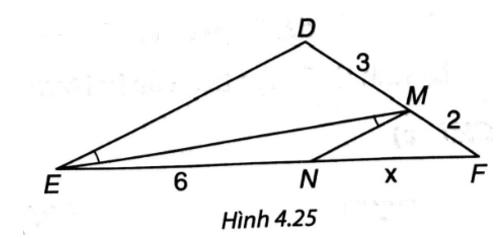
Lời giải:
Ta có Hai góc này ở vị trí so le trong nên DE // MN.
∆DEF có MN // DE nên theo định lí Thales ta có: hay suy ra x = 4.
a) Chứng minh EK // CD, FK // AB.
b) So sánh EF và
Lời giải:
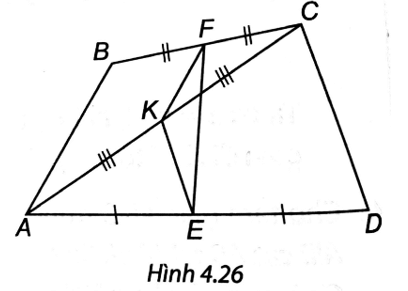
a) ∆ABC có F là trung điểm BC, K là trung điểm AC nên FK là đường trung bình của ∆ABC, suy ra FK // AB.
∆ACD có E là trung điểm AD nên EK là đường trung bình của ∆ACD, suy ra EK // CD.
b) FK là đường trung bình của ∆ABC nên AB = 2FK.
Tương tự CD = 2EK.
Ta có FK + KE ≥ FE nên ≥ EF.
Do đó EF ≤
Lời giải:
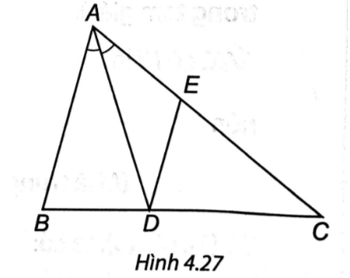
AD là đường phân giác của góc BAC.
Suy ra (tính chất đường phân giác trong tam giác). (1)
Ta có ED // AB suy ra (2)
Từ (1) và (2) ta có:
a) Tính độ dài các đoạn thẳng DB và DC.
b) Tính tỉ số diện tích của hai tam giác ABD và ACD.
Lời giải:
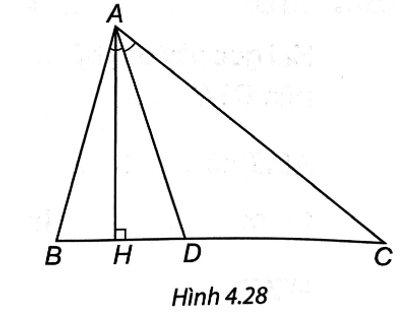
a) AD là phân giác của góc BAC, suy ra (tính chất đường phân giác của tam giác)
20.(25 – DC) = 15DC
35DC = 500
Suy ra DB = BC – DC ≈ 10,7 (cm).
b) Ta có
∆ABD và ∆ACD có cùng đường cao AH nên tỉ số diện tích của hai tam giác bằng tỉ số độ dài của hai cạnh đáy DB và DC.
Vậy tỉ số diện tích của hai tam giác ABD và ACD là
Lời giải:
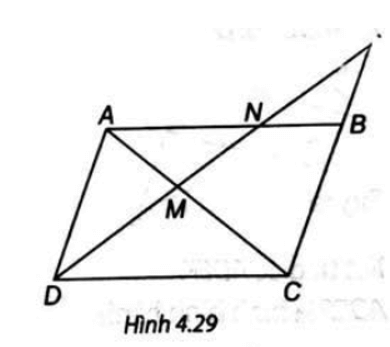
• AN // CD suy ra (định lí Thales trong tam giác).
• AD // CK suy ra (định lí Thales trong tam giác).
Suy ra
Do đó MD2 = MN . MK.
Xem thêm Lời giải bài tập Vở thực hành Toán 8 Kết nối tri thức hay, chi tiết khác:
Bài 17: Tính chất đường phân giác của tam giác
Bài 18: Thu thập và phân loại dữ liệu
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.