Với Giải Câu 2 trang 78 VTH Toán 8 Tập 1 lớp 8 trong Bài Luyện tập chung trang 77 Vở thực hành Toán 8 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong Vở thực hành Toán 8.
Cho tứ giác ABCD, gọi E, F, K lần lượt là trung điểm của AD, BC, AC
Bài 2 trang 78 vở thực hành Toán 8 Tập 1: Cho tứ giác ABCD, gọi E, F, K lần lượt là trung điểm của AD, BC, AC.
a) Chứng minh EK // CD, FK // AB.
b) So sánh EF và 12(AB+CD).
Lời giải:
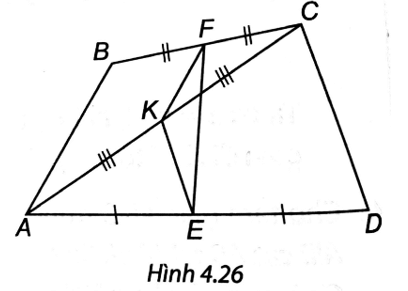
a) ∆ABC có F là trung điểm BC, K là trung điểm AC nên FK là đường trung bình của ∆ABC, suy ra FK // AB.
∆ACD có E là trung điểm AD nên EK là đường trung bình của ∆ACD, suy ra EK // CD.
b) FK là đường trung bình của ∆ABC nên AB = 2FK.
Tương tự CD = 2EK.
Ta có FK + KE ≥ FE nên 12(AB+CD). ≥ EF.
Do đó EF ≤ 12(AB+CD).
Xem thêm lời giải Vở thực hành Toán 8 Kết nối tri thức hay, chi tiết khác:
Bài 1 trang 77 vở thực hành Toán 8 Tập 1: Tìm độ dài x trong Hình 4.25.
Xem thêm Lời giải bài tập Vở thực hành Toán 8 Kết nối tri thức hay, chi tiết khác:
Bài 17: Tính chất đường phân giác của tam giác
Bài 18: Thu thập và phân loại dữ liệu
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.