Toptailieu.vn giới thiệu Giải sách bài tập Toán lớp 8 Bài 5: Diện tích hình thoi chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:
Giải SBT Toán 8 Bài 5: Diện tích hình thoi
Bài 42 Trang 162 SBT Toán 8 Tập 1 Trong những hình thoi có chu vi bằng nhau, hãy tìm hình thoi có diện tích lớn nhất.
Phương pháp giải:
Diện tích hình thoi bằng tích của cạnh đáy với chiều cao:
Lời giải:
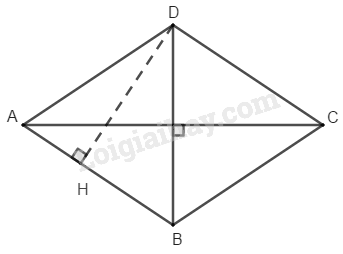
Xét hình thoi Kẻ
Ta có:
vuông tại
Suy ra: , mà (gt)
Vậy có giá trị lớn nhất khi bằng
Khi đó là hình vuông
Vậy trong các hình thoi có chu vi bằng nhau thì hình vuông là hình có diện tích lớn nhất.
Bài 43 Trang 163 SBT Toán 8 Tập 1 Tính diện tích hình thoi, biết cạnh của nó dài và một trong các góc của nó có số đo bằng
Phương pháp giải:
Diện tích hình thoi bằng tích của cạnh đáy với chiều cao:
Lời giải:
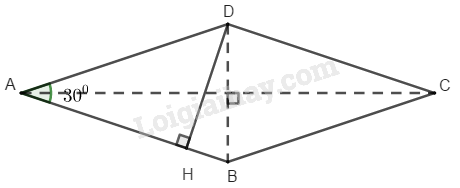
Giả sử hình thoi có
Từ kẻ ()
Tam giác vuông là một nửa tam giác đều cạnh AD
Bài 44 Trang 163 SBT Toán 8 Tập 1 Cho hình thoi biết ( là giao điểm của hai đường chéo). Hãy tính diện tích hình thoi đó.
Phương pháp giải:
Diện tích hình thoi bằng một nửa tích độ dài hai đường chéo:
Lời giải:
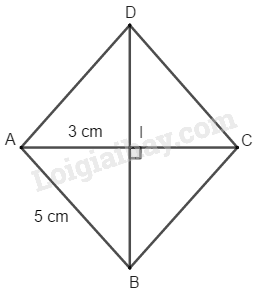
Vì ABCD là hình thoi nên và (tính chất)
Trong tam giác vuông ta có:
(định lý Pi-ta-go)
Bài 45 Trang 163 SBT Toán 8 Tập 1 a) Hãy vẽ một tứ giác có hai đường chéo vuông góc với nhau, biết độ dài hai đường chéo đó là và . Hỏi có thể vẽ được bao nhiêu hình như vậy ?
b) Có thể vẽ được mấy hình thoi, biết độ dài hai đường chéo là và ?
c) Hãy tính diện tích các hình vừa vẽ.
Phương pháp giải:
Diện tích hình thoi bằng một nửa tích độ dài hai đường chéo:
Lời giải:
a) Vẽ vô số hình tứ giác thỏa mãn yêu cầu.
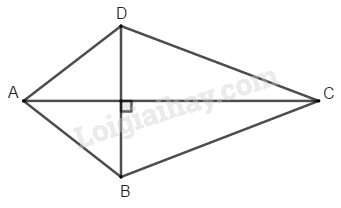
b) Vẽ được duy nhất một hình thoi có hai đường chéo là và
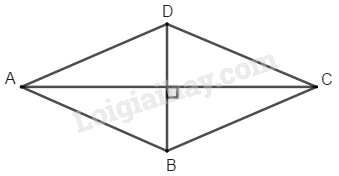
c) Diện tích các hình vẽ đó là : (đvdt)
Bài 46 Trang 163 SBT Toán 8 Tập 1 Hai đường chéo của một hình thoi có độ dài là và Tính:
a) Diện tích hình thoi
b) Độ dài cạnh hình thoi
c) Độ dài đường cao hình thoi
Phương pháp giải:
Diện tích hình thoi bằng một nửa tích độ dài hai đường chéo:
Diện tích hình thoi bằng tích của cạnh đáy với chiều cao:
Lời giải:
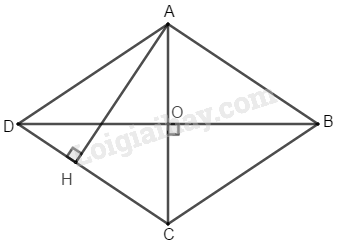
Giả sử ABCD là hình thoi có và O là giao điểm hai đường chéo
Suy ra và là trung điểm của AC, BD.
Do đó
a.
b.Trong tam giác vuông , theo định lý Pytago ta có:
Vậy cạnh hình thoi là .
c. Kẻ ()
Bài 5.1 Trang 163 SBT Toán 8 Tập 1 a) Sử dụng kéo cắt đúng hai lần, theo đường thẳng, chia một hình chữ nhật thành ba phần sao cho có thể ghép lại thành một hình thoi.
b) Sử dụng kéo cắt đúng hai lần, theo đường thẳng, chia một hình thoi thành ba phần sao cho có thể ghép lại thành một hình chữ nhật.
Từ đó suy ra công thức tính diện tích hình thoi dựa vào công thức tính diện tích hình chữ nhật.
Phương pháp giải:
Cắt ghép hình sao cho hợp lí.
Lời giải:
a) Giả sử có hình chữ nhật . Lấy điểm là trung điểm của cạnh
Cắt theo cạnh và Sau đó chuyển tam giác đến vị trí của tam giác chuyển tam giác đến vị trí của tam giác ta được hình thoi
Khi đó diện tích của hình thoi bằng diện tích của hình chữ nhật
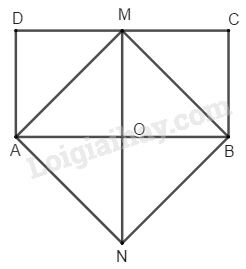
b) Ta chỉ cần thao tác ngược lại, chẳng hạn ta có hình thoi tâm , tiến hành cắt theo cắt theo khi đó chia được hình thoi thành ba phần là tam giác tam giác và tam giác , sau đó ghép lại thành hình chữ nhật
Từ đó suy ra: Diện tích hình thoi có số đo bằng một nửa tích độ dài hai đường chéo của nó.

Bài 5.2 Trang 163 SBT Toán 8 Tập 1 Cho tứ giác có hai đường chéo và vuông góc với nhau. Biết Gọi theo thứ tự là trung điểm các cạnh Gọi theo thứ tự là trung điểm các cạnh
a) Chứng minh rằng là hình chữ nhật.
b) Tính diện tích của tứ giác
Phương pháp giải:
Áp dụng tính chất đường trung bình của tam giác: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Lời giải:
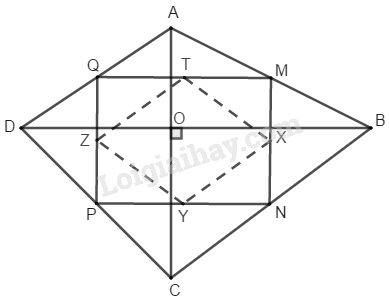
a) Trong ta có:
là trung điểm của
là trung điểm của
nên là đường trung bình của
và (tính chất đường trung bình của tam giác) (1)
Trong ta có:
là trung điểm của
là trung điểm của
nên là đường trung bình của
và (tính chất đường trung bình của tam giác) (2)
Từ (1) và (2) suy ra: và nên tứ giác là hình bình hành
(gt)
(chứng minh trên)
Suy ra:
Trong có là đường trung bình
Suy ra: hay
Vậy tứ giác là hình chữ nhật.
b) Kẻ đường chéo và
Trong ta có:
là trung điểm của
là trung điểm của
nên là đường trung bình của
và (tính chất đường trung bình của tam giác) (3)
Trong ta có:
là trung điểm của
là trung điểm của
nên là đường trung bình của
và (tính chất đường trung bình của tam giác) (4)
Từ (3) và (4) suy ra: và nên tứ giác là hình bình hành.
Trong ta có là đường trung bình
(tính chất đường trung bình của tam giác)
Tứ giác là hình chữ nhật
Suy ra: Vậy tứ giác là hình thoi
mà
Vậy :
Bài 5.3 Trang 163 SBT Toán 8 Tập 1 Cho tam giác vuông có hai cạnh góc vuông là và Trên cạnh lấy điểm sao cho Trên cạnh lấy điểm sao cho Gọi tương ứng là trung điểm của các đoạn thẳng và Tính diện tích của tứ giác
Phương pháp giải:
Áp dụng tính chất đường trung bình của tam giác: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Lời giải:
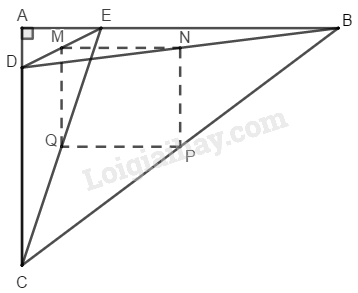
+) Trong ta có:
là trung điểm của
là trung điểm của
nên là đường trung bình của
và
+) Trong ta có:
là trung điểm của
là trung điểm của
nên là đường trung bình của
+) Trong ta có:
là trung điểm của
là trung điểm của
nên là đường trung bình của
và
+) Trong ta có:
là trung điểm của
là trung điểm của
nên là đường trung bình của
Suy ra: (1)
hay
(do tam giác ABC vuông tại A)
Lại có: hay
Suy ra: hay (2)
Từ (1) và (2) suy ra tứ giác là hình vuông
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.