Toptailieu.vn giới thiệu Giải sách bài tập Toán lớp 8 Bài 6: Diện tích đa giác chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:

Giải SBT Toán 8 Bài 6: Diện tích đa giác

Bài 47 Trang 164 SBT Toán 8 Tập 1 Thực hiện các phép vẽ và đo cần thiết để tính diện tích đa giác $ABCDE$ $(BE//CD)$ (h.189)

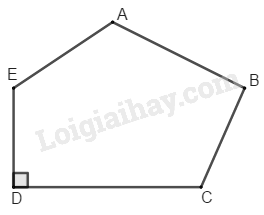
Phương pháp giải:

Chia hình đã cho thành hình tam giác và hình thang, sau đó thực hiện đo độ dài để tính diện tích hình đã cho.

Lời giải:

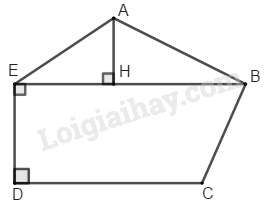
Chia đa giác $ABCDE$ thành $∆ABE$ và hình thang vuông $BEDC.$

Kẻ $AH\perp BE.$ Dùng thước chia khoảng đo độ dài: $BE,DE,CD,AH.$

Thực hiện đo độ dài ta được: $BE=3,6cm;DE=1,3cm,$$DC=2,7cm,AH=1,1cm$

$S_{ABCDE}=S_{ABE}+S_{BEDC}$

$\begin{array}{l}={\displaystyle \frac{1}{2}}AH.EB+{\displaystyle \frac{1}{2}}\left(DC+EB\right).ED\\ ={\displaystyle \frac{1}{2}}.1,1.3,6+{\displaystyle \frac{1}{2}}\left(2,7+3,6\right).1,3\\ =6,075c{m}^2\end{array}$

Bài 48 Trang 164 SBT Toán 8 Tập 1 Theo bản đồ và tỉ lệ ghi trên hình 190, hãy tính diện tích của hồ nước (phần bị gạch sọc).

Phương pháp giải:

Ta chia hình đã cho thành các hình tam giác, hình thang sao cho hợp lí rồi đo các đoạn và tính diện tích của hồ nước.

Lời giải:

Đặt tên hình chữ nhật là $ABCD.$

Trên cạnh $AB,$ $2$ giao điểm là $E$ và $G.$

Trên $BC$ hai giao điểm là $I$ và $H$

Trên $CD$ hai giao điểm là $L$ và $M.$ Giao điểm trên $AD$ là $N.$ Hình thang tại đỉnh $B$ có giao điểm là $P,$ điểm trên đường gấp khúc $IL$ là $K$

Kẻ $KQ\perp CD,$ gọi diện tích phần gạch sọc là $S$

Ta có:$$\begin{gathered} S=S_{ABCD}-S_{ANE}-S_{BHPG}-S_{ICQK} \\ -S_{LQK}-S_{DMN} \end{gathered}$$

Dùng thước chia khoảng đo các đoạn $(mm):$

$AB,AD,AE,AN,PG,GB,BH,$$IC,CQ,QK,LQ,DM$

Ta được:

$\begin{array}{l}AB=49mm,AD=24mm,AE=14mm,\\ AN=5mm,BG=14mm,BH=7mm,\\ IC=11cm,CQ=9mm,QK=6mm,\\ LQ=25mm,DM=7mm,\\ DN=19mm,PG=3mm\end{array}$

Ta có: 

$\begin{array}{l}{S}_{ABCD}=AB.AD=49.24=1176\\ S_{AEN}={\displaystyle \frac{1}{2}}AE.AN={\displaystyle \frac{1}{2}}.14.5=35\end{array}$

$S_{BHPG}={\displaystyle \frac{1}{2}}\left(PG+BH\right).BG$$={\displaystyle \frac{1}{2}}\left(3+7\right).14=70$

$S_{ICQK}={\displaystyle \frac{1}{2}}\left(KQ+IC\right).QC$$={\displaystyle \frac{1}{2}}\left(6+11\right).9=76,5$

$\begin{array}{l}{S}_{LQK}={\displaystyle \frac{1}{2}}KQ.LQ={\displaystyle \frac{1}{2}}.6.25=75\\ S_{DMN}={\displaystyle \frac{1}{2}}DN.DM={\displaystyle \frac{1}{2}}.19.7=66,5\end{array}$

Khi đó: 

 $$\begin{gathered} S=S_{ABCD}-S_{ANE}-S_{BHPG}-S_{ICQK} \\ -S_{LQK}-S_{DMN} \end{gathered}$$

$=853m{m}^2$

Vì tỉ lệ là ${\displaystyle \frac{1}{100}}$ nên thực tế diện tích hồ nước là: $853.100=85300m{m}^2=8,53d{m}^2$

Bài 49 Trang 164 SBT Toán 8 Tập 1 Theo kích thước đã cho trên hình 191, hãy tính diện tích hình gạch sọc (đơn vị $m^2$ ).

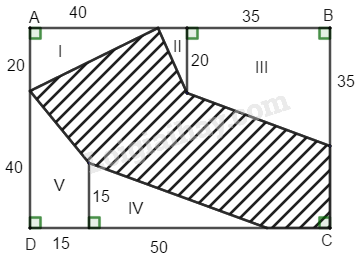
Phương pháp giải:

Áp dụng công thức tính diện tích hình tam giác bằng nửa tích cạnh và chiều cao tương ứng:$S={\displaystyle \frac{1}{2}}ab$ và công thức tính diện tích hình thang bằng nửa tích hai đáy với chiều cao: $S={\displaystyle \frac{a+b}{2}}.h$ 

Lời giải:

$\begin{array}{l}{S}_{ABCD}=AD.AB\\ =(20+40).(40+10+35)\\ =5100(m^2)\\ S_I={\displaystyle \frac{1}{2}}.40.20=400(m^2)\\ S_{II}={\displaystyle \frac{1}{2}}.10.20=100(m^2)\\ S_{III}={\displaystyle \frac{1}{2}}.(20+35).35=962,5(m^2)\\ S_{IV}={\displaystyle \frac{1}{2}}.15.50=375(m^2)\\ S_V={\displaystyle \frac{1}{2}}.(15+40).15=412,5(m^2)\end{array}$

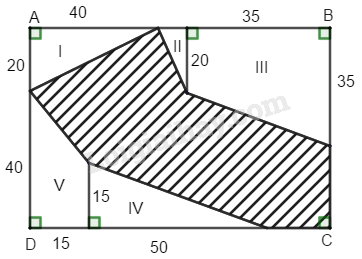
Diện tích phần gạch sọc :

$S=5100–(400+100+962,5+375$ $+412,5)=2850(m^2)$

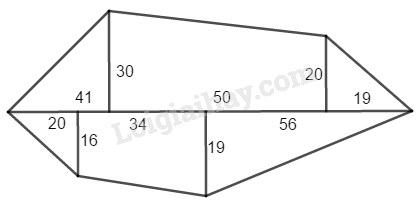
Bài 50 Trang 164 SBT Toán 8 Tập 1 Tìm diện tích mảnh đất theo kích thước cho trên hình 192 (đơn vị $m^2$)

Phương pháp giải:

Áp dụng công thức tính diện tích hình tam giác bằng nửa tích cạnh và chiều cao tương ứng:$S={\displaystyle \frac{1}{2}}ab$ và công thức tính diện tích hình thang bằng nửa tích hai đáy với chiều cao: $S={\displaystyle \frac{a+b}{2}}.h$

Lời giải:

$\begin{array}{rl}& S_I=\frac{1}{2}.41.30=615(m^2)\\ & S_{II}=\frac{1}{2}.\left(30+20\right).50=1250(m^2)\\ & S_{III}=\frac{1}{2}.20.19=190(m^2)\\ & S_{IV}=\frac{1}{2}.19.56=532(m^2)\\ & S_V=\frac{1}{2}.\left(19+16\right).34=595(m^2)\\ & S_{VI}=\frac{1}{2}.16.20=160(m^2)\end{array}$  

$\begin{array}{l}S=S_I+S_{II}+S_{III}+S_{IV}+S_V\\ +S_{VI}\\ =615+1250+190+532+595\\ +160=3342(m^2)\end{array}$

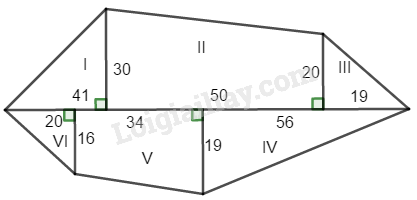
Bài 6.1 Trang 164 SBT Toán 8 Tập 1 Tính diện tích của hình được cho trong mỗi trường hợp sau đây:

a) Đa giác $ABCDEF,$ biết $AD=4cm,$ $BC=1cm,FE=2cm,FB=3cm,$ $FB$ vuông góc với $AD$ như hình bs. 24

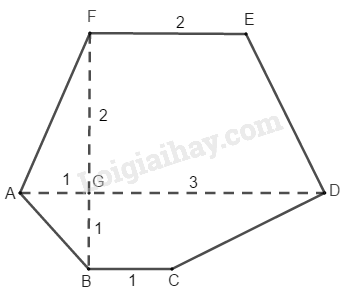
b) Cho đa giác $ABCD,CF$ và $DE$ đều vuông góc với $AB$ (như hình bs. 25)

Biết $AB=13cm,CF=8cm,$ $DE=4cm,FB=6cm$ và $AE=3cm.$ Tính diện tích đa giác $ABCD$

Phương pháp giải:

Chia đa giác đã cho thành các hình thang và tam giác.

Dựa vào công thức diện tích tam giác và hình thang tính được diện tích của mỗi hình đó.

Áp dụng công thức tính diện tích hình tam giác bằng nửa tích cạnh và chiều cao tương ứng: $S={\displaystyle \frac{1}{2}}ab$ và công thức tính diện tích hình thang bằng nửa tích hai đáy với chiều cao: $S={\displaystyle \frac{a+b}{2}}.h$ 

Sau đó suy ra được diện tích của đa giác đã cho.

Lời giải:

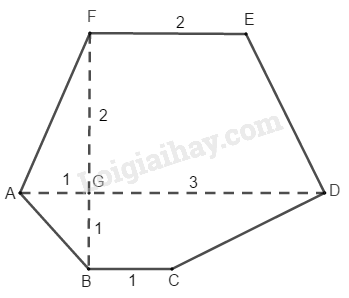
a) Ta chia đa giác $ABCDEF$ thành hai hình thang $ABCD$ và $ADEF.$

Hình thang $ABCD$ có cạnh đáy $BC=1(cm)$

Đáy $AD=AG+GD=1+3=4$ $(cm)$

Đường cao $BG=1$ $(cm)$

$\begin{array}{r}{S}_{ABCD}\end{array}=\begin{array}{r}\frac{AD+BC}{2}\end{array}.FG$ $=\begin{array}{r}\frac{4+1}{2}\end{array}=\begin{array}{r}\frac{5}{2}\end{array}$ (cm²)

Hình thang $ADEF$ có đáy $AD=4$ $(cm)$

Đáy $EF=2cm,$ đường cao $FG=2cm$

$\begin{array}{r}{S}_{ADEF}\end{array}=\begin{array}{r}\frac{AD+EF}{2}\end{array}.FG$ $=\begin{array}{r}\frac{4+2}{2}\end{array}.2=\begin{array}{r}6\end{array}(c{m}^2)$

$\begin{array}{r}{S}_{ABCDEF}\end{array}=S_{ABCD}+S_{ADEF}$

$\begin{array}{r}=\end{array}\begin{array}{r}\frac{5}{2}\end{array}+6=\begin{array}{r}\frac{17}{2}\end{array}(c{m}^2)$

b)

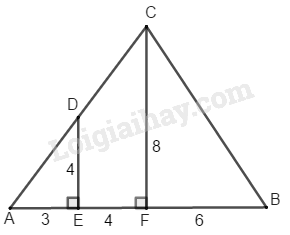
Chia đa giác $ABCD$ thành tam giác vuông $AED,$ hình thang vuông $EDCF$ và tam giác vuông $FCB.$

$\begin{array}{r}{S}_{AED}\end{array}={\displaystyle \frac{1}{2}AE.DE}$ $=\begin{array}{r}\frac{1}{2}\end{array}.3.4=6(c{m}^2)$ 

$\begin{array}{r}{S}_{EDCF}\end{array}=\begin{array}{r}\frac{ED+FC}{2}\end{array}.EF$

$=\begin{array}{r}\frac{4+8}{2}\end{array}.4=24(c{m}^2)$

$$\begin{gathered} \begin{array}{r}{S}_{CFB}\end{array}=\begin{array}{r}\frac{1}{2}\end{array}CF.FB \\ =\begin{array}{r}\frac{1}{2}\end{array}.8.6=24(c{m}^2) \end{gathered}$$

$$\begin{gathered} \begin{array}{r}{S}_{ABCD}\end{array}=S_{AED}+S_{EDCF}+S_{CFB} \\ =6+24+24=54(c{m}^2) \end{gathered}$$

Bài 6.2 Trang 164 SBT Toán 8 Tập 1 Cho hình bình hành $ABCD,$ với diện tích $S$ và $AB=a,AD=b.$ Lấy mỗi cạnh của hình bình hành đó làm cạnh dựng một hình vuông ra phía ngoài hình bình hành. Tính theo $a,b$ và $S$ diện tích của đa giác giới hạn bởi các cạnh của hình vuông mà không là cạnh của hình bình hành đã cho.

Phương pháp giải:

Tính diện tích các hình vuông rồi sau đó tính diện tích hình đa giác đã cho. 

Diện tích hình vuông cạnh $a$ bằng $a^2$

Lời giải:

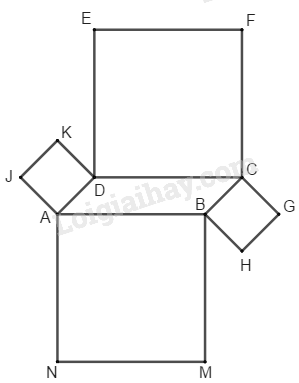
Hình đa giác đó gồm hình bình hành $ABCD,$ hình vuông $ABMN,BHGC,$ $CFED,DKJA.$

Ta có: 

$\begin{array}{rl}& S_{ABMN}=S_{CDEF}=a^2\\ & S_{BHGC}=S_{DKJA}=b^2\end{array}$

Gọi diện tích của đa giác cần tìm là $S^{\prime }$

Diện tích đa giác là:

$S^{\prime }=S+S_{ABMN}+S_{CDEF}+S_{BHGC}$ $+S_{DKJA}$

$=S+a^2+a^2+b^2+b^2$

$=S+2(a^2+b^2)$

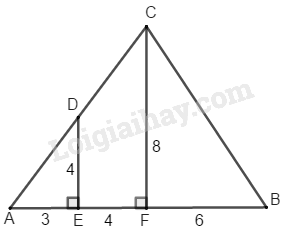
Bài 6.3 Trang 164 SBT Toán 8 Tập 1 Bạn Giang đã vẽ một đa giác $ABCDEFGHI$ như ở hình bs. 26.

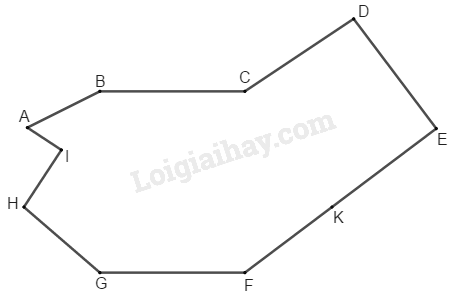
Tính diện tích của đa giác đó, biết rằng: $KH$ song song với $BC$ ($K$ thuộc $EF$); $BC$ song song với $GF;$ $CF$ song song với $BG;BG$ vuông góc với $GF;CK$ song song với $DE;CD$ song song với $FE;KE=DE$ và $KE$ vuông góc với $DE;I$ là trung điểm của $BH,AI=IH$ và $AI$ vuông góc với $IH;HK=11cm.$ $HK$ cắt $CF$ tại $J$ và $JK=3(cm),$ $CJ=4cm.$ $BG$ cắt $HK$ tại $M$ và $HM=2cm.$

Phương pháp giải:

Chia hình đa giác đã cho thành các hình vuông, hình thang và hình tam giác. Áp dụng công thức tính diện tích hình vuông, hình thang và hình tam giác để tính.

Áp dụng công thức:

Diện tích hình tam giác bằng nửa tích cạnh và chiều cao tương ứng: $S={\displaystyle \frac{1}{2}}ab$

Diện tích hình thang bằng nửa tích hai đáy với chiều cao: $S={\displaystyle \frac{a+b}{2}}.h$

Diện tích hình vuông cạnh $a$ bằng $a^2$ 

Lời giải:

Chia đa giác đó thành hình vuông $CDEK,$ hình thang $KFGH,$ hình thang $BCKH$ và tam giác vuông $AIB$

Ta có: $MJ=KH–KJ–MH$ $=11–2–3=6(cm)$

$\Rightarrow BC=GF=MJ=6(cm)$

$CJ=4(cm)$

$\begin{array}{r}{S}_{KFGH}=\frac{HK+GF}{2}.FJ\end{array}$ $=\begin{array}{r}\frac{11+6}{2}\end{array}.2=17(c{m}^2)$

$\begin{array}{r}{S}_{BCKH}=\frac{BC+KH}{2}.CJ\end{array}$ $=\begin{array}{r}\frac{11+6}{2}\end{array}.4=34(c{m}^2)$

Trong tam giác vuông $CJK$ có $\hat{J}={90}^{\circ }$. Theo định lý Pi-ta-go ta có:

$$\begin{gathered} C{K}^2=C{J}^2+J{K}^2=16+9=25 \\ \Rightarrow CK=5 \end{gathered}$$$(cm)$

$S_{CDEK}=C{K}^2=5^2=25$ $(c{m}^2)$

Trong tam giác vuông $BMH$ có $\hat{M}={90}^{\circ }$. Theo định lý Pi-ta-go ta có:

$B{H}^2=B{M}^2+H{M}^2$

mà $BM=CJ=4(cm)$ (đường cao hình thang $BCKH$)

$\begin{array}{rl}& \Rightarrow B{H}^2=4^2+2^2=20\end{array}$ $\Rightarrow \begin{array}{r}IB=\frac{BH}{2}\Rightarrow I{B}^2=\frac{B{H}^2}{4}\end{array}$ $\begin{array}{r}=\frac{20}{4}=5\end{array}$

Suy ra $IB=\sqrt{5}(cm)$

$∆AIB$ vuông cân tại $I$ (vì $AI=IH=IB$)

$S_{AIB}=\begin{array}{r}\frac{1}{2}\end{array}AI.IB=\begin{array}{r}\frac{1}{2}\end{array}I{B}^2=\begin{array}{r}\frac{5}{2}\end{array}$ $(c{m}^2)$

$S=S_{CDEK}+S_{KFGH}+S_{BCKH}$ $+S_{AIB}=25+17+34+\begin{array}{r}\frac{5}{2}\end{array}=\begin{array}{r}\frac{157}{2}\end{array}$ $(c{m}^2)$