Toptailieu.vn giới thiệu Giải sách bài tập Toán lớp 8 Bài 3: Diện tích tam giác chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:
Giải SBT Toán 8 Bài 3: Diện tích tam giác
Bài 25 Trang 159 SBT Toán 8 Tập 1 Hai đường chéo của hình chữ nhật chia hình chữ nhật thành bốn tam giác. Diện tích của các tam giác đó có bằng nhau không? Vì sao?
Phương pháp giải:
Chứng minh các tam giác bằng nhau, từ đó suy ra diện tích của các tam giác đó bằng nhau.
Lời giải:
Gọi là giao điểm hai đường chéo hình chữ nhật
(tính chất hình chữ nhật)
(1)
(2)
Kẻ
Suy ra: (3)
Từ (1), (2) và (3) suy ra:
Bài 26 Trang 159 SBT Toán 8 Tập 1 Cho tam giác có đáy cố định và đỉnh di động trên một đường thẳng cố định song song với đường thẳng Chứng minh rằng tam giác luôn có diện tích không đổi.
Phương pháp giải:
Áp dụng công thức tính diện tích tam giác: với lần lượt là chiều cao và cạnh đáy tương ứng.
Lời giải:
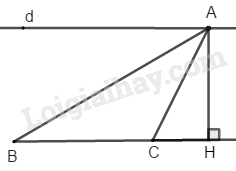
Đường thẳng d cố định song song với đường thẳng BC cố định nên khoảng cách hai đường thẳng d và BC là không đổi.
có đáy không đổi, chiều cao là khoảng cách giữa hai đường thẳng song song không đổi. Vậy điểm thay đổi trên đường thẳng thì không đổi.
Bài 27 Trang 159 SBT Toán 8 Tập 1 Tam giác có đáy cố định và dài Đỉnh di chuyển trên đường thẳng (). Gọi là chân đường cao hạ từ đỉnh xuống đường thẳng
a. Điền vào ô trống trong bảng sau:

b) Vẽ đồ thị biểu diễn số đo theo độ dài AH
c) Diện tích tam giác ABC có tỉ lệ thuận với chiều cao AH không?
Phương pháp giải:
Áp dụng công thức tính diện tích tam giác: với là chiều cao tương ứng với cạnh đáy .
Lời giải:
a) Ta có
Ta có bảng sau:

b) là hàm số của chiều cao
Gọi là diện tích của và độ dài là độ dài (cm) thì
Ta có đồ thị như hình sau:
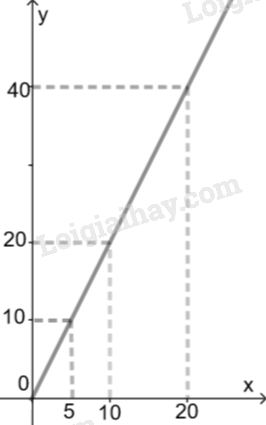
c) Diện tích của tam giác tỉ lệ thuận với chiều cao vì ( với k = 2 không đổi)
Bài 28 Trang 160 SBT Toán 8 Tập 1 Tính diện tích của hình 186 theo các kích thước đã cho trên hình ( có cùng đơn vị đo).
Phương pháp giải:
Chia hình đã cho thành hình tam giác và hình chữ nhật.
Diện tích tam giác bằng nửa tích chiều cao với cạnh đáy tương ứng
Diện tích hình chữ nhật bằng tích chiều dài với chiều rộng
Lời giải:
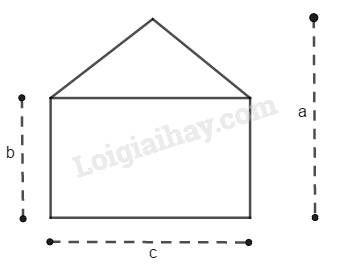
Diện tích phần là hình chữ nhật là:
(đơn vị diện tích)
Phần hình tam giác có cạnh đáy là và chiều cao tương ứng là
Diện tích phần hình tam giác là:
(đơn vị diện tích)
Diện tích hình vẽ đó là:
(đơn vị diện tích)
Bài 29 Trang 160 SBT Toán 8 Tập 1 Hai cạnh của một tam giác có độ dài là và Hỏi diện tích của tam giác đó có thể lấy giá trị nào trong các giá trị sau:
a)
b)
c)
Phương pháp giải:
Áp dụng công thức tính diện tích tam giác:
Tính chất của đường vuông góc và đường xiên.
Lời giải:
Giả sử hai cạnh của tam giác là và Diện tích của tam giác tính theo hai cạnh khác nhau là:
hoặc
(với và là đường cao ứng với cạnh đáy là và của hai tam giác.)
Theo tính chất của đường vuông góc và đường xiên thì ta có và
Suy ra diện tích của tam giác là: hay
Vậy diện tích của tam giác có thể bằng hoặc nhưng không thể bằng
Bài 30 Trang 160 SBT Toán 8 Tập 1 Cho tam giác biết Tính tỉ số hai đường cao xuất phát từ các đỉnh và
Phương pháp giải:
Áp dụng công thức tính diện tích tam giác: với lần lượt là độ dài chiều cao và cạnh đáy tương ứng.
Lời giải:
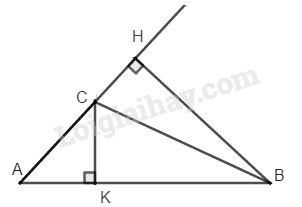
Trong tam giác kẻ đường cao và
Ta có:
Suy ra:
Mà (gt)
Vậy đường cao dài gấp lần đường cao
Bài 31 Trang 160 SBT Toán 8 Tập 1 Các điểm chia mỗi cạnh hình vuông thành ba đoạn thẳng bằng nhau. Gọi là giao điểm của và với và (h.187). Tính diện tích của ngũ giác và của tứ giác biết
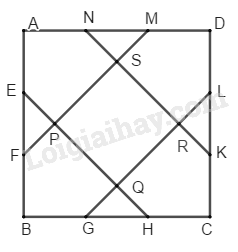
Phương pháp giải:
Biết diện tích hai tam giác vuông và thì tính được diện tích còn lại. Diện tích còn lại được chia thành năm phần bằng nhau, từ đó diện tích ngũ giác là một phần rưỡi và diện tích của tứ giác là hai phần.
Lời giải:
Diện tích hình vuông bằng ()
Diện tích tam giác bằng:
()
Diện tích tam giác bằng: ()
Diện tích phần còn lại là : ()
Trong tam giác vuông , theo định lý Pytago ta có:
Trong tam giác vuông , theo định lý Pytago ta có:
Diện tích hình chữ nhật bằng ()
Nối đường chéo Théo tính chất đường thẳng song song cách đều ta có hình chữ nhật được chia thành phần bằng nhau nên diện tích tứ giác chiếm phần và bằng 8
Diện tích bằng
Vậy
()
Bài 3.1 Trang 160 SBT Toán 8 Tập 1 a) Có thể dùng kéo cắt hai lần và chỉ cắt theo đường thẳng chia một tam giác (thường) thành ba mảnh để ghép lại được một hình chữ nhật hay không ?
Từ đó suy ra công thức tính diện tích tam giác thường dựa vào công thức tính diện tích hình chữ nhật.
b) Hãy chia một tam giác thành phần có diện tích bằng nhau bởi một đường thẳng đi qua đỉnh của tam giác đó.
c) Hãy chia một tam giác thành phần có diện tích bằng nhau bởi ba đường thẳng, trong đó chỉ có một đường đi qua đỉnh của tam giác đó.
Phương pháp giải:
Dựa vào công thức tính diện tích tam giác: với lần lượt là độ dài cạnh đáy và chiều cao tương ứng.
Lời giải:
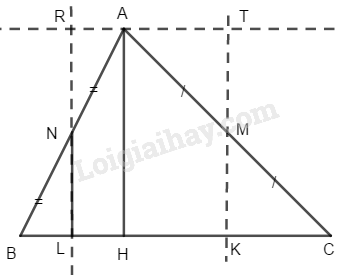
a) Xét Kẻ đường cao Gọi là trung điểm của là trung điểm của
Từ kẻ đường thẳng song song cắt tại
Từ kẻ đường thẳng song song cắt tại
Từ kẻ đường thẳng song song cắt hai đường thẳng và tại và
Ta có: (g-c-g)
(g-c-g)
Cắt theo đường và ta ghép lại được một hình chữ nhật có diện tích bằng diện tích tam giác
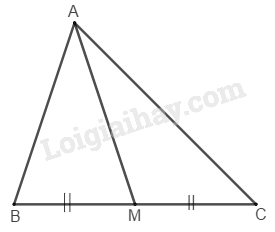
b) Ta đã biết hai tam giác có cạnh đáy bằng nhau và chung chiều cao thì có diện tích bằng nhau. Giả sử Gọi là trung điểm của
Cắt tam giác theo đường chia tam giác ra hai phần có diện tích bằng nhau.
c) Tương tự như trên câu b.
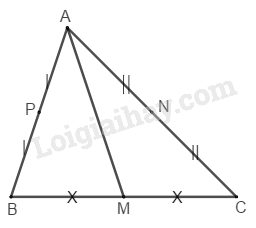
Xét Gọi là trung điểm của
là trung điểm của là trung điểm của
Cắt tam giác theo đường ta có hai phần có diện tích bằng nhau
Cắt tam giác theo đường ta có hai phần có diện tích bằng nhau
Cắt tam giác theo đường ta có hai phần diện tích bằng nhau, ta có diện tích bốn phần chia bằng nhau.
Bài 3.2 Trang 161 SBT Toán 8 Tập 1 Cho tam giác đều và điểm bất kì nằm trong tam giác đó. Đường thẳng đi qua điểm và vuông góc với tại điểm Đường thẳng đi qua điểm và vuông góc với tại điểm Đường thẳng đi qua điểm và vuông góc với tại điểm
Chứng minh rằng không phụ thuộc vào vị trí của điểm
Phương pháp giải:
Gợi ý: Tổng diện tích của tam giác bằng diện tích của tam giác
Lời giải:
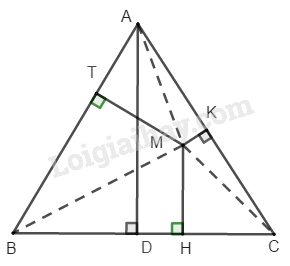
Giả sử đều có cạnh bằng kẻ đường cao đặt không đổi.
Ta có:
không đổi
Vậy tổng không phụ thuộc vào điểm
Bài 3.3 Trang 161 SBT Toán 8 Tập 1 a) Cho hai tam giác và Kẻ đường cao của tam giác Kẻ đường cao của tam giác Gọi là diện tích của tam giác Gọi là diện tích của tam giác
Chứng minh rằng
b) Cho tam giác và điểm bất kì nằm trong tam giác đó. Kẻ các đường cao của tam giác đó là và Đường thẳng đi qua điểm và song song với cắt cạnh tại điểm Đường thẳng đi qua điểm và song song với cắt cạnh tại điểm Đường thẳng đi qua điểm và song song với cắt cạnh tại điểm
Chứng minh rằng
Phương pháp giải:
Áp dụng công thức tính diện tích tam giác: với lần lượt là độ dài cạnh đáy và chiều cao tương ứng.
Lời giải:
a)
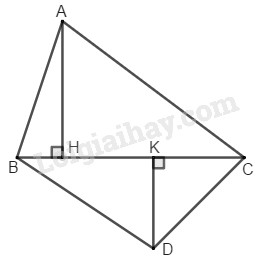
Ta thấy: và có chung canh đáy nên ta có:
Suy ra:
b)
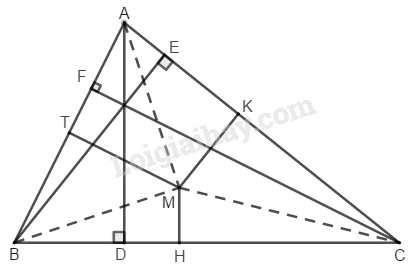
Gọi diện tích các hình tam giác lần lượt là Ta có:
Trong đó:
Từ đó, ta có:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.