Toptailieu.vn biên soạn và giới thiệu giải Sách bài tập Toán 11 Bài 2: Giới hạn của hàm số sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm các bài tập từ đó nâng cao kiến thức và biết cách vận dụng phương pháp giải vào các bài tập trong SBT Toán 11 Bài 2.
SBT Toán 11 (Cánh diều) Bài 2: Giới hạn của hàm số
Bài 12 trang 74 SBT Toán 11 Tập 1: Giả sử và (L, M ∈ ℝ). Phát biểu nào sau đây là sai?
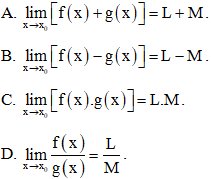
Lời giải:
Đáp án đúng là: D
Với và (L, M ∈ ℝ) thì (nếu M ≠ 0).
Do vậy đáp án D sai vì thiếu điều kiện M ≠ 0.
Bài 13 trang 74 SBT Toán 11 Tập 1: Cho hàm số y = f(x) xác định trên khoảng (x0; b). Phát biểu nào sau đây là đúng?
A. Nếu với dãy số (xn) bất kì, x0 < xn < b và xn → x0, ta có f(xn) → L thì .
B. Nếu với dãy số (xn) bất kì, xn → x0, ta có f(xn) → L thì .
C. Nếu với dãy số (xn) bất kì, x0 < xn < b và xn → L, ta có f(xn) → x0 thì .
D. Nếu với dãy số (xn) bất kì, xn < x0 và xn → x0, ta có f(xn) → L thì .
Lời giải:
Đáp án đúng là: A
Theo lí thuyết, ta có: Cho hàm số y = f(x) xác định trên khoảng (x0; b), nếu với dãy số (xn) bất kì, x0 < xn < b và xn → x0, ta có f(xn) → L thì .
Bài 14 trang 75 SBT Toán 11 Tập 1: Với c, k là các hằng số và k nguyên dương thì
A. .
B. .
C. .
D. hoặc .
Lời giải:
Đáp án đúng là: A
Với c, k là các hằng số và k nguyên dương, ta luôn có .
Bài 15 trang 75 SBT Toán 11 Tập 1: Phát biểu nào sau đây là đúng?
A. Nếu thì .
B. Nếu thì L ≥ 0.
c. Nếu f(x) ≥ 0 và thì L ≥ 0 và .
D. Nếu thì L ≥ 0 và .
Lời giải:
Đáp án đúng là: C
Theo lí thuyết ta có: Nếu f(x) ≥ 0 và thì L ≥ 0 và .
Bài 16 trang 75 SBT Toán 11 Tập 1: Cho hàm số y = f(x) xác định trên khoảng (a ; + ∞). Phát biểu nào sau đây là đúng?
A. Nếu với dãy số (xn) bất kì, xn > a và xn → +∞, ta có f(xn) → L thì .
B. Nếu với dãy số (xn) bất kì, xn < a và xn → +∞, ta có f(xn) → L thì .
C. Nếu với dãy số (xn) bất kì, xn > a, ta có f(xn) → L thì .
D. Nếu với dãy số (xn) bất kì, xn > a và xn → L, ta có f(xn) →+∞ thì .
Lời giải:
Đáp án đúng là: A
Theo lí thuyết, ta có: Cho hàm số y = f(x) xác định trên khoảng (a ; + ∞), nếu với dãy số (xn) bất kì, xn > a và xn → +∞, ta có f(xn) → L thì .
Bài 17 trang 75 SBT Toán 11 Tập 1: Sử dụng định nghĩa, chứng minh rằng:
a) .
b) .
Lời giải:
a) Xét hàm số f(x) = x3. Giả sử (xn) là dãy số bất kì, thỏa mãn limxn = – 2.
Ta có limf(xn) = .
Vậy .
b) Xét hàm số .
Giả sử (xn) là dãy số bất kì, thỏa mãn xn ≠ – 2 và lim xn = – 2.
Ta có .
Vậy .
Bài 18 trang 75 SBT Toán 11 Tập 1: Cho , chứng minh rằng:
a) ;
b) ;
c) .
Lời giải:
a) .
b) .
c) .
Bài 19 trang 76 SBT Toán 11 Tập 1: Quan sát đồ thị hàm số ở Hình 2 và cho biết các giới hạn sau: .
Lời giải:
Dựa vào đồ thị hàm số, ta có:
;
;
;
.
Bài 20 trang 76 SBT Toán 11 Tập 1: Tính các giới hạn sau:
a) ; b) ;
c) ; d) ;
e) ; g) .
Lời giải:
a) = – 4 – 3 + 1 = – 6.
b) .
c) Vì .
Do đó, .
d) Vì
và 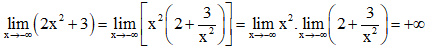
Do đó, .
e) Vì ; và x – 2 > 0 với mọi x > 2.
Do đó, .
g) Vì ; và x + 2 > 0 với mọi x > – 2.
Do đó, .
Bài 21 trang 76 SBT Toán 11 Tập 1: Tính các giới hạn sau:
a) ; b) ;
c) ; d) ;
e) ; g) .
Lời giải:
a) .
b) .
c)
d)
.
e) .
g) .
Bài 22 trang 76 SBT Toán 11 Tập 1: Cho . Tính:
a) ;
b) .
Lời giải:
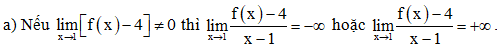
Điều này mâu thuẫn với giả thiết .
b) Ta có .
Bài 23 trang 76 SBT Toán 11 Tập 1: Cho hàm số f(x) thoả mãn . Tính .
Lời giải:
Ta có
.
Vậy .
Bài 24 trang 76 SBT Toán 11 Tập 1: Cho số thực a và hàm số (x) thoả mãn . Chứng minh rằng:
.
Lời giải:
Ta có
.
Vậy .
Bài 25 trang 76 SBT Toán 11 Tập 1: Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên biến đổi theo một hàm số thời gian (tính theo ngày) là g(t) = 45t2 – t3 (người). Tốc độ trung bình gia tăng người bệnh giữa hai thời điểm t1, t2 là . Tính và cho biết ý nghĩa của kết quả tìm được.
Lời giải:
Ta có g(10) = 45 . 102 – 103.
Khi đó
.
Vậy = 600.
Từ kết quả trên, ta thấy tốc độ tăng người bệnh ngay tại thời điểm t = 10 ngày là 600 người/ngày.
Xem thêm các bài SBT Toán 11 Cánh Diều hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.