Toptailieu.vn biên soạn và giới thiệu giải Sách bài tập Toán 11 Bài 3: Hàm số liên tục sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm các bài tập từ đó nâng cao kiến thức và biết cách vận dụng phương pháp giải vào các bài tập trong SBT Toán 11 Bài 3.

SBT Toán 11 (Cánh diều) Bài 3: Hàm số liên tục 

Bài 26 trang 80 SBT Toán 11 Tập 1: Phát biểu nào sau đây là đúng?

A. Hàm số y = f(x) liên tục tại x = a khi và chỉ khi $\underset{x\to a}{\lim }f\left(x\right)=f\left(a\right)$ .

B. Hàm số y = f(x) liên tục tại x = a khi và chỉ khi $\underset{x\to a^{-}}{\lim }f\left(x\right)=f\left(a\right)$ .

C. Hàm số y = f(x) liên tục tại x = a khi và chỉ khi $\underset{x\to a^{+}}{\lim }f\left(x\right)=f\left(a\right)$ .

D. Hàm số y = f(x) liên tục tại x = a khi và chỉ khi $\underset{x\to a^{-}}{\lim }f\left(x\right)=\underset{x\to a^{+}}{\lim }f\left(x\right)$ .

Lời giải:

Đáp án đúng là: A

Theo lí thuyết ta có, hàm số y = f(x) liên tục tại x = a khi và chỉ khi $\underset{x\to a}{\lim }f\left(x\right)=f\left(a\right)$ .

Bài 27 trang 81 SBT Toán 11 Tập 1: Cho đồ thị hàm số y = f(x) trong Hình 7. Phát biểu nào sau đây là sai?

A. Hàm số y = f(x) không liên tục tại x = 1.

B. Hàm số y = f(x) không liên tục tại x = 3.

C. Hàm số y = f(x) không liên tục tại x = 5.

D. Hàm số y = f(x) không liên tục tại x = 0. 

Lời giải:

Đáp án đúng là: D

Quan sát Hình 7, ta thấy

- Hàm số y = f(x) không liên tục tại x = 1, x = 3 và x = 5 vì không tồn tại giá trị của f(x) khi x = 1, x = 3 và x = 5.

- Hàm số  y = f(x) liên tục tại x = 0 nên đáp án D sai.

Bài 28 trang 81 SBT Toán 11 Tập 1: Quan sát đồ thị hàm số trong Hình 8 và cho biết hàm số đó có liên tục:

a) Tại x = $\frac{5}{3}$  hay không. 

b) Trên khoảng (− ∞; 0) hay không.

Lời giải:

Dựa vào đồ thị, ta có:

a) Hàm số không liên tục tại x = $\frac{5}{3}$ vì giá trị hàm số không xác định tại x = $\frac{5}{3}$.

b) Hàm số liên tục trên khoảng(− ∞; 0).

Bài 29 trang 81 SBT Toán 11 Tập 1: Xét tính liên tục của các hàm số sau:

a) $f\left(x\right)=-x^2+\cos x$ ;

b) $g\left(x\right)=3x^3+2-\frac{3}{x+2}$ ;

c) $h\left(x\right)=\frac{2x+5}{x+2}+\frac{3x-1}{2x-4}$ .

Lời giải:

a) Vì hai hàm số y = – x² và y = cos x đều liên tục trên tập xác định của chúng là ℝ nên hàm số $f\left(x\right)=-x^2+\cos x$ liên tục trên ℝ.

b) Vì hàm số y = 3x³ + 2 liên tục trên ℝ, hàm số $y=\frac{3}{x+2}$  liên tục trên hai khoảng (−∞; – 2) và (– 2; +∞) nên hàm số $g\left(x\right)=3x^3+2-\frac{3}{x+2}$liên tục trên hai khoảng (–∞; – 2) và (− 2; +∞).

c) Vì hàm số $y=\frac{2x+5}{x+2}$  liên tục trên hai khoảng (–∞; – 2) và (− 2; +∞), hàm số $y=\frac{3x-1}{2x-4}$  liên tục trên hai khoảng (−∞; 2) và (2; +∞) nên hàm số $h\left(x\right)=\frac{2x+5}{x+2}+\frac{3x-1}{2x-4}$ liên tục trên các khoảng (–∞; – 2), (–2; 2), (2; +∞).

Bài 30 trang 81 SBT Toán 11 Tập 1: Cho hàm số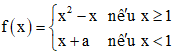 

a) Với a = 2, xét tính liên tục của hàm số tại x = 1.

b) Tìm a để hàm số liên tục trên ℝ.

Lời giải:

a) Với a = 2, ta có: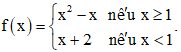 

 $\underset{x\to 1^{+}}{\lim }f\left(x\right)=\underset{x\to 1^{+}}{\lim }\left(x^2-x\right)=0$ và $\underset{x\to 1^{-}}{\lim }f\left(x\right)=\underset{x\to 1^{-}}{\lim }\left(x+2\right)=3$.

Do đó, $\underset{x\to 1^{+}}{\lim }f\left(x\right)\ne \underset{x\to 1^{-}}{\lim }f\left(x\right)$. Suy ra không tồn tại $\underset{x\to 1}{\lim }f\left(x\right)$.

Vậy hàm số đã cho không liên tục tại x = 1 khi a = 2.

b) Với x < 1 thì f(x) = x + a liên tục trên (−∞; 1).

Với x > 1 thì f(x) = x² – x liên tục trên (1; +∞).

Để hàm số liên tục trên ℝ thì hàm số phải liên tục tại x = 1.

Khi đó $\underset{x\to 1^{+}}{\lim }f\left(x\right)=\underset{x\to 1^{-}}{\lim }f\left(x\right)=\underset{x\to 1}{\lim }f\left(x\right)=f\left(1\right)=0$.

Như vậy, $\underset{x\to 1^{-}}{\lim }f\left(x\right)=\underset{x\to 1^{-}}{\lim }\left(x+a\right)=1+a=0\Rightarrow a=-1$.

Vậy hàm số đã cho liên tục trên ℝ khi a = −1.

Bài 31 trang 81 SBT Toán 11 Tập 1: Theo quyết định số 2019/QĐ-BĐVN ngày 01/11/2018 của Tổng công ty Bưu điện Việt Nam, giá cước dịch vụ Bưu chính phổ cập đối với dịch vụ thư cơ bản và bưu thiếp trong nước có khối lượng đến 250 g như trong bảng sau:

a) Hãy biểu diễn số tiền phải trả khi sử dụng dịch vụ thư cơ bản và bưu thiếp theo khối lượng của thư cơ bản và bưu thiếp.

b) Hàm số trên có liên tục trên tập xác định hay không?

Lời giải:

a) Từ giả thiết, ta có hàm số biểu diễn số tiền phải trả khi sử dụng dịch vụ thư cơ bản và bưu thiếp theo khối lượng của thư cơ bản và bưu thiếp là:

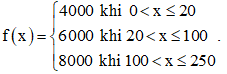
b) Tập xác định của hàm số trên là (0; 250].

Ta có: $\underset{x\to {20}^{-}}{\lim }f\left(x\right)=4000$ , $\underset{x\to {20}^{+}}{\lim }f\left(x\right)=6000$ .

Suy ra không tồn tại $\underset{x\to 20}{\lim }f\left(x\right)$ .

Do đó, hàm số không liên tục tại x = 20.

Vậy hàm số không liên tục trên tập xác định (0; 250].

Xem thêm các bài SBT Toán 11 Cánh Diều hay, chi tiết khác:

Bài 2: Giới hạn của hàm số

Bài tập cuối chương 3

Bài 1: Đường thẳng và mặt phằng trong không gian

Bài 2: Hai đường thẳng song song trong không gian

Bài 3: Đường thẳng và mặt phẳng song song