Toptailieu.vn xin giới thiệu 30 câu trắc nghiệm Hai mặt phẳng song song (có đáp án) chọn lọc, hay nhất giúp học sinh lớp 10 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán. Tài liệu gồm có các nội dung chính sau:

Mời các bạn đón xem:

30 câu trắc nghiệm Hai mặt phẳng song song (có đáp án) chọn lọc

Câu 1: Cho hai đường thẳng chéo nhau a và b. (P) chứa a và song song với b, Q chưa b và song song với a. Phát biểu nào sau đây là đúng?

A.  (P) và (Q) cắt nhau

B.   (P) và (Q) song song với nhau

C.   (P) và (Q) trùng nhau

D.  (P) và (Q) cắt nhau hoặc song song với nhau.

Lời giải:

Đáp án: B

Câu 2: Trong các mệnh đề sau, mệnh đề nào sai.

A.   Hai mặt phẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau.

B.   Nếu hai mặt phẳng phân biệt lần lượt đi qua hai đường thẳng song song thì cắt mặt phẳng còn lại.

C.  Nếu một đường thẳng cắt một trong hai mặt phẳng song song thì cắt mặt phẳng còn lại.

D.  Cho mặt phẳng (P) và ba điểm không thẳng hàng A, B, C nằm ngoài (P) lúc đó, nếu 3 đường thẳng AB, BC, CA đều cắt mặt phẳng (P) thì ba giao điểm đó thẳnghàng.                                                            

Lời giải:

Đáp án: B

   B sai vì hai mặt phẳng đó có thể cắt nhau. Đáp án B.

Câu 3: Cho hình bình hành ABCD. Qua các đỉnh A, B, C, D ta dựng các nửa đường thẳng song song với nhau và nằm về một phía đối với mặt phẳng (ABCD). Một mặt phẳng (P) cắt bốn đường thẳng nói trên tại A’, B’, C’, D’. Hỏi A’B’C’D’ là hìnhgì?

A.  Hình thoi

B.   Hình thang có đúng một cặp cạnh song song

C.   Hình chữ nhật   

D. Hình bình hành

Lời giải:

Đáp án: D

   Vận dụng kết quả giao tuyến của một mặt phẳng với hai mặt phẳng song song là hai đường thẳng song song, ta có tứ giác A’B’C’D’ là hình bình hành. Đáp án D.

Câu 4: Cho hình lăng trụ ABC.A’B’C’. gọi I, J, K lần lượt là trọng tâm của các tam giác ABC, ACC’, A’B’C’. mặt phẳng nào sau đây song song với (IJK)?

 A. (ABC)     

B. (A’BC’)

C. (BB’C’)     

D. (AA’C)

Lời giải:

Đáp án: C

   Gọi M là trung điểm của AC, ta có:

Gọi M là giao điểm của AC và BD, N là giao điểm AC’ và B’D’. ta có MN là đường trung bình của tam giác ACC’ và cũng là đường trung bình hình thang BB’’D’’D nên CC’ = 2MN = BB’ + DD’ = 6.

Câu 8: Khẳng định nào sau đây là đúng?

A.  nếu mặt phẳng (P) chứa hai đường thẳng cùng song song với mặt phẳng (Q) thì (P) // (Q).

B.  nếu hai đường thẳng cùng nằm trong một mặt phẳng lần lượt song song với hai đường thẳng của một mặt phẳng khác thì hai mặt phẳng đó song song.

C.  hai mặt phẳng cùng song song với mặt phẳng thứ ba thì song song với nhau

D.  cho hai mặt phẳng (P) , (Q) song song. Khi đó nếu đường thẳng a không nằm trong mặt phẳng (Q) và a song song với (P) thì a song song với (Q)

Lời giải:

Đáp án: D

Câu 9: Trong các mệnh đề sau, những mệnh đề nào đúng?

(1)   hai mặt phẳng phân biệt cùng song song với một đường thẳng thì song song với nhau.

(2)   hai mặt phẳng phân biệt không song song thì cắt nhau.

(3)   hai mặt phẳng cùng song song với một mặt phảng thứ ba thì song song với nhau.

   Một đường thẳng cắt một trong hai mặt phẳng song song thì cắt mặt phẳng còn lại.

A.(1), (2)     

B. (1), (2), (3)   

C. (2), (4)     

D. (1), (2), (3), (4)

Lời giải:

Đáp án: C

Câu 10: Cho hai mặt phẳng phân biệt (P) và (Q)

(1) nếu hai mặt phẳng (P) và (Q) song song với nhay thì mọi đường thẳng nằm trên (P) đều song song với mọi đường thẳng nằm trên (Q).

(2) nếu mọi đường thẳng nằm trong mặt phẳng (P) đều song song với (Q) thì (P) song song với (Q).

   Trong hai phát biểu trên.

A.  chỉ có một phát biểu đúng.

B.   chỉ có phát biểu (2) đúng.

C.   cả hai phát biểu đều đúng.

 D. cả hai phát biểu đều sai.

Lời giải:

Đáp án: B

Câu 11: Cho mặt phẳng (R) cắt hai mặt phẳng song song (P) và (Q) theo hai giao tuyến a và b. Khi đó.

A.  a và b có một điểm chúng duy nhất

B.   a và b không có điểm chung nào

C.   a và b trùng nhau

D.  a và b song song hoặc trùng nhau

Lời giải:

Đáp án: B

Câu 12: Khẳng định nào sau đây là sai.

A.  nếu a // b, a ⊄ (P), b ⊂ (P) thì a // (P)

B.   nếu ⊂ (P), (P) // (Q) thì a// (Q)

C.   nếu 3 đường thẳng chắn trên hai cát tuyến những đoạn thẳng tương ứng tỉ lệ thì ba đường thẳng đó song song với nhau.

D.  a // b, a // (P). b ⊄ (P) ⇒ b//(P)

Lời giải:

Đáp án: C

Câu 13: Cho hai hình bình hành ABCD và ABEF có tâm lần lượt là O, O’ và không cùng nằm trong một mặt phẳng. gọi M là trung điểm của AB.

(I) (ADF) // (BCE)      (II) (MOO’) // (ADF)

   (III) (MOO’) // (BCE)      (IV) (AEC) // (BDF)

   Khẳng định nào sau đây là đúng

A.chỉ có (1) đúng     

B. chỉ có (1) và (2) đúng   

C. (I), (II), (III) đúng     

D. chỉ có (1) và (IV) đúng

Lời giải:

Đáp án: C

Câu 14: Cho tứ diện đều S.ABC. Gọi I là trung điểm của AB, M là một điểm lưu động trên đoạn AI. Qua M vẽ mặt phẳng () //(SIC). Khi đó thiết diện của mặt phẳng () và tứ diện S.ABC là:

A. tam giác cân tại M     

B. tam giác đều

C. hình bình hành     

D. hình thoi

Lời giải:

Đáp án: A

Câu 15: Cho hình bình hành ABCD. Gọi Bx, Cy, Dz là các đường thẳng đi qua B, C, D và song song với nhau. Mặt phẳng () đi qua A và cắt Bx, Cy, Dz lần lượt tại A’, C’, D’ với BB’ = 2, DD’ = 4. Khi đó CC’ bằng:

A. 3     

B. 4     

C. 5     

D. 6

Lời giải:

Đáp án: D

Câu 16: Cho hình lăng trụ ABC.A’B’C’. gọi I. J. K lần lượt là trọng tâm của các tam giác ABC, ACC’, A’B’C’. Mặt phẳng nào sau đây song song với (IJK)

 A. (AA’B’)     

B. (AA’C’)   

C. (A’B’C’)     

D. (BB’C’)

Lời giải:

Đáp án: D

Câu 17: Cho hai đường thẳng song song a và b. Có bao nhiêu mặt phẳng chứa a  và song song với b ?

A.  0

B.   1

C.  2

D.  vô số.

Lời giải:

Đáp án: D

Giải thích:

Theo tính chất: Có vô số mặt phẳng chứa đường thẳng này và song song với đường thẳng kia. Câu 18: Trong không gian có bao nhiêu vị trí tương đối giữa đường thẳng và mặt phẳng?

A. 1.

B.   2.

C.  3.

D.  4.

Lời giải:

Đáp án: C

Giải thích:

Vị trí tương đối của đường thẳng và mặt phẳng là

•  Đường thẳng nằm trong mặt phẳng.

•  Đường thẳng song song với mặt phẳng.

•  Đường thẳng cắt mặt phẳng.

Câu 19: Cho hai đường thẳng a và b chéo nhau. Có bao nhiêu mặt phẳng chứa a và song song với b?

A. 0.

B.   1.

C.  2.

D.  Vô số.

Lời giải:

Đáp án: B

Giải thích:

Theo định lý 3. Cho hai đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia. 

Câu 20: Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Giao tuyến của hai mặt phẳng (SAD) và (SBC) là đường thẳng song song với đường thẳng nào sau đây?

A.  AC      

B.   BD

C.  AD      

D.  SC

Lời giải:

Đáp án: C

Câu 21: Cho hình chóp S.ABCD, M, N, P, Q lần lượt là trọng tâm các tam giác SAB, SBC, SCD, SDA. Khẳng định nào sau đây là đúng?

A. MNPQ là hình bình hành.

B.   MNPQ là hình thoi.

C.  MNPQ là hình thang chỉ có một cặp cạnh đối song song.

D.  MNPQ là tứ giác không có cặp cạnh nào song song.

Lời giải:

Đáp án: A

Câu 22: Cho tứ diện đều ABCD cạnh a. I, J lần lượt là trung điểm của AC và BC. Gọi K là giao điểm trên cạnh BD với KB = 2KD. Thiết diện của tứ diện với mặt phẳng (IJK) là hình gì?

A.  thiết diện là hình thang cân.

B.   hình bình hành.

C.  tam giác.

D.  tứ giác không có cặp cạnh nào song song.

Lời giải:

Đáp án: A

Giải thích:

 I, J lần lượt là trung điểm của AC và BC nên IJ // AB. Do đó giao tuyến của (IJK) với (ABD) là đường thẳng đi qua K và song song với AB cắt AD tại H. Vậy IJ // KH // AB. Ta có ∆BJK = ∆AIH  JK = IH. Hơn nữa KH ≠ IJ.

   Vậy thiết diện là hình thang cân IJKH.

Câu 23: Cho tứ diện ABCD, G là trọng tâm của tam giác ABD, M là điểm trên cạnh BC sao cho MB = 2MC. Khẳng định nào sau đây là đúng?

A.  MG // (ACD)      

B.   MG // (ABC)

C.  MG // AB      

D.  MG cắt AC

Lời giải:

Đáp án: A Giải thích:

(hình 1) G là trọng tâm của tam giác ABD nên:

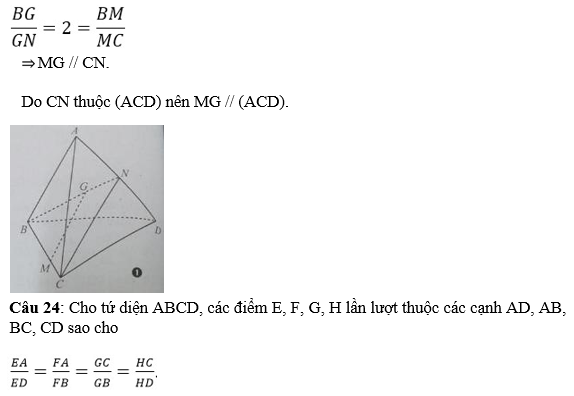
Khẳng định nào sau đây là đúng?

A.  EFGH là hình bình hành.

B.   EFGH có đúng một cặp cạnh song song.

C.  EFGH là tứ giác không có cặt cạnh nào song song.

D.  EFGH là hình chữ nhật.

Lời giải:

Đáp án: A

Giải thích:

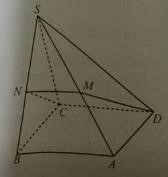
Câu 25: Cho hình chóp S.ABCD, đáy ABCD là hình bình hành. Gọi M là trung điểm của SA. Thiết diện của mặt phẳng (MCD) với hình chóp S.ABCD là hình gì?

A.  tam giác      

B.   hình bình hành

C.  hình thang      

D.  hình thoi

Lời giải:

Đáp án: C

Giải thích: 

Vì CD  (MCD), CD // AB, AB  (SAB) nên giao tuyến của (MCD) và (SAB) là đường thẳng qua M và song song với AB, cắt SB tại N là trung điểm của SB. Vậy MN // CD. Hơn nữa MN ≠ CD. Vậy thiết diện là hình thang CNMD.

Câu 26: Cho hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng, có tâm lần lượt là O và O’. Chọn khẳng định đúng trong các khẳng định sau:

A.  OO’ // (ABCD)      

B.   OO’ // (ABEF)

C.  OO’ // (BDF)      

D.  OO’ / /(ADF)

Lời giải:

Đáp án: D

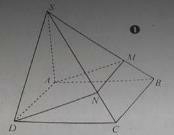
Câu 27: Hình chóp S.ABCD có đáy là hình bình hành ABCD. Giả sử M thuộc đoạn thẳng SB. Mặt phẳng (ADM) cắt hình chóp S.ABCD theo thiết diện là hình:

A. tam giác      

B.   hình thang

C.  hình bình hành      

D.  hình thoi

Lời giải:

Đáp án: D Giải thích:

(hình 1) Do AD//BC, M thuộc (SBC) nên giao tuyến của (ADM) với (SBC) là đường thẳng qua M và song song với BC, đường thẳng này cắt SC tại N.

Ta có MN//AD. Vậy thiết diện là hình thang AMND.

Câu 28: Cho đường thẳng d song song với mặt phẳng (), mặt phẳng (β) chứa d và cắt () theo giao tuyến d’. Khẳng định nào sau đây là đúng ?

A.  d’ // d hoặc d’ ≡ d      

B.   d’ // d

C.  d’ ≡ d      

D.  d’ và d chéo nhau

Lời giải:

Đáp án: B

Câu 29: Cho hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) sẽ:

A.  song song với hai đường thẳng đó

B.   song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.

C.  trùng với một trong hai đường thẳng đó

D.  cắt một trong hai đường thẳng đó

Lời giải:

Đáp án: B

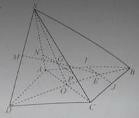
Câu 30: Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi I, J lần lượt là trung điểm của AB và CB. M là điểm thuộc cạnh SD. Khẳng định nào sau đây là đúng? A. Giao tuyến của hai mặt phẳng (SAC) và (MIJ) và đường thẳng AC cắt nhau.

B.   Giao tuyến của hai mặt phẳng (SAC) và (MIJ) và đường thẳng AC chéo nhau.

C.  Giao tuyến của hai mặt phẳng (SAC) và (MIJ) và đường thẳng BD cắt nhau.

D.  Giao tuyến của hai mặt phẳng (SAC) và (MIJ) và đường thẳng AC song song với nhau.

Lời giải:

Đáp án: D

Giải thích: Trong mặt phẳng (ABCD) ta có AC cắt BD tại O, IJ cắt BD tại E. trong mặt phẳng (SBD), ME cắt SO tại G.

Ta có G thuộc (MIJ). (MIJ) chứa IJ // AC nên giao tuyến của (MIJ) với (SAC) là đường thẳng qua G và song song với AC.