Toptailieu.vn xin giới thiệu sơ lược Lý thuyết Hai mặt phẳng song song (Lý thuyết + 35 bài tập có lời giải) Toán 11 chọn lọc, hay nhất giúp học sinh lớp 11 ôn luyện để nắm chắc kiến thức cơ bản và đạt kết quả cao trong các bài thi môn Toán.

Mời các bạn đón xem:

Hai mặt phẳng song song (Lý thuyết + 35 bài tập có lời giải)

I. Lý thuyết Hai mặt phẳng song song

1. Vị trí tương đối của hai mặt phẳng phân biệt

    Cho 2 mặt phẳng (P) và (Q). Căn cứ vào số đường thẳng chung của 2 mặt phẳng ta có ba trường hợp sau:

a. Hai mặt phẳng (P) và (Q) không có đường thẳng chung, tức là:

  (P) ⋂ (Q) = ∅ ⇔ (P) // (Q).

b. Hai mặt phẳng (P) và (Q) chỉ có một đường thẳng chung, tức là:

        (P) ⋂ (Q) = a ⇔ (P) cắt (Q).

c. Hai mặt phẳng (P) và (Q) có 2 đường thẳng chung phân biệt, tức là:

        (P) ⋂ (Q) = {a, b} ⇔ (P) ≡ (Q).

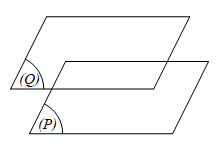
        (P) ⋂ (Q) = ∅ ⇔ (P) // (Q).

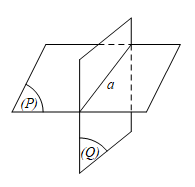
        (P) ⋂ (Q) = a ⇔ (P) cắt (Q).

(P) ⋂ (Q) = {a, b} ⇔ (P) ≡ (Q).

2. Điều kiện để hai mặt phẳng song song

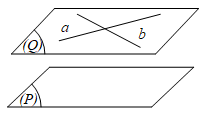
Định lí 1: Nếu mặt phẳng (P) chứa hai đường thẳng a, b cắt nhau và cùng song song với mặt phẳng (Q) thì (P) song song (Q).

Tức là: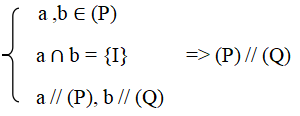 

3. Tính chất

Tính chất 1: Qua một điểm nằm ngoài một mặt phẳng, có một và chỉ một mặt phẳng song song với mặt phẳng đó.

Tức là: O ∉ (P) ⇒ ∃! (Q):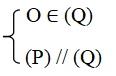 

Cách dựng:

    + Trong (P) dựng a, b cắt nhau.

    + Qua O dựng a₁ // a, b₁ // b.

    + Mặt phẳng (a₁, b₁) là mặt phẳng qua O và song song với (P).

Hệ quả 1: Nếu đường thẳng a song song với mặt phẳng (Q) thì qua a có một và chỉ một mặt phẳng (P) song song với (Q).

Hệ quả 2: Hai mặt phẳng phân biệt cùng song song với một mặt phẳng thứ ba thì song song với nhau.

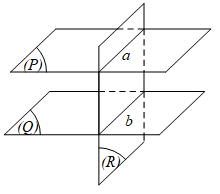
Tính chất 2: Nếu hai mặt phẳng (P) và (Q) song song thì mặt phẳng (R) đã cắt (P) thì phải cắt (Q) và các giao tuyến của chúng song song.

Tức là: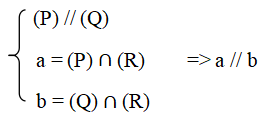 

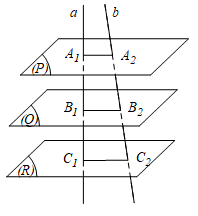
Định lí Ta – lét trong không gian: Ba mặt phẳng đôi một song song chắn trên hai cát tuyến bất kì các đoạn thẳng tương ứng tỷ lệ.

Tức là:

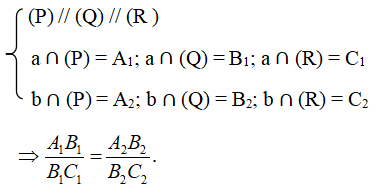
4. Hình lăng trụ và hình hộp

Định nghĩa hình lăng trụ: Hình lăng trụ là một hình đa diện có hai mặt nằm trong hai mặt phẳng song song gọi là hai đáy và tất cả các cạnh không thuộc hai cạnh đáy đều song song với nhau.

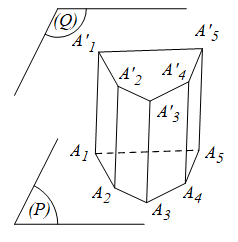
Trong đó:

    + Các mặt khác với hai đáy gọi là các mặt bên của hình lăng trụ.

    + Cạnh chung của hai mặt bên gọi là cạnh bên của hình lăng trụ.

    + Tùy theo đa giác đáy, ta có hình lăng trụ tam giác, lăng trụ tứ giác …

Từ định nghĩa của hình lăng trụ, ta lần lượt suy ra các tính chất sau:

a. Các cạnh bên song song và bằng nhau.

b. Các mặt bên và các mặt chéo là những hình bình hành.

c. Hai đáy là hai đa giác có các cạnh tương ứng song song và bằng nhau.

Định nghĩa hình hộp: Hình lăng trụ có đáy là hình bình hành gọi là hình hộp.

    a. Hình hộp có tất cả các mặt bên và các mặt đáy đều là hình chữ nhật gọi là hình hộp chữ nhật.

    b. Hình hộp có tất cả các mặt bên và các mặt đáy đều là hình vuông gọi là hình lập phương.

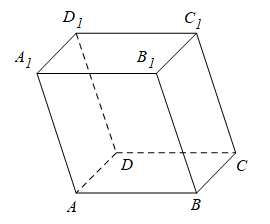
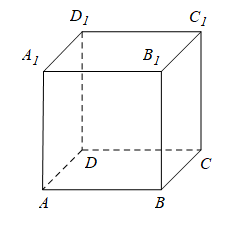
Chú ý: Các đường chéo của hình hộp cắt nhau tại trung điểm mỗi đường.

5. Hình chóp cụt

Định nghĩa: Cho hình chóp S.A₁A₂…A_n. Một mặt phẳng (P) song song với mặt phẳng chứa đa giác đáy cắt các cạnh SA₁, SA₂,…, SA_n theo thứ tự tại A'₁, A'₂,…, A'_n. Hình tạo bởi thiết diện A'₁A'₂…A'_n và đáy A₁A₂…A_n của hình chóp cùng với các mặt bên A₁A₂A'₂A'₁, A₂A₃A'₃A'₂,…, A_nA₁A'₁A'_n gọi là một hình chóp cụt.

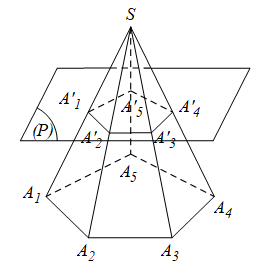
Trong đó:

    + Đáy của hình chóp gọi là đáy lớn của hình chóp cụt, còn thiết diện gọi là đáy nhỏ của hình chóp cụt.

    + Các mặt còn lại gọi là các mặt bên của hình chóp cụt.

    + Cạnh chung của hai mặt bên kề nhau như A₁A'₁, A₂A'₂,…, A_nA'_n gọi là cạnh bên của hình chóp cụt.

Tùy theo đáy là tam giác, tứ giác, ngũ giác,… ta có hình chóp cụt tam giác, hình chóp cụt tứ giác, hình chụp cụt ngũ giác,…

Tính chất: Với hình chóp cụt, ta có các tính chất sau:

    1. Hai đáy của hình chóp cụt là hai đa giác đồng dạng.

    2. Các mặt bên của hình chóp cụt là các hình thang.

    3. Các cạnh bên của hình chóp cụt đồng quy tại một điểm.

II. Bài tập Hai mặt phẳng song song

Câu 1: Một mặt phẳng cắt hai mặt đối diện của hình hộp theo hai giao tuyến là a và b.  Hãy Chọn Câu đúng:

A. a và b song song.

B. a và b chéo nhau.

C. a và b trùng nhau.

D. a và b cắt nhau.

Đáp án: A

Câu 2: Chọn Câu đúng :

A. Hai đường thẳng a và b không cùng nằm trong mặt phẳng (P) nên chúng chéo nhau.

B. Hai đường thẳng không song song thì chéo nhau.

C. Hai đường thẳng phân biệt lần lượt nằm trên hai mặt phẳng khác nhau thì chéo nhau.

D. Hai đường thẳng không song song và lần lượt nằm trên hai mặt phẳng song song thì chéo nhau.

Đáp án: D

Câu 3: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và M, N lần lượt là trung điểm của AB, CD. Xác định thiết diện của hình chóp cắt bởi $\left(\alpha \right)$ đi qua MN và song song với mặt phẳng (SAD).Thiết diện là hình gì?

A. Tam giác

B. Hình thang

C. Hình bình hành

D. Tứ giác

Đáp án: B

Câu 4: Chọn Câu đúng :

A. Hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì chúng song song.

B. Hai đường thẳng cùng song song với một mặt phẳng thì song song với nhau.

C. Hai mặt phẳng không cắt nhau thì song song.

D. Hai mặt phẳng không song song thì trùng nhau.

Đáp án: A

Câu 5: Hãy Chọn Câu sai :

A. Nếu hai mặt phẳng song song thì mọi đường thẳng nằm trên mặt phẳng này đều song song với mặt phẳng kia.

B. Nếu mặt phẳng (P) chứa hai đường thẳng cùng song song với mặt phẳng (Q) thì (P) và (Q) song song với nhau.

C. Nếu hai mặt phẳng (P) và (Q) song song nhau thì mặt phẳng (R) đã cắt (P) đều phải cắt (Q) và các giao tuyến của chúng song song nhau.

D. Nếu một đường thẳng cắt một trong hai mặt phẳng song song thì sẽ cắt mặt phẳng còn lại.

Đáp án: B

Câu 6: Cho một đường thẳng a song song với mặt phẳng (P). Có bao nhiêu mặt phẳng chứa a và song song với (P)?

A. 0.

B. 1.

C. 2.

D. vô số.

Đáp án: B

Câu 7: Hãy Chọn Câu đúng :

A. Nếu hai mặt phẳng song song thì mọi đường thẳng nằm trên mặt phẳng này đều song song với mọi đường thẳng nằm trên mặt phẳng kia.

B. Nếu hai mặt phẳng (P) và (Q) lần lượt chứa hai đường thẳng song song thì song song với nhau.

C. Hai mặt phẳng cùng song song với một đường thẳng thì song song với nhau.

D. Hai mặt phẳng phân biệt không song song thì cắt nhau.

Đáp án: D

Câu 8: Cho một điểm A nằm ngoài mp(P). Qua A vẽ được bao nhiêu đường thẳng song song với (P)?

A. 1.

B. 2.

C. 3.

D. vô số.

Đáp án: D

Câu 9: Cho đường thẳng a nằm trên mp$\left(\alpha \right)$ và đường thẳng b nằm trên mp$\left(\beta \right)$. Biết $\left(\alpha \right)\text{//}\left(\beta \right)$.

Tìm câu sai:

A. $a\text{//}\left(\beta \right)$

B. $b\text{//}\left(\alpha \right)$

C. $a\text{//}b$

D. Nếu có một mp $\left(\gamma \right)$ chứa a và b thì $a\text{//}b$

Đáp án: C

Câu 10: Giả thiết nào sau đây là điều kiện đủ để kết luận đường thẳng a song song với mp$\left(\alpha \right)$?

A. $a\parallel b$ và $b\parallel \left(\alpha \right)$.

B. $a\parallel b$ và $b\subset \left(\alpha \right)$.

C. $a\parallel mp\left(\beta \right)$ và $\left(\beta \right)\parallel \left(\alpha \right)$.

D. $a\cap \left(\alpha \right)=\varnothing$.

Đáp án: D

Câu 11: Cho đường thẳng a nằm trong mặt phẳng $\left(\alpha \right)$ và đường thẳng b nằm trong mặt phẳng $\left(\beta \right)$. Mệnh đề nào sau đây SAI?

A. $\left(\alpha \right)\text{//}\left(\beta \right)\Rightarrow a\text{//}b$.

B. $\left(\alpha \right)\text{//}\left(\beta \right)\Rightarrow a\text{//}\left(\beta \right)$.

C. $\left(\alpha \right)\text{//}\left(\beta \right)\Rightarrow b\text{//}\left(\alpha \right)$.

D. a và b hoặc song song hoặc chéo nhau.

Đáp án: A

Câu 12: Cho hình hộp $ABCD.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$. Khẳng định nào sau đây SAI?

A. $A{B}^{\text{'}}{C}^{\text{'}}D$ và $A^{\text{'}}BC{D}^{\text{'}}$ là hai hình bình hành có chung một đường trung bình.

B. $B{D}^{\text{'}}$ và $B^{\text{'}}{C}^{\text{'}}$ chéo nhau.

C. $A^{\text{'}}C$ và $D{D}^{\text{'}}$ chéo nhau.

D. $D{C}^{\text{'}}$ và $A{B}^{\text{'}}$ chéo nhau.

Đáp án: D

Câu 13: Cho hình hộp $ABCD.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$. Người ta định nghĩa ‘Mặt chéo của hình hộp là mặt tạo bởi hai đường chéo của hình hộp đó’. Hỏi hình hộp $ABCD.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$ có mấy mặt chéo ?

A. 4.

B. 6.

C. 8.

D. 10.

Đáp án: B

Câu 14: Cho hình hộp $ABCD.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$. Mp$\left(\alpha \right)$ qua AB cắt hình hộp theo thiết diện là hình gì?

A. Hình bình hành.

B. Hình thoi.

C. Hình vuông.

D. Hình chữ nhật.

Đáp án: A

Câu 15: Cho hình hộp $ABCD.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$. Gọi O và $O\text{'}$ lần lượt là tâm của $AB{B}^{\text{'}}{A}^{\text{'}}$ và $DC{C}^{\text{'}}{D}^{\text{'}}$. Khẳng định nào sau đây sai ?

A. $\overrightarrow{O{O}^{\text{'}}}=\overrightarrow{AD}$.

B. $O{O}^{\text{'}}\text{//}\left(AD{D}^{\text{'}}{A}^{\text{'}}\right)$.

C. $O{O}^{\text{'}}$ và $B{B}^{\text{'}}$ cùng ở trong một mặt phẳng.

D. $O{O}^{\text{'}}$ là đường trung bình của hình bình hành $AD{C}^{\text{'}}{B}^{\text{'}}$.

Đáp án: C

Câu 16: Cho hình hộp $ABCD.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$. Mặt phẳng $\left(A{B}^{\text{'}}{D}^{\text{'}}\right)$ song song với mặt phẳng nào trong các mặt phẳng sau đây?

A. $\left(BC{A}^{\text{'}}\right)$.

B. $\left(B{C}^{\text{'}}D\right)$.

C. $\left(A^{\text{'}}{C}^{\text{'}}C\right)$.

D. $\left(BD{A}^{\text{'}}\right)$.

Đáp án: B

Câu 17: Cho hình hộp $ABCD.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$. Gọi M là trung điểm của AB. Mặt phẳng $\left(M{A}^{\text{'}}{C}^{\text{'}}\right)$ cắt hình hộp $ABCD.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$ theo thiết diện là hình gì?

A. Hình tam giác.

B. Hình ngũ giác.

C. Hình lục giác.

D. Hình thang.

Đáp án: D

Câu 18: Cho hình bình hành ABCD. Vẽ các tia $Ax,By,Cz,Dt$ song song, cùng hướng nhau và không nằm trong mp(ABCD). Mp $\left(\alpha \right)$ cắt $Ax,By,Cz,Dt$ lần lượt tại $A^{\text{'}},B^{\text{'}},C^{\text{'}},D^{\text{'}}$. Khẳng định nào sau đây sai?

A. $A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$ là hình bình hành.

B. mp$\left(A{A}^{\text{'}}{B}^{\text{'}}B\right)\text{// }\left(D{D}^{\text{'}}{C}^{\text{'}}C\right)$.

C. $A{A}^{\text{'}}=C{C}^{\text{'}}$ và $B{B}^{\text{'}}=D{D}^{\text{'}}$

D. $O{O}^{\text{'}}\text{// }A{A}^{\text{'}}$.

(O là tâm hình bình hành ABCD, $O\text{'}$ là giao điểm của $A\text{'}C\text{'}$ và $B\text{'}D\text{'}$).

Đáp án: C

Câu 19: Cho hình hộp $ABCD.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$. Gọi I là trung điểm AB. Mp$\left(I{B}^{\text{'}}{D}^{\text{'}}\right)$ cắt hình hộp theo thiết diện là hình gì?

A. Tam giác.

B. Hình thang.

C. Hình bình hành.

D. Hình chữ nhật.

Đáp án: B

Câu 20: Cho hình lăng trụ $ABC.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}$. Gọi $M,M^{\text{'}}$ lần lượt là trung điểm của BC và $B^{\text{'}}{C}^{\text{'}}$. $G,G^{\text{'}}$ lần lượt là trọng tâm tam giác $ABC$ và $A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}$. Bốn điểm nào sau đây đồng phẳng?

A. $A,G,G^{\text{'}},C^{\text{'}}$.

B. $A,G,M^{\text{'}},B^{\text{'}}$.

C. $A^{\text{'}},G^{\text{'}},M,C$.

D. $A,G^{\text{'}},M^{\text{'}},G$.

Đáp án: D

Câu 21: Cho hình lăng trụ $ABC.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}$. Gọi $M,N$ lần lượt là trung điểm của $B{B}^{\text{'}}$ và $C{C}^{\text{'}}$, $\Delta =mp\left(AMN\right)\cap mp\left(A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}\right)$. Khẳng định nào sau đây đúng ?

A. $\Delta \text{\hspace{0.05em}\hspace{0.05em}// }AB$.

B. $\Delta \text{\hspace{0.05em}\hspace{0.05em}// }AC$.

C. $\Delta \text{\hspace{0.05em}\hspace{0.05em}// }BC$.

D. $\Delta \text{\hspace{0.05em}\hspace{0.05em}//\hspace{0.05em}\hspace{0.05em}}A{A}^{\text{'}}$.

Đáp án: C

Câu 22: Hai đường thẳng a và b nằm trong $\left(\alpha \right)$. Hai đường thẳng $a^{\text{'}}$ và $b\text{'}$ nằm trong mp$\left(\beta \right)$. Mệnh đề nào sau đây đúng?

A. Nếu $a\text{\hspace{0.17em}//\hspace{0.17em}}{a}^{\text{'}}$ và $b\text{\hspace{0.17em}//\hspace{0.17em}}{b}^{\text{'}}$ thì $\left(\alpha \right)\text{//}\left(\beta \right)$.

B. Nếu $\left(\alpha \right)\text{//}\left(\beta \right)$ thì $a\text{\hspace{0.17em}//\hspace{0.17em}}{a}^{\text{'}}$ và $b\text{\hspace{0.17em}//\hspace{0.17em}}{b}^{\text{'}}$.

C. Nếu $a\text{\hspace{0.17em}//\hspace{0.17em}}b$ và $a^{\text{'}}\text{\hspace{0.17em}//\hspace{0.17em}}{b}^{\text{'}}$ thì $\left(\alpha \right)\text{//}\left(\beta \right)$.

D. Nếu a cắt b, a cắt b và $a\text{\hspace{0.17em}//\hspace{0.17em}}{a}^{\text{'}}$ và $b\text{\hspace{0.17em}//\hspace{0.17em}}{b}^{\text{'}}$ thì $\left(\alpha \right)\text{//}\left(\beta \right)$.

Đáp án: D

Câu 23: Cho hai đường thẳng chéo nhau a và b. (P) chứa a và song song với b, Q chưa b và song song với a. Phát biểu nào sau đây là đúng?

A. (P) và (Q) cắt nhau

B. (P) và (Q) song song với nhau

C. (P) và (Q) trùng nhau

D. (P) và (Q) cắt nhau hoặc song song với nhau.

Đáp án: B

Câu 24: Trong các mệnh đề sau, mệnh đề nào sai.

A. Hai mặt phẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau.

B. Nếu hai mặt phẳng phân biệt lần lượt đi qua hai đường thẳng song song thì cắt mặt phẳng còn lại.

D. Hai mặt phẳng phân biệt không song song thì cắt nhau.

C. Nếu một đường thẳng cắt một trong hai mặt phẳng song song thì cắt mặt phẳng còn lại.

D. Cho mặt phẳng (P) và ba điểm không thẳng hàng A, B, C nằm ngoài (P) lúc đó, nếu 3 đường thẳng AB, BC, CA đều cắt mặt phẳng (P) thì ba giao điểm đó thẳng hàng.

Đáp án: D

Câu 25: Cho hình bình hành ABCD. Qua các đỉnh A, B, C, D ta dựng các nửa đường thẳng song song với nhau và nằm về một phía đối với mặt phẳng (ABCD). Một mặt phẳng (P) cắt bốn đường thẳng nói trên tại A’, B’, C’, D’. Hỏi A’B’C’D’ là hình gì?

A. Hình thoi

B. Hình thang có đúng một cặp cạnh song song

C. Hình chữ nhật

D. Hình bình hành

Đáp án: D

Câu 26: Cho hình lăng trụ ABC.A’B’C’. gọi I, J, K lần lượt là trọng tâm của các tam giác ABC, ACC’, A’B’C’. mặt phẳng nào sau đây song song với (IJK)?

A. (ABC)      

B. (A’BC’)

C. (BB’C’)      

D. (AA’C)

Đáp án: C

Câu 27: Cho hai mặt phẳng (∝), (β) cắt nhau và cùng song song với đường thẳng d. Khẳng định nào sau đây là đúng?

A. giao tuyến của (∝), (β) trùng với d

B. giao tuyến của (∝), (β) song song hoặc trùng với d

C. giao tuyến của (∝), (β) song song với d

D. giao tuyến của (∝), (β) cắt d

Đáp án: C

Câu 28: Trong các mệnh đề sau, mệnh đề nào là đúng?

A. nếu (∝) //(β) và d₁ ⊂(∝);d₂ ⊂(β) thì d₁// d₂

B. nếu d₁ // (∝) và d₂ // (β) thì d₁ // d₂

C. nếu (∝) //(β) và d₁ // (∝), thì d₁ // (β) hoặc d₁ ⊂ (β)

D. nếu d₁ // d₂ và d₁⊂(∝),d₂⊂(β) thì (∝) //(β)

Đáp án: C

Câu 29: Cho hai đường thẳng a và b lần lượt nằm trên hai mặt phẳng song song (P) và (Q).

A. a và b là hai đường thẳng song song

B. nếu điểm M không nằm trên (P) và (Q) thì không thể coi đường thẳng nào đi qua M và cắt cả a lẫn b.

C. nếu a và b không song song với nhau, điểm M không nằm trên (P) và (Q), thì luôn có duy nhất một đường thẳng đi qua M cắt cả a và b.

D. cả 3 câu trên đều sai.

Đáp án: C

Câu 30: Khẳng định nào sau đây là đúng?

A. nếu mặt phẳng (P) chứa hai đường thẳng cùng song song với mặt phẳng (Q) thì (P) // (Q).

B. nếu hai đường thẳng cùng nằm trong một mặt phẳng lần lượt song song với hai đường thẳng của một mặt phẳng khác thì hai mặt phẳng đó song song.

C. hai mặt phẳng cùng song song với mặt phẳng thứ ba thì song song với nhau

D. cho hai mặt phẳng (P) , (Q) song song. Khi đó nếu đường thẳng a không nằm trong mặt phẳng (Q) và a song song với (P) thì a song song với (Q)

Đáp án: D

Câu 31: Cho một đường thẳng a song song với mặt phẳng (P). Có bao nhiêu mặt phẳng chứa a và song song với (P)?

A. 0

B. 1

C. 2

D. vô số

Đáp án: B

Câu 32: Cho mặt phẳng (R) cắt hai mặt phẳng song song (P) và (Q) theo hai giao tuyến a và b. Khi đó.

A. a và b có một điểm chúng duy nhất

B. a và b không có điểm chung nào

C. a và b trùng nhau

D. a và b song song hoặc trùng nhau

Đáp án: B

Câu 33: Khẳng định nào sau đây là sai

A. nếu a // b, a ⊄ (P), b ⊂ (P) thì a // (P)

B. nếu ⊂ (P), (P) // (Q) thì a// (Q)

C. nếu 3 đường thẳng chắn trên hai cát tuyến những đoạn thẳng tương ứng tỉ lệ thì ba đường thẳng đó song song với nhau.

D. a // b, a // (P). b ⊄ (P) ⇒ b//(P)

Đáp án: C

Câu 34: Cho hình lăng trụ ABC.A’B’C’. gọi I. J. K lần lượt là trọng tâm của các tam giác ABC, ACC’, A’B’C’. Mặt phẳng nào sau đây song song với (IJK)

A. (AA’B’)      

B. (AA’C’)

C. (A’B’C’)      

D. (BB’C’)

Đáp án: D

Câu 35: Cho hình bình hành ABCD. Gọi Bx, Cy, Dz là các đường thẳng đi qua B, C, D và song song với nhau. Mặt phẳng (∝) đi qua A và cắt Bx, Cy, Dz lần lượt tại A’, C’, D’ với BB’ = 2, DD’ = 4. Khi đó CC’ bằng:

A. 3      

B. 4      

C. 5      

D. 6

Đáp án: D