Toptailieu.vn biên soạn và giới thiệu Lý thuyết Diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác (Chân trời sáng tạo) Toán 7 hay, ngắn gọn và bài tập tự luyện có lời giải chi tiết sẽ giúp học sinh nắm vững nội dung kiến thức từ đó dễ dàng làm các bài tập Toán 7.

Lý thuyết Diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác (Chân trời sáng tạo) Toán 7

A. Lý thuyết

1. Diện tích xung quanh của hình lăng trụ đứng

Diện tích xung quanh của hình lăng trụ đứng bằng chu vi đáy nhân với chiều cao.

S_xq = C_đáy . h

(C_đáy là chu vi đáy, h là chiều cao).

Chú ý: Diện tích toàn phần của hình lăng trụ đứng bằng tổng diện tích xung quanh và diện tích hai đáy.

Ví dụ: Tính diện tích xung quanh và diện tích toàn phần của hình lăng trụ đứng tam giác ABC.DEF sau:

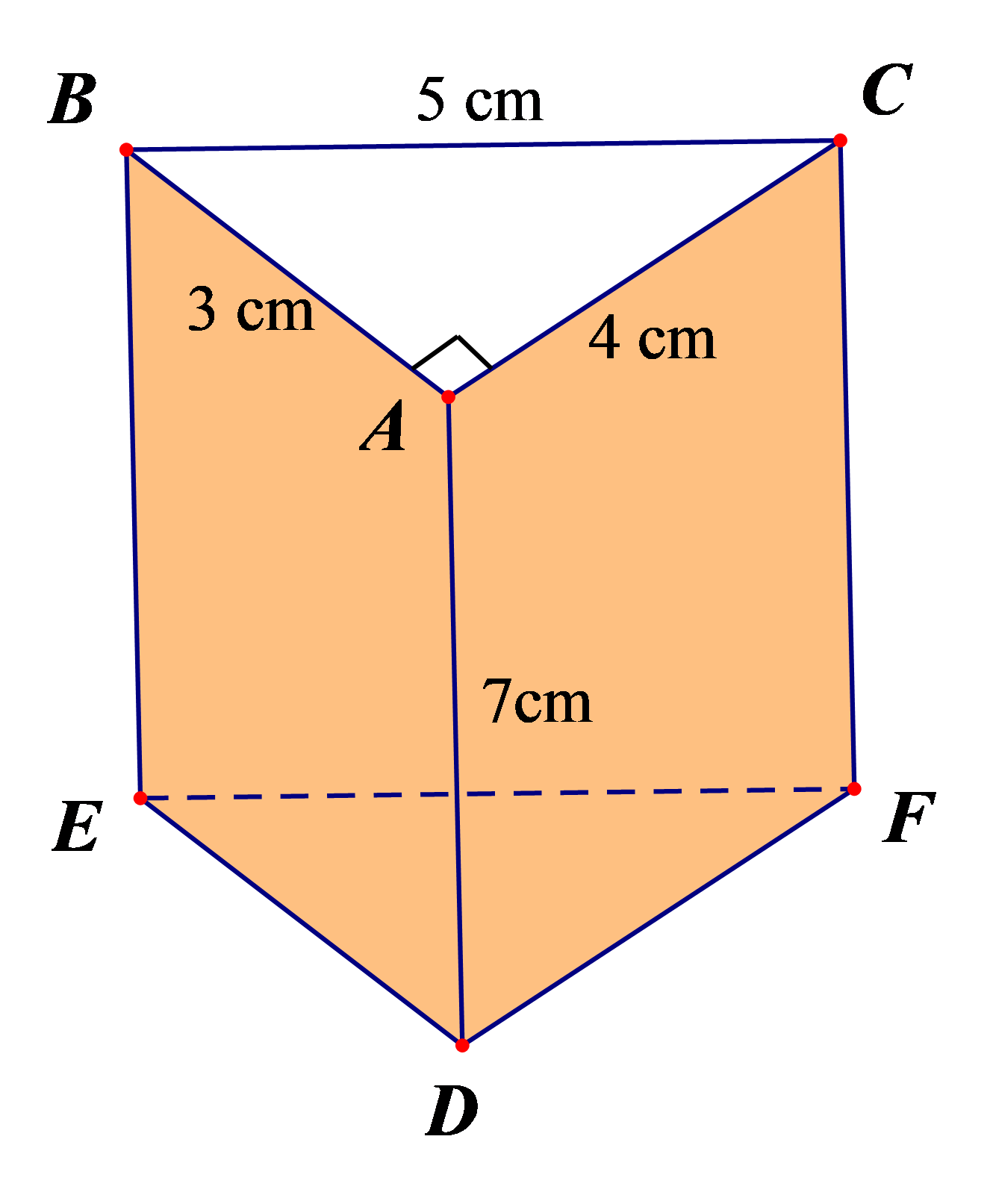
Hướng dẫn giải

Diện tích xung quanh của hình lăng trụ đứng tam giác ABC.DEF là:

S_xq = C_đáy . h = (3 + 4 + 5 ) . 7 = 84 (cm²).

Diện tích một đáy của hình lăng trụ đứng tam giác ABC.DEF là: 

S_đáy =  $\frac{1}{2}.3.4=6$ (cm²)

Diện tích toàn phần của hình lăng trụ đứng tam giác ABC.DEF là:

84 + 2. 6 = 96 (cm²)

Vậy diện tích xung quanh và diện tích toàn phần của hình lăng trụ đứng tam giác ABC.DEF lần lượt là 84 cm² và 96 cm².

2. Thể tích của hình lăng trụ đứng

Thể tích của hình lăng trụ đứng bằng diện tích đáy nhân với chiều cao.

V = S_đáy . h

(S_đáy là diện tích đáy, h là chiều cao).

Ví dụ: Tính thể tích của hình lăng trụ đứng tứ giác có đáy là hình chữ nhật chiều rộng là 3 cm, chiều dài là 4 cm, và chiều cao của lăng trụ là 5,5 cm.

Hướng dẫn giải

Ta có đáy là hình chữ nhật nên diện tích đáy là:

S_đáy = 3 . 4 = 12 (cm²)

Thể tích của hình lăng trụ đứng tứ giác đó là: 

V = S_đáy . h = 12 . 5,5 = 66 (cm³).

Vậy thể tích của hình lăng trụ đứng tứ giác đó là 66 cm³.

3. Diện tích xung quanh và thể tích của một số hình khối trong thực tiễn

Ví dụ: Một tấm lịch để bàn có dạng hình lăng trụ đứng tam giác. Tính diện tích xung quanh của tấm lịch.

Hướng dẫn giải

Diện tích xung quanh của tấm lịch để bàn là:

S_xq = C_đáy . h = (7 + 15 + 15) . 16 = 592 (cm²)

Vậy diện tích xung quanh của tấm lịch là 592 cm².

Ví dụ: Để thi công một con dốc, người ta đúc một khối bê tông hình lăng trụ đứng tam giác có kích thước như hình sau.

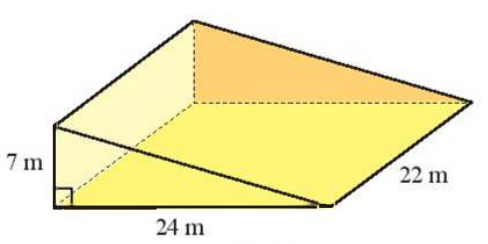
Hãy tính thể tích của khối bê tông.

Hướng dẫn giải

Diện tích đáy của hình lăng trụ đứng tam giác là:

S_đáy = $\frac{1}{2}.7.24$ = 84 (m²).

Thể tích của khối bê tông là:

V = S_đáy . h = 84 . 22 = 1 848 (m³).

Vậy thể tích của khối bê tông là 1 848 m³.

B. Bài tập tự luyện

B.1. Bài tập trắc nghiệm

Câu 1. Cho lăng trụ đứng tam giác ABC.EGH, biết GH = 4 cm. S_BCHG = 36 cm². Chiều cao của lăng trụ là:

A. 32 cm;

B. 9 cm;

C. 40 cm;

D. 10 cm.

Hướng dẫn giải

Đáp án đúng là: B

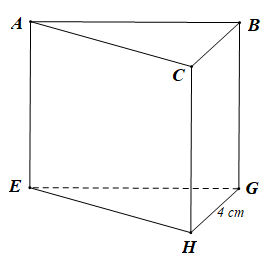
Vì ABC.EGH là lăng trụ đứng tam giác nên mặt bên BCHG là hình chữ nhật.

Do đó S_BCHG = GH. CH = 36 cm²

Mà GH = 4 cm nên CH = S_BCHG : GH = 36 : 4 = 9 (cm).

Chiều cao của hình lăng trụ đứng là độ dài một cạnh bên, mà CH là cạnh bên của hình lăng trụ này.

Vậy chiều cao của lăng trụ đứng ABC.EGH là 9 cm.

Câu 2. Cho hình lăng trụ đứng có đáy là hình vuông, chiều cao bằng 20 cm và diện tích xung quanh bằng 64 cm². Cạnh đáy của hình lăng trụ đứng đó là:

A. 3,2 cm;

B. ± 4 cm;

C. 4 cm;

D. 16 cm.

Hướng dẫn giải

Đáp án đúng là: C

Gọi độ dài cạnh đáy của hình lăng trụ đứng là a (cm) (a > 0).

Diện tích xung quanh của hình lăng trụ đứng đó là:

S_xq = 4 . a²

Do đó 64 = 4 . a²

a² = 16

nên a = 4 hoặc a = –4.

Mà a > 0 nên a = 4 (cm).

Vậy độ dài cạnh đáy của hình lăng trụ đứng đó là 4 cm.

Câu 3. Cho hình lăng trụ đứng tứ giác ABCD.A’B’C’D’ với đáy là hình thoi có độ dài hai đường chéo là 5 cm và 10 cm. Biết thể tích của hình lăng trụ đứng tứ giác là 160 cm³. Chiều cao của hình lăng trụ đứng tứ giác ABCD.A’B’C’D’ là:

A. 32 cm;

B. 8 cm;

C. 6,4 cm;

D. 10 cm.

Hướng dẫn giải

Đáp án đúng là: C

Diện tích đáy (hình thoi) của hình lăng trụ đứng tứ giác ABCD.A’B’C’D’ là:

$\frac{1}{2}$. 5 . 10 = 25 (cm²)

Chiều cao của hình lăng trụ đứng tứ giác ABCD.A’B’C’D’ là:

160 : 25 = 6,4 (cm)

Vậy chiều cao của hình lăng trụ đứng tứ giác ABCD.A’B’C’D’ là 6,4 cm.

B.2. Bài tập tự luận

Bài 1. Một chiếc hộp có dạng hình lăng trụ đứng tam giác với các kích thước như hình vẽ sau.

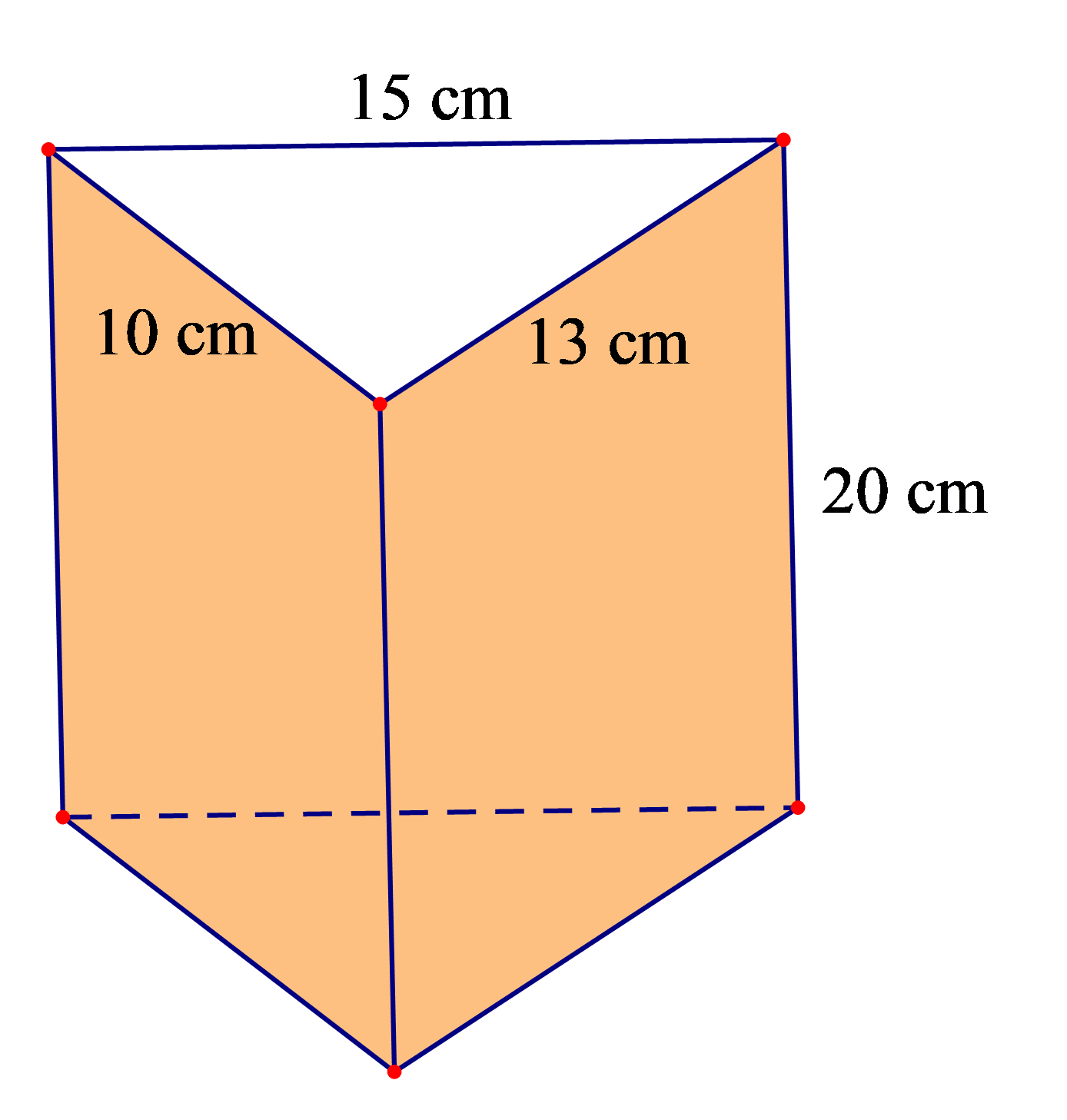
Hãy tính diện tích xung quanh của chiếc hộp.

Hướng dẫn giải

Ta có chu vi đáy của hình lăng trụ đứng tam giác là:

C_đáy = 10 + 13 + 15 = 38 (cm)

Diện tích xung quanh của hình lăng trụ đứng tam giác là:

S_xq = C_đáy . h = 38 . 20 = 760 (cm²).

Vậy diện tích xung quanh của chiếc hộp là 760 cm².

Bài 2. Lòng trong của một chiếc bể chứa nước có dạng hình lăng trụ đứng tứ giác, đáy là hình vuông có cạnh bằng 5 m, chiều cao của bể là 2,5 m. Hỏi bể chứa tối đa được bao nhiêu lít nước.

Hướng dẫn giải

Thể tích nước tối đa bể chứa được bằng thể tích của lòng trong của bể.

Lòng trong của bể hình lăng trụ đứng đáy là hình vuông nên ta có:

S_đáy = 5 . 5 = 25 (m²)

Thể tích lòng trong của bể là:

V = S_đáy . h = 25 . 2,5 = 62,5 (m³) = 62 500 (l).

Vậy bể chứa tối đa được 62 500 lít nước.

Xem thêm Lý thuyết các bài Toán 7 Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Bài 3. Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác

Lý thuyết Ôn tập chương 3

Lý thuyết Bài 1: Các góc ở vị trí đặc biệt

Lý thuyết Bài 2: Tia phân giác

Lý thuyết Bài 3: Hai đường thẳng song song