Toptailieu.vn biên soạn và giới thiệu Lý thuyết Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh (Cánh Diều) Toán 7 hay, ngắn gọn và bài tập tự luyện có lời giải chi tiết sẽ giúp học sinh nắm vững nội dung kiến thức từ đó dễ dàng làm các bài tập Toán 7.

Lý thuyết Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh (Cánh Diều) Toán 7

A. Lý thuyết

1. Trường hợp bằng nhau cạnh – góc – cạnh (c.g.c)

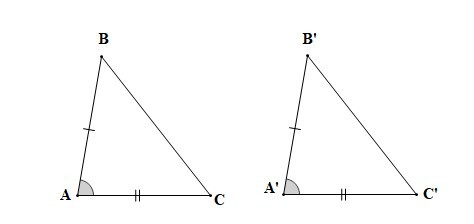
– Tính chất: Nếu hai cạnh và góc xen giữa của tam giác này lần lượt bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.

Nếu AB = A’B’, $\widehat{\mathrm{A}}=\widehat{\mathrm{A}\text{'}}$, AC = A’C’ thì DABC = DA’B’C’ (c.g.c).

Ví dụ: Biết chỉ cần thêm một điều kiện thì hai tam giác trong mỗi hình dưới đây là hai tam giác bằng nhau theo trường hợp cạnh – góc – cạnh. Hãy nêu điều kiện đó tương ứng cho mỗi hình.

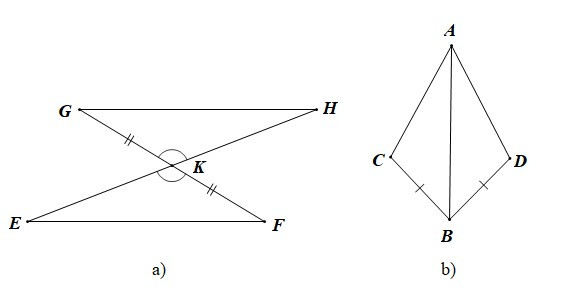
Hướng dẫn giải

a) Ta có: $\widehat{\mathrm{GKH}}=\widehat{\mathrm{EKF}}$ (đối đỉnh) và KG = KF.

Để DKGH và DKEF bằng nhau theo trường hợp cạnh – góc – cạnh thì điều kiện còn thiếu là điều kiện về cạnh sao cho cặp góc bằng nhau là góc xen giữa hai cặp cạnh bằng nhau.

Mà $\widehat{\mathrm{GKH}}$ của DKGH xen giữa hai cạnh KG và KH;

$\widehat{\mathrm{EKF}}$ của DKEF xen giữa hai cạnh KE và KF.

Do đó điều kiện còn thiếu là KH = KE.

Vậy điều kiện cần thêm để DKGH = DKFE là KH = KE.

b) Ta có: BC = BD và AB là cạnh chung.

Để DABC và DABD bằng nhau theo trường hợp cạnh – góc – cạnh thì điều kiện còn thiếu là điều kiện về góc sao cho cặp góc bằng nhau là góc xen giữa hai cặp cạnh bằng nhau.

Mà góc xen giữa hai cạnh BC và BA của DABC là $\widehat{\mathrm{ABC}};$

Góc xen giữa hai cạnh BD và BA của DABD là $\widehat{\mathrm{ABD}}.$

Do đó điều kiện còn thiếu là $\widehat{\mathrm{ABC}}=\widehat{\mathrm{ABD}}.$

Vậy điều kiện cần thêm để DABC = DABD là $\widehat{\mathrm{ABC}}=\widehat{\mathrm{ABD}}.$

Ví dụ: Cho tam giác ABC (AB < AC) có tia phân giác góc A cắt BC tại D. Trên cạnh AC lấy điểm E sao cho AB = AE. Chứng minh rằng:

a) DABD = DAED.

b) DA là tia phân giác của $\widehat{\mathrm{BDE}}.$

Hướng dẫn giải

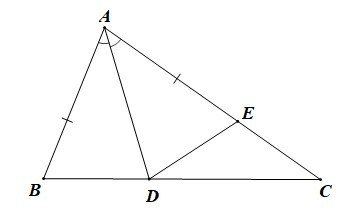
Xét DABD và DAED có:

AB = AE (giả thiết),

$\widehat{\mathrm{BAD}}=\widehat{\mathrm{EAD}}$ (do AD là tia phân giác $\widehat{\mathrm{BAC}}$),

AD là cạnh chung.

Do đó DABD = DAED (c.g.c)

Vậy DABD = DAED (c.g.c).

b) Vì DABD = DAED (chứng minh phần a)

Suy ra $\widehat{\mathrm{BDA}}=\widehat{\mathrm{EDA}}$ (hai góc tương ứng)

Do đó DA là tia phân giác của $\widehat{\mathrm{BDE}}.$

Vậy DA là tia phân giác của $\widehat{\mathrm{BDE}}.$

2. Áp dụng vào trường hợp bằng nhau về hai cạnh góc vuông của tam giác vuông

– Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

Nếu $\widehat{\mathrm{A}}=\widehat{\mathrm{A}\text{'}}=90°,$AB = A’B’, AC = A’C’ thì DABC = DA’B’C’.

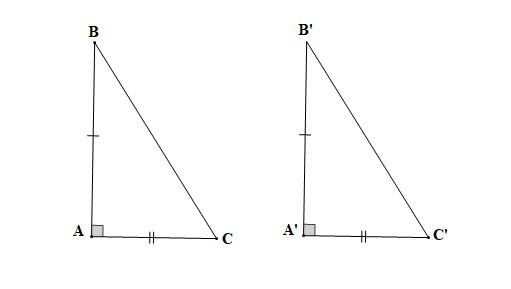
Ví dụ: Cho tam giác ABC có AH ⊥ BC (H ∈ BC) và H là trung điểm của BC. Biết AB = 3 cm. Tính AC.

Hướng dẫn giải

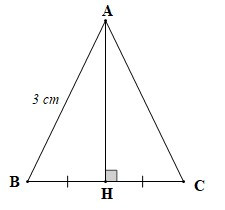
Xét DABH và DACH có:

$\widehat{\mathrm{AHB}}=\widehat{\mathrm{CHA}}=90°$ (giả thiết),

AH là cạnh chung,

BH = CH (giả thiết),

Do đó DABH = DACH (hai cạnh góc vuông).

Suy ra AB = AC (hai cạnh tương ứng) .

Mà AB = 3 cm nên AC = 3 cm.

Vậy độ dài cạnh AC là 3 cm.

3. Vẽ tam giác khi biết hai cạnh và góc xen giữa

Để vẽ tam giác ABC có AB = 3 cm, AC = 5 cm, $\widehat{\mathrm{A}}=50°$bằng thước thẳng (có chia đơn vị) và thước đo góc, ta làm như sau:

– Bước 1: Vẽ $\widehat{\mathrm{xAy}}=50°$

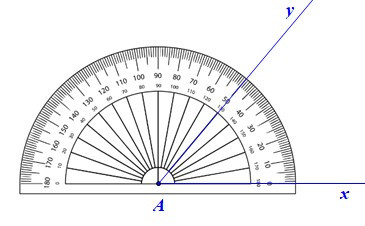
– Bước 2: Trên tia Ax lấy điểm B sao cho AB = 3 cm, trên tia Ay lấy điểm C sao cho AC = 5 cm

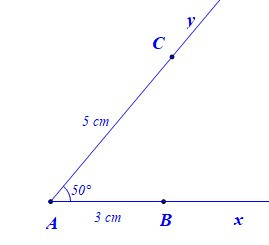
– Bước 3: Vẽ đoạn thẳng BC. Ta được tam giác ABC.

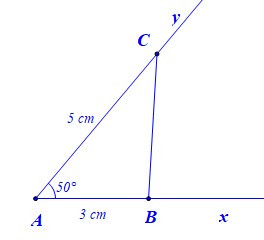
B. Bài tập tự luyện

B.1 Bài tập tự luận

Bài 1. Để đo khoảng cách giữa hai xã A và B bị ngăn cách bởi con sông người ta chọn các vị trí I, H, K ngoài con sông sao cho: I không thuộc đường thẳng AB, I là trung điểm của BH và AK, người ta đo được khoảng cách HK là 1 km. Khoảng cách giữa hai xã A, B là bao nhiêu?

Hướng dẫn giải

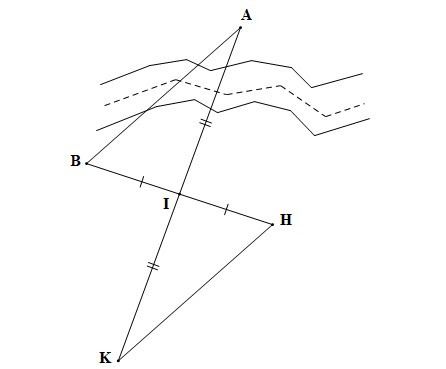
Xét DABI và DKHI có:

IA = IK (vì I là trung điểm của AK),

$\widehat{\mathrm{AIB}}=\widehat{\mathrm{HIK}}$ (hai góc đối đỉnh),

IB = IH (vì I là trung điểm của BH),

Do đó DABI = DKHI (c.g.c)

Suy ra AB = KH (hai cạnh tương ứng)

Mà HK = 1 km nên AB = 1 km.

Vậy khoảng cách giữa hai xã A và B là 1 km.

Bài 2. Cho tam giác ABC có $\widehat{\mathrm{B}}=90°,$ AC = 2AB. Gọi D là trung điểm của AC và tia AE là tia phân giác của $\widehat{\mathrm{BAC}}$ (E ∈ BC).

a) Chứng minh ED ⊥ AC;

b) Chứng minh EA = EC;

c) Tính số đo của $\widehat{\mathrm{BAC}},\widehat{\mathrm{BCA}}$ của DABC.

Hướng dẫn giải

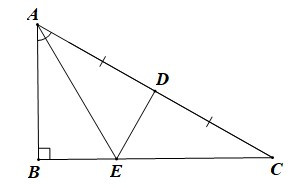
Vì AC = 2AB (giả thiết) nên AB = $\frac{1}{2}$AC.

Vì D là trung điểm AC nên AD = DC = $\frac{1}{2}$AC.

Do đó AB = AD = DC = $\frac{1}{2}$AC.

Xét DABE và DADE có:

AB = AD (chứng minh trên),

$\widehat{\mathrm{BAE}}=\widehat{\mathrm{DAE}}$ (do AE là tia phân giác của $\widehat{\mathrm{BAC}})$

AE là cạnh chung

Do đó DABE = DADE (c.g.c).

Suy ra $\widehat{\mathrm{ABE}}=\widehat{\mathrm{ADE}}$ (hai góc tương ứng)

Mà $\widehat{\mathrm{ABE}}=90°$ (giả thiết)

Do đó $\widehat{\mathrm{ADE}}=90°.$

Hay ED ⊥ AC tại D.

Vậy ED ⊥ AC.

b) Xét DADE và DCDE có:

$\widehat{\mathrm{ADE}}=\widehat{\mathrm{CDE}}=90°$ (do ED ⊥ AC),

AD = DC (chứng minh phần a),

ED là cạnh chung,

Do đó DADE = DCDE (hai cạnh góc vuông)

Suy ra EA = EC (hai cạnh tương ứng).

Vậy EA = EC.

c) Vì DADE = DCDE (chứng minh phần b)

Nên $\widehat{\mathrm{DAE}}=\widehat{\mathrm{DCE}}$ (hai góc tương ứng)

Mà $\widehat{\mathrm{DAE}}=\widehat{\mathrm{BAE}}$ (do AE là tia phân giác của $\widehat{\mathrm{BAC}}$)

Do đó $\widehat{\mathrm{DAE}}=\widehat{\mathrm{DCE}}=\widehat{\mathrm{BAE}}.$

Xét DABC vuông tại B có: $\widehat{\mathrm{BAC}}+\widehat{\mathrm{ACB}}=90°$ (hai góc nhọn trong tam giác vuông bằng 90°).

Suy ra $\widehat{\mathrm{BAE}}+\widehat{\mathrm{DAE}}+\widehat{\mathrm{DCE}}=90°$

Hay $3\widehat{\mathrm{DCE}}=90°$

Do đó $\widehat{\mathrm{DCE}}=30°$ nên $\widehat{\mathrm{BCA}}=30°$

Suy ra $\widehat{\mathrm{DAE}}=\widehat{\mathrm{BAE}}=30°$

Khi đó $\widehat{\mathrm{BAC}}=\widehat{\mathrm{BAE}}+\widehat{\mathrm{DAE}}=30°+30°=60°.$

Vậy DABC có $\widehat{\mathrm{BAC}}=60°$ và $\widehat{\mathrm{BCA}}=30°.$

Bài 3. Cho tam giác ABC nhọn (AB < AC). Gọi M, N lần lượt là trung điểm của AB, AC. Trên tia đối của MC lấy E sao cho CM = ME. Trên tia đối của NB lấy F sao cho NF = NB. Chứng minh rằng ba điểm E, A, F thẳng hàng.

Hướng dẫn giải

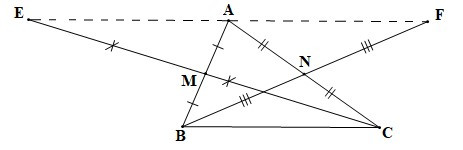
• Xét DANF và DCNB có:

NA = NC (vì N là trung điểm của AC),

$\widehat{\mathrm{ANF}}=\widehat{\mathrm{BNC}}$ (hai góc đối đỉnh),

FN = BN (giả thiết),

Do đó DANF = DCNB (c.g.c)

Suy ra $\widehat{\mathrm{AFN}}=\widehat{\mathrm{CBN}}$ (hai góc tương ứng)

Mà hai góc này ở vị trí so le trong của AF và BC.

Nên AF // BC                   (1)

• Xét DAME và DBMC có:

MA = MB (vì M là trung điểm của AB),

$\widehat{\mathrm{AME}}=\widehat{\mathrm{BMC}}$ (hai góc đối đỉnh),

EM = MC (giả thiết),

Do đó DAME = DBMC (c.g.c)

Suy ra $\widehat{\mathrm{AEM}}=\widehat{\mathrm{BCM}}$ (hai góc tương ứng)

Mà hai góc này ở vị trí so le trong của AE và BC.

Nên AE // BC                   (2)

Qua điểm A nằm ngoài đường thằng BC chỉ có duy nhất một đường thẳng song song với BC (tiên đề Euclid)       (3)

Từ (1), (2) và (3) suy ra AE ≡ AF.

Hay ba điểm A, E, F cũng nằm trên một đường thẳng.

Vậy ba điểm A, E, F thẳng hàng.

B.2 Bài tập trắc nghiệm

Câu 1. Cho hình vẽ sau:

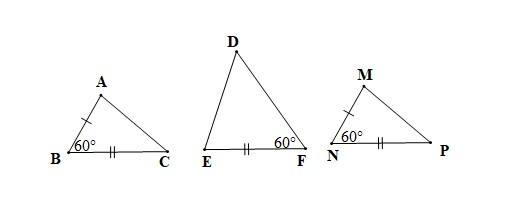
Khẳng định nào sau đây là đúng?

A. DABC = DMNP;

B. DABC = DDEF;

C. DMNP = DDEF;

D. DABC = DMNP = DDEF.

Hướng dẫn giải

Đáp án đúng là: A

Xét DABC và DMNP có:

BA = MN (giả thiết),

$\widehat{\mathrm{B}}=\widehat{\mathrm{N}}$ (giả thiết),

CB = NP (giả thiết)

Do đó DABC = DMNP (c.g.c)

Vậy ta chọn phương án A.

Câu 2. Cho hình vuông ABCD, trên cạnh AD lấy điểm E, trên cạnh DC lấy điểm F và trên cạnh BC lấy điểm G sao cho AE = DF = CG. Số đo góc GFE là:

A. 45°;

B. 90°;

C. 60°;

D. 100°.

Hướng dẫn giải

Đáp án đúng là: B

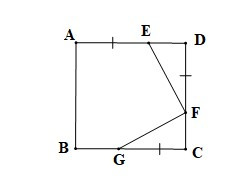
Vì ABCD là hình vuông (giả thiết) nên AD = CD (tính chất hình vuông)

Do đó AE + ED = CF + FD

Mà AE = FD (giả thiết) nên ED = CF.

Xét DFED và DGFC có:

FD = CG (giả thiết),

$\widehat{\mathrm{D}}=\widehat{\mathrm{C}}$ ($=90°,$ tính chất hình vuông),

ED = CF (chứng minh trên)

Do đó DFED = DGFC (hai cạnh góc vuông)

Suy ra $\widehat{\mathrm{F}\text{ED}}=\widehat{\mathrm{CFG}}$ (hai góc tương ứng)

Mà $\widehat{\mathrm{F}\text{ED}}+\widehat{\mathrm{DF}\text{E}}=90°$ (trong tam giác FDE vuông tại D, hai góc nhọn phụ nhau)

Do đó $\widehat{\mathrm{GFC}}+\widehat{\mathrm{DF}\text{E}}=90°$

Mặt khác $\widehat{\mathrm{GFC}}+\widehat{\mathrm{DF}\text{E}}+\widehat{\mathrm{GF}\text{E}}=180°$

Suy ra $\widehat{\mathrm{GF}\text{E}}=180°-\left(\widehat{\mathrm{GFC}}+\widehat{\mathrm{DF}\text{E}}\right)=180°-90°=90°$

Vậy $\widehat{\mathrm{GF}\text{E}}=90°.$ 

Câu 3. Cho góc xOy tù, gọi Oz là tia phân giác của góc xOy. Trên tia Ox lấy điểm M, trên tia Oy lấy điểm N sao cho OM = ON. Trên tia đối của tia Oz lấy điểm I tuỳ ý. Chọn phát biểu đúng nhất:

A. $\widehat{\mathrm{MOI}}=\widehat{\mathrm{NOI}};$ 

B. IM = IN;

C. IO là tia phân giác của $\widehat{\mathrm{MOI}}=\widehat{\mathrm{NOI}};$ 

D. Cả A, B, C đều đúng.

Hướng dẫn giải

Đáp án đúng là: D

Vì tia Oz là tia phân giác của góc xOy nên $\widehat{\mathrm{xOz}}=\widehat{\mathrm{yOz}}$ (tính chất tia phân giác của một góc)

Mà $\widehat{\mathrm{xOz}}+\widehat{\mathrm{xOI}}=180°$ (tính chất hai góc kề bù) và $\widehat{\mathrm{yOz}}+\widehat{\mathrm{yOI}}=180°$ (tính chất hai góc kề bù)

Do đó $\widehat{\mathrm{xOI}}=\widehat{\mathrm{yOI}}$ hay $\widehat{\mathrm{MOI}}=\widehat{\mathrm{NOI}}$ 

Xét DMOI và DNOI có:

OM = ON (giả thiết),

$\widehat{\mathrm{MOI}}=\widehat{\mathrm{NOI}}$ (chứng minh trên),

OI là cạnh chung

Do đó DMOI = DNOI (c.g.c)

Suy ra IM = IN (hai cạnh tương ứng) và $\widehat{\mathrm{MI}\text{O}}=\widehat{\mathrm{NI}\text{O}}$ (hai góc tương ứng)

Vì $\widehat{\mathrm{MI}\text{O}}=\widehat{\mathrm{NI}\text{O}}$ nên tia IO là tia phân giác của $\widehat{\mathrm{MIN}}.$

Vậy ta chọn phương án D.

Xem thêm các bài lý thuyết Toán 7 Cánh Diều hay, chi tiết khác:

Lý thuyết Bài 4. Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh

Lý thuyết Bài 6. Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc

Lý thuyết Bài 7. Tam giác cân

Lý thuyết Bài 8. Đường vuông góc và đường xiên

Lý thuyết Bài 9. Đường trung trực của một đoạn thẳng