Với giải Bài 15 trang 60 Toán 8 Tập 2 Chân trời sáng tạo Bài tập cuối chương 7 giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:
Bài 15 trang 60 Toán 8 Tập 2 | Chân trời sáng tạo Giải Toán lớp 8
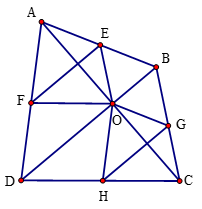
Bài 15 trang 60 Toán 8 Tập 2: Cho tứ giác ABCD có AC và BD cắt nhau tại O. Qua O, kẻ đường thẳng song song với BC cắt AB tại E, kẻ đường thẳng song song với CD cắt AD tại F.
a) Chứng minh FE // BD;
b) Từ O kẻ đường thẳng song song với AB cắt BC tại G và đường thẳng song song với AD cắt CD tại H. Chứng minh rằng CG.DH = BG.CH.
Lời giải:
a) Tam giác ABC có OE // BC (gt)
Suy ra (theo định lí Thalès) (1)
Tam giác ADC có OF // CD (gt)
Suy ra (theo định lí Thalès) (2)
Từ (1) và (2) suy ra
Tam giác ADB có
Suy ra EF // BD (theo định lí Thalès đảo)
b) Tam giác ABC có OG // AB (gt)
Suy ra (theo định lí Thalès) (3)
Tam giác ACD có OH // AD (gt)
Suy ra (theo định lí Thalès) (4)
Từ (3) (4) suy ra ⇒ CG.DH = BG.CH
Xem thêm Lời giải bài tập Toán 8 Chân trời sáng tạo hay, chi tiết khác:
Bài 1 trang 58 Toán 8 Tập 2: Cho tam giác ABC, biết DE // BC và AE = 6 cm, EC = 3 cm, DB = 2 cm (Hình 1). Độ dài đoạn thẳng AD là
Bài 2 trang 58 Toán 8 Tập 2: Cho tam giác ABC, biết DE // BC (Hình 2). Trong các khẳng định sau, khẳng định nào sai?
Bài 3 trang 58 Toán 8 Tập 2: Cho Hình 3, biết AM = 3 cm, MN = 4 cm, AC = 9 cm. Giá trị của biểu thức x – y là:
Bài 4 trang 58 Toán 8 Tập 2: Cho tam giác MNP có MD là tia phân giác của góc M (D ∈ NP). Trong các khẳng định sau, khẳng định nào đúng?
Bài 5 trang 58 Toán 8 Tập 2: Cho hai đoạn thẳng AB = 12 cm và CD = 18 cm. Tỉ số của hai đoạn thẳng AB và CD là
Bài 6 trang 58 Toán 8 Tập 2: Cho Hình 4, biết MN // BC, AN = 4 cm. NC = 8 cm, MN = 5 cm. Độ dài cạnh BC là
Bài 7 trang 59 Toán 8 Tập 2: Cho Hình 5, biết MN // DE, MN = 6 cm, MP = 3 cm, PE = 5 cm. Độ dài đoạn thẳng DE là
Bài 8 trang 59 Toán 8 Tập 2: Cho tam giác ABC, một đường thẳng song song với BC cắt AB và AC lần lượt tại D và E. Qua E kẻ đường thẳng song song với CD cắt AB tại F. Biết AB = 25 cm, AF = 9 cm, EF = 12 cm, độ dài đoạn DC là
Bài 9 trang 59 Toán 8 Tập 2: Cho tam giác ABC biết AM là đường phân giác. Trong các khẳng định sau, khẳng định nào đúng?
Bài 10 trang 59 Toán 8 Tập 2: Cho tam giác ABC và điểm D trên cạnh AB sao cho AD = 13,5 cm, DB = 4,5 cm. Tính tỉ số các khoảng cách từ các điểm D và B đến cạnh AC.
Bài 11 trang 59 Toán 8 Tập 2: a) Độ cao AN và chiều dài bóng nắng của các đoạn thẳng AN, BN trên mặt đất được ghi lại như trong Hình 6. Tìm chiều cao AB của cái cây.
Bài 12 trang 59 Toán 8 Tập 2: Cho tam giác ABC có BC bằng 30 cm. Trên đường cao AH lấy các điểm K, I sao cho AK = KI = IH. Qua I và K vẽ các đường EF // BC, MN // BC (E, M ∈ AB; F, N ∈ AC).
Bài 13 trang 60 Toán 8 Tập 2: Tính độ dài x trong Hình 8.
Bài 14 trang 60 Toán 8 Tập 2: Tính độ dài x trong Hình 9.
Bài 15 trang 60 Toán 8 Tập 2: Cho tứ giác ABCD có AC và BD cắt nhau tại O. Qua O, kẻ đường thẳng song song với BC cắt AB tại E, kẻ đường thẳng song song với CD cắt AD tại F.
Bài 16 trang 60 Toán 8 Tập 2: Cho hình bình hành ABCD. Đường thẳng a đi qua A cắt BD, BC, DC lần ượt tại E, K, G (Hình 10). Chứng minh rằng:
Bài 17 trang 60 Toán 8 Tập 2: a) Quan sát Hình 11, chứng minh AK là đường phân giác của góc A trong tam giác ABC.
Xem thêm Lời giải bài tập Toán 8 Chân trời sáng tạo hay, chi tiết khác:
Bài 3: Tính chất đường phân giác của tam giác
Bài tập cuối chương 7
Bài 1: Hai tam giác đồng dạng
Bài 2: Các trường hợp đồng dạng của hai tam giác
Bài 3: Các trường hợp đồng dạng của hai tam giác vuông
