Toptailieu.vn biên soạn và giới thiệu lời giải SBT Tin học 11 (Kết nối tri thức) Bài 24: Đánh giá độ phức tạp thời gian thuật toán hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi sách bài tập Tin học 11 Bài 24 từ đó học tốt môn Tin học 11.
Nội dung bài viết
SBT Tin học 11 (Kết nối tri thức) Bài 24: Đánh giá độ phức tạp thời gian thuật toán
T1 = thời gian chương trình nhập dữ liệu input và đưa vào bộ nhớ.
T2 = thời gian chạy chương trình từ khi nhập xong dữ liệu input và tính xong dữ liệu output.
T3 = thời gian đưa dữ liệu output ra thiết bị ngoài chuẩn.
Khi đó thời gian chạy chương trình T(n) dùng để tính độ phức tạp thời gian của thuật toán là phương án nào trong các phương án sau?
A. T1 + T2.
B. T2.
C. T2+T3.
Lời giải:
Đáp án đúng là: B. T2. T2 = thời gian chạy chương trình từ khi nhập xong dữ liệu input và tính xong dữ liệu output.
Câu 24.2 trang 76 SBT Tin học 11: Đánh giá thời gian chạy của chương trình sau:

Lời giải:
Đánh giá thời gian chạy của chương trình như sau: T(n) = n+2.
Câu 24.3 trang 76 SBT Tin học 11: Đánh giá thời gian chạy của chương trình sau:

Lời giải:
Đánh giá thời gian chạy của chương trình sau: T(n) = 2log2n + 2.

Lời giải:
Đánh giá thời gian chạy của chương trình sau, trong đó A là ma trận vuông bậc n.
T(n) = n2 + 2.

Lời giải:
T(n) = (3/2).n2 + (5/2)n + 1 trong trường hợp xấu nhất.
Lời giải:
T(n) = 2n2 – 3n + 2 trong trường hợp xấu nhất.
Lời giải:
T(n) = 2n2 – 2n + 1 trong trường hợp xấu nhất.
Câu 24.8 trang 77 SBT Tin học 11: Tính độ phức tạp của các hàm sau theo kí hiệu O-lớn
b) 2n2 + 3n3log(n) + n3/2.
c) 2" + 3" + 5".
Lời giải:
a) O(nlogn);
b) O(n3.logn);
c) O(5")
Câu 24.9 trang 77 SBT Tin học 11: a) Chứng minh n = O(n2).
Lời giải:
a) Vì hiển nhiên n < n với n > 1 nên suy ra n = O(n).
b) Nếu như n2 = O(n) thì ta phải có n2 < C.n với n đủ lớn, nhưng từ bất đẳng thức này suy ra n < C. Mâu thuẫn. Vậy suy ra n = O(n).
Lời giải:
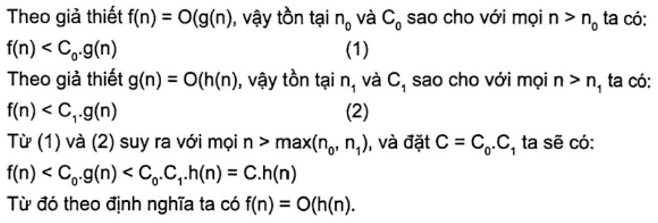
Xem thêm các bài giải sách bài tập Tin học 11 Kết nối tri thức hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.