Với giải Câu 25.4 trang 78 SBT Tin học 11 Kết nối tri thức chi tiết trong Bài 25: Thực hành xác định độ phức tạp thời gian thuật toán giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Tin học 11. Mời các bạn đón xem:
Em hãy xác định thời gian chạy T(n) của thuật toán sắp xếp chèn sau
Câu 25.4 trang 78 SBT Tin học 11: Em hãy xác định thời gian chạy T(n) của thuật toán sắp xếp chèn sau, với n là độ dài của dãy A.

Lời giải:
Gọi n là kích thước của mảng, T(n) là thời gian thực hiện của thuật toán. Thời gian chạy của thuật toán được phân tích như sau:
– Câu lệnh tại dòng 2 cần 1 đơn vị thời gian.
– Vòng lặp for tại dòng 3 biến i chạy từ 1 đến n − 1, nên vòng lặp có n – 1 bước lặp.
– Với mỗi bước lặp chương trình thực hiện:
• Hai lệnh gán tại dòng 4 và 5.
• Vòng lặp while tại dòng 6. Vòng lặp này sẽ chạy tối đa là i lần. Mỗi lần lặp chương trình sẽ thực hiện hai lệnh gán tại dòng 7 và 8, cần 2 đơn vị thời gian. • Lệnh gán tại dòng 9 cần 1 đơn vị thời gian.
Tổng hợp lại chương trình trên có thời gian chạy tối đa là:
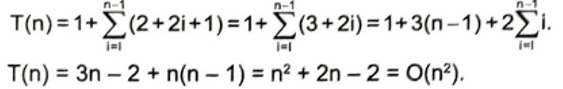
Xem thêm các bài giải sách bài tập Tin học 11 Kết nối tri thức hay, chi tiết khác:
Câu 25.1 trang 77 SBT Tin học 11: Tính độ phức tạp của các hàm thời gian sau: a) T(n) = n + 2log n.
Câu 25.2 trang 77 SBT Tin học 11: Cho biết thuật toán sau thực hiện công việc gì và hãy xác định độ phức tạp thời gian của thuật toán. 1 def findMax(A):
Câu 25.5 trang 78 SBT Tin học 11: Xác định độ phức tạp thời gian của hàm sau:
Câu 25.6 trang 78 SBT Tin học 11: Nếu f(n) = O(g(n)) thì có suy ra được g(n) = O(f(n)) hay không?
Câu 25.7 trang 78 SBT Tin học 11: Giả sử f(n) = . Chứng minh rằng f(n) = O(n)
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.