Bất phương trình mũ và lôgarit (Lý thuyết + 50 bài tập có lời giải)

A. Tóm tắt lý thuyết

1. Bất phương trình mũ:

    • Khi giải bất phương trình mũ, ta cần chú ý đến tính đơn điệu của hàm số mũ.

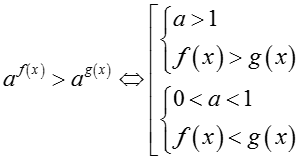    . Tương tự với bất phương trình dạng: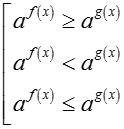 

    • Trong trường hợp cơ số a có chứa ẩn số thì: a^M > a^N ⇔ (a - 1)(M - N) > 0 .

    • Ta cũng thường sử dụng các phương pháp giải tương tự như đối với phương trình mũ:

        + Đưa về cùng cơ số.

        + Đặt ẩn phụ.

        + Sử dụng tính đơn điệu 

2. Bất phương trình lôgarit:

    • Bất phương trình lôgarit cơ bản có dạng: log_af(x) > b; log_af(x) ≥ b; log_af(x) < b; log_af(x) ≤ b

    Phương pháp giải bất phương trình lôgarit

    • Đưa về cùng cơ số

    - Nếu a > 1 thì log_af(x) > log_ag(x) ⇔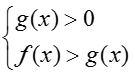 

    - Nếu 0 < a < 1 thì log_af(x) > log_ag(x) ⇔ 1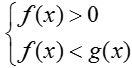

    • Đặt ẩn phụ

    • Mũ hóa

B. Bài tập trắc nghiệm 

Câu 46. (ĐỀ MINH HỌA 2016 – 2017)​​ Giải phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_4\left(x-1\right)=3$.

 A.​​ $x=63$.​​  B.​​ $x=65$.​​  C.​​ $x=80$.​​  D.​​ $x=82$.

Câu​​ 47.​​ Tìm tập nghiệm​​ $S$​​ của phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_6\left[x\left(5-x\right)\right]=1.$

 A.​​ $S=\left\{2;3\right\}.$ B.​​ $S=\left\{4;6\right\}$.​​  C.​​ $S=\left\{1;-6\right\}$.​​  D.​​ $S=\left\{-1;6\right\}$.

Câu​​ 48.​​ Phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(x-3\sqrt{x}+4\right)=3$​​ có tất cả bao nhiêu nghiệm?

 A.​​ 4.​​  B. 1.​​  C. 2.​​  D.​​ 0.

Câu​​ 49.​​ Tính​​ $P$​​ là tích tất cả các nghiệm của phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_{\frac{1}{2}}\frac{x^2-3x+2}{x}=0.$

 A.​​ $P=4.$​​  B.​​ $P=2\sqrt{2}.$ C.​​ $P=2.$​​  D.​​ $P=1.$

Câu​​ 50.​​ Phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(x-3\right)+2\mathrm{l}\mathrm{o}{\mathrm{g}}_{4}3.\mathrm{l}\mathrm{o}{\mathrm{g}}_{3}x=2$​​ có​​ tất cả bao nhiêu nghiệm?

 A. 1. B. 2. C. 3. D.​​ 0.

Câu​​ 51.​​ Biết​​ rằng​​ phương trình​​ $2\mathrm{l}\mathrm{o}\mathrm{g}\left(x+2\right)+\mathrm{l}\mathrm{o}\mathrm{g}4=\mathrm{l}\mathrm{o}\mathrm{g}x+4\mathrm{l}\mathrm{o}\mathrm{g}3$​​ có hai nghiệm​​ phân biệt​​ $x_1,x_2\mathrm{ }\mathrm{ }\left(x_1<x_2\right)$. Tính​​ $P=\frac{x_1}{x_2}.$

 A.​​ $P=4.$ B.​​ $P=\frac{1}{4}.$ C.​​ $P=64.$ D.​​ $P=\frac{1}{64}.$

Câu​​ 52.​​ Biết​​ rằng​​ phương trình​​ ${\left[\mathrm{l}\mathrm{o}{\mathrm{g}}_{\frac{1}{3}}\left(9x\right)\right]}^2+\mathrm{l}\mathrm{o}{\mathrm{g}}_3\frac{x^2}{81}-7=0$​​ có hai nghiệm​​ phân biệt​​ $x_1,x_2$. Tính​​ $P=x_1{x}_2.$

 A.​​ $P=\frac{1}{9^3}.$ B.​​ $P=3^6.$ C.​​ $P=9^3.$ D.​​ $P=3^8.$

Câu 53. (ĐỀ CHÍNH THỨC 2016 – 2017)​​ Tìm tập nghiệm​​ $S$​​ của phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_{\sqrt{2}}\left(x-1\right)+\mathrm{l}\mathrm{o}{\mathrm{g}}_{\frac{1}{2}}\left(x+1\right)=1.$

 A.​​ $\mathit{S}=\left\{\frac{3+\sqrt{13}}{2}\right\}.$  B.​​ $\mathit{S}=\left\{3\right\}.$ 

 C.​​ $\mathit{S}=\left\{2-\sqrt{5};2+\sqrt{5}\right\}.$ D.​​ $\mathit{S}=\left\{2+\sqrt{5}\right\}.$

Câu 54.​​ Cho phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left[\mathrm{l}\mathrm{o}{\mathrm{g}}_{\frac{1}{8}}\left(x^3\right)+\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x+x+1\right]=3.$​​ Mệnh đề nào sau đây là đúng?

 A. Nghiệm của phương trình là số nguyên âm.

 B. Nghiệm của phương trình là số chính phương.

 C. Nghiệm của phương trình là số nguyên tố.​​  

 D. Nghiệm của phương trình là số vô tỉ.

Câu​​ 55.​​ Số nghiệm của phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_4\left(\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x\right)+\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(\mathrm{l}\mathrm{o}{\mathrm{g}}_{4}x\right)=2$​​ là:

 A. 0.​​  B. 1.​​  C. 2.​​  D. Nhiều hơn​​ $2$.

Câu 56.​​ Tính​​ $P$​​ tích tất cả các nghiệm của phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x-\mathrm{l}\mathrm{o}{\mathrm{g}}_{x}64=1.$

 A.​​ $P=1$.​​  B.​​ $P=2$.​​  C.​​ $P=4$.​​  D.​​ $P=8$.

Câu​​ 57.​​ Tìm tập nghiệm​​ $S$​​ của phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(9-2^x\right)=3-x.$​​ 

 A.​​ $S=\left\{-3;0\right\}.$​​  B.​​ $S=\left\{0;3\right\}.$ C.​​ $S=\left\{1;3\right\}.$ D.​​ $S=\left\{-3;1\right\}.$

Câu 58.​​ Biết rằng phương trình​​ $\mathrm{l}\mathrm{o}\mathrm{g}x.\mathrm{l}\mathrm{o}\mathrm{g}\left(100x^2\right)=4$​​ có hai nghiệm có dạng​​ $x_1$​​ và​​ $\frac{1}{x_2}$​​ trong đó​​ $x_1,x_2$​​ là những số nguyên. Mệnh đề nào sau đây là đúng?

 A.​​ $x_2=\frac{1}{x_1^2}$.​​  B.​​ $x_2=x_1^2$.​​  C.​​ $x_1.x_2=1$.​​  D.​​ $x_2=100x_1$.​​ 

Câu 59.​​ Phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_{2017}x+\mathrm{l}\mathrm{o}{\mathrm{g}}_{2016}x=0$​​ có tất cả bao nhiêu nghiệm?

 A.​​ 0. B.​​ 1. C.​​ 2. D.​​ 3.

Câu 60.​​ Cho phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_{4}x.\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(4x\right)+\mathrm{l}\mathrm{o}{\mathrm{g}}_{\sqrt{2}}\left(\frac{x^3}{2}\right)=0$. Nếu đặt​​ $t=\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x,$​​ ta được phương trình nào sau đây?

 A.​​ $t^2+14t-4=0.$ B.​​ $t^2+11t-3=0.$ 

 C.​​ $t^2+14t-2=0.$ D.​​ $t^2+11t-2=0.$

Câu 61.​​ Tổng lập phương các nghiệm của phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x.\mathrm{l}\mathrm{o}{\mathrm{g}}_3\left(2x-1\right)=2\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x$​​ bằng:

 A.​​ $6$.​​  B.​​ $26$.​​  C.​​ $126$.​​  D.​​ $216$.

Câu 62.​​ Biết rằng phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_3\left(3^{x+1}-1\right)=2x+\mathrm{l}\mathrm{o}{\mathrm{g}}_{\frac{1}{3}}2$​​ có hai nghiệm​​ $x_1$​​ và​​ $x_2.$​​ Hãy tính tổng​​ $S=27^{x_1}+27^{x_2}.$​​ 

 A.​​ $S=180.$​​  B.​​ $S=45.$​​  C.​​ $S=9.$​​  D.​​ $S=252.$​​ 

Câu 63.​​ Số nghiệm của phương trình​​ $\frac{x^3-5x^2+6x}{\mathrm{l}\mathrm{n}\left(x-1\right)}=0$​​ là:

 A. 0.​​  B. 1.​​  C. 2. C. 3.

Câu 64.​​ Biết rằng phương trình​​ $2\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x+\mathrm{l}\mathrm{o}{\mathrm{g}}_{\frac{1}{2}}\left(1-\sqrt{x}\right)=\frac{1}{2}\mathrm{l}\mathrm{o}{\mathrm{g}}_{\sqrt{2}}\left(x-2\sqrt{x}+2\right)$​​ có nghiệm duy nhất có dạng​​ $a+b\sqrt{3}$​​ với​​ $a,b\in \mathbb{Z}$. Tính tổng​​ $S=a+b.$

 A.​​ $S=6.$ ​​​​  B.​​ $S=2.$ ​​​​  C.​​ $S=-2.$ ​​​​  D.​​ $S=-6.$ ​​​​ 

Câu 65.​​ Phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_3\frac{x^2-2x+1}{x}+x^2+1=3x$​​ có tổng tất cả các nghiệm bằng:​​ 

 A.​​ 3.​​  B.​​ 5. C.​​ $\sqrt{5}$. ​​  D.​​ 2.

Câu 66. (ĐỀ MINH HỌA 2016 – 2017)​​ Giải bất phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(3x-1\right)>3$.​​ 

 A.​​ $x>3$.​​  B.​​ $\frac{1}{3}<x<3$. C.​​ $x<3$.​​  D.​​ $x>\frac{10}{3}$.

Câu​​ 67.​​ Cho bất phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_{\frac{1}{3}}\left(x^2-2x+6\right)\le -2$. Mệnh đề nào sau đây là đúng?

 A.​​ Tập nghiệm của bất phương trình​​ là nửa khoảng.  

 B.​​ Tập nghiệm của bất phương trình​​ là một đoạn.

 C.​​ Tập nghiệm của bất phương trình​​ là hợp của hai nửa khoảng.​​ 

 D.​​ Tập nghiệm của bất phương trình​​ là hợp của hai đoạn.

Câu 68.​​ Gọi​​ $M\left(x_0;y_0\right)$​​ là điểm thuộc đồ thị hàm số​​ $y=\mathrm{l}\mathrm{o}{\mathrm{g}}_{3}x$. Tìm điều kiện của​​ $x_0$​​ để điểm​​ $M$​​ nằm phía trên đường thẳng​​ $y=2$.

 A.​​ $x_0>0$.​​  B.​​ $x_0>9$.​​  C.​​ $x_0>2$.​​  D.​​ $x_0<2$.

Câu 69.​​ Tìm tập nghiệm​​ $S$​​ của bất phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_{\frac{1}{5}}\left(x^2-1\right)<\mathrm{l}\mathrm{o}{\mathrm{g}}_{\frac{1}{5}}\left(3x-3\right).$

 A.​​ $S=\left(2;+\mathrm{\infty }\right).$  B.​​ $S=\left(-\mathrm{\infty };1\right)\cup \left(2;+\mathrm{\infty }\right).$

 C.​​ $S=\left(-\mathrm{\infty };-1\right)\cup \left(2;+\mathrm{\infty }\right).$ D.​​ $S=\left(1;2\right).$

Câu 70.​​ Tìm tập nghiệm​​ $S$​​ của bất phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_a\left(x^2-x-2\right)>\mathrm{l}\mathrm{o}{\mathrm{g}}_a\left(-x^2+2x+3\right)$, biết​​ $\frac{9}{4}$​​ thuộc​​ $S.$

 A.​​ $S=\left(2;\frac{5}{2}\right)$. B.​​ $S=\left(-1;\frac{5}{2}\right)$.​​  C.​​ $S=\left(-\mathrm{\infty };-1\right)$. D.​​ $S=\left(\frac{5}{2};+\mathrm{\infty }\right)$.

Câu​​ 71.​​ Tìm tập nghiệm​​ $S$​​ của bất phương trình​​ $\mathrm{l}\mathrm{n}{x}^2>\mathrm{l}\mathrm{n}\left(4x-4\right).$

 A.​​ $S=\left(2;+\mathrm{\infty }\right)$.​​  B.​​ $S=\left(1;+\mathrm{\infty }\right)$.​​  C.​​ $S=\mathbb{R}\backslash \left\{2\right\}$. D.​​ $S=\left(1;+\mathrm{\infty }\right)\backslash \left\{2\right\}.$

Câu​​ 72.​​ Gọi​​ $S$​​ là tập nghiệm của bất phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_{\mathrm{0,3}}\left(4x^2\right)\ge \mathrm{l}\mathrm{o}{\mathrm{g}}_{\mathrm{0,3}}\left(12x-5\right).$​​ Kí hiệu​​ $m,M$​​ lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của tập​​ $S$. Mệnh đề nào sau đây là đúng?

 A.​​ $m+M=3.$​​  B.​​ $m+M=2$.​​  C.​​ $M-m=3.$​​  D.​​ $M-m=1.$​​ 

Câu​​ 73.​​ Tìm tập nghiệm​​ $S$​​ của bất phương trình​​ $\mathrm{l}\mathrm{o}\mathrm{g}10^{\mathrm{l}\mathrm{o}\mathrm{g}\left(x^2+21\right)}<1+\mathrm{l}\mathrm{o}\mathrm{g}x.$

 A.​​ $S=\left(3;7\right).$  B.​​ $S=\left(-\mathrm{\infty };3\right)\cup \left(7;+\mathrm{\infty }\right).$

 C.​​ $S=\left(-\mathrm{\infty };3\right).$  D.​​ $S=\left(7;+\mathrm{\infty }\right).$

Câu 74.​​ Có bao nhiêu số nguyên dương​​ $x$​​ thỏa mãn bất phương trình​​ $\mathrm{l}\mathrm{o}\mathrm{g}\left(x-40\right)+\mathrm{l}\mathrm{o}\mathrm{g}\left(60-x\right)<2$?

 A.​​ 20. B.​​ 18. C.​​ 21. D.​​ 19.

Câu​​ 75.​​ Biết rằng tập nghiệm của bất phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(1+\mathrm{l}\mathrm{o}{\mathrm{g}}_{\frac{1}{9}}x-\mathrm{l}\mathrm{o}{\mathrm{g}}_{9}x\right)<1$​​ có dạng​​ $S=\left(\frac{1}{a};b\right)$​​ với​​ $a,b$​​ là những số nguyên. Mệnh đề nào sau đây là đúng?

 ​​ A.​​ $a=-b$.​​  B.​​ $a+b=1$.​​  C.​​ $a=b$.​​  D.​​ $a=2b$.​​ 

Câu​​ 76.​​ Có bao nhiêu giá trị nguyên của​​ $x$​​ trong đoạn​​ $\left[-2018;2018\right]$​​ thỏa mãn bất phương trình​​ $\mathrm{l}\mathrm{o}\mathrm{g}{}_{\frac{\pi }{4}}{}^{\mathrm{ }}\mathrm{ }\left[\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(x+\sqrt{2x^2-x}\right)\right]<0?$

 A.​​ $4033.$ B.​​ $4031.$ C.​​ $4037.$ D.​​ $2018.$

Câu​​ 77.​​ Tìm tập nghiệm​​ $S$​​ của bất phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x+\mathrm{l}\mathrm{o}{\mathrm{g}}_{3}x>1+\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x\mathrm{l}\mathrm{o}{\mathrm{g}}_{3}x.$

 A.​​ $S=\left(3;+\mathrm{\infty }\right).$  B.​​ $S=\left(0;2\right)\cup \left(3;+\mathrm{\infty }\right).$ 

 C.​​ $S=\left(2;3\right).$  D.​​ $S=\left(-\mathrm{\infty };2\right)\cup \left(3;+\mathrm{\infty }\right).$

Câu​​ 78.​​ Có tất cả bao nhiêu số nguyên thỏa mãn bất phương trình​​ $\mathrm{l}\mathrm{o}\mathrm{g}{}_{\frac{1}{2}}{}^{\mathrm{ }}\mathrm{ }\left[\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(2-x^2\right)\right]>0$?

 ​​ A.​​ $1$.​​  B.​​ $2$.​​  C.​​ $3$.​​  D.​​ $0$.​​ 

Câu 79.​​ Tìm tập nghiệm​​ $S$​​ của bất phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_{\frac{1}{2}}\left(\mathrm{l}\mathrm{o}{\mathrm{g}}_3\frac{2x+1}{x-1}\right)>0.$

 ​​ ​​ ​​ ​​​​  A.​​ $S=\left(-\mathrm{\infty };1\right)\cup \left(4;+\mathrm{\infty }\right).$ B.​​ $S=\left(-\mathrm{\infty };-2\right)\cup \left(1;+\mathrm{\infty }\right).$​​   ​​​​  

 C.​​ $S=\left(-2;1\right)\cup \left(1;4\right).$​​  D.​​ $S=\left(-\mathrm{\infty };-2\right)\cup \left(4;+\mathrm{\infty }\right).$

Câu​​ 80.​​ Tìm tập nghiệm​​ $S$​​ của bất phương trình​​ $\frac{1-\mathrm{l}\mathrm{o}{\mathrm{g}}_{4}x}{1-\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x}\le \frac{1}{2}.$

 A.​​ $S=\left(0;2\right).$​​  B.​​ $S=\left[2;+\mathrm{\infty }\right).$ C.​​ $S=\left(-\mathrm{\infty };2\right).$ D.​​ $S=\left(2;+\mathrm{\infty }\right).$

Câu 46. (ĐỀ MINH HỌA 2016 – 2017)​​ Giải phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_4\left(x-1\right)=3$.

 A.​​ $x=63$.​​  B.​​ $x=65$.​​  C.​​ $x=80$.​​  D.​​ $x=82$.

Câu​​ 47.​​ Tìm tập nghiệm​​ $S$​​ của phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_6\left[x\left(5-x\right)\right]=1.$

 A.​​ $S=\left\{2;3\right\}.$ B.​​ $S=\left\{4;6\right\}$.​​  C.​​ $S=\left\{1;-6\right\}$.​​  D.​​ $S=\left\{-1;6\right\}$.

Câu​​ 48.​​ Phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(x-3\sqrt{x}+4\right)=3$​​ có tất cả bao nhiêu nghiệm?

 A.​​ 4.​​  B. 1.​​  C. 2.​​  D.​​ 0.

Câu​​ 49.​​ Tính​​ $P$​​ là tích tất cả các nghiệm của phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_{\frac{1}{2}}\frac{x^2-3x+2}{x}=0.$

 A.​​ $P=4.$​​  B.​​ $P=2\sqrt{2}.$ C.​​ $P=2.$​​  D.​​ $P=1.$

Câu​​ 50.​​ Phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(x-3\right)+2\mathrm{l}\mathrm{o}{\mathrm{g}}_{4}3.\mathrm{l}\mathrm{o}{\mathrm{g}}_{3}x=2$​​ có​​ tất cả bao nhiêu nghiệm?

 A. 1. B. 2. C. 3. D.​​ 0.

Câu​​ 51.​​ Biết​​ rằng​​ phương trình​​ $2\mathrm{l}\mathrm{o}\mathrm{g}\left(x+2\right)+\mathrm{l}\mathrm{o}\mathrm{g}4=\mathrm{l}\mathrm{o}\mathrm{g}x+4\mathrm{l}\mathrm{o}\mathrm{g}3$​​ có hai nghiệm​​ phân biệt​​ $x_1,x_2\mathrm{ }\mathrm{ }\left(x_1<x_2\right)$. Tính​​ $P=\frac{x_1}{x_2}.$

 A.​​ $P=4.$ B.​​ $P=\frac{1}{4}.$ C.​​ $P=64.$ D.​​ $P=\frac{1}{64}.$

Câu​​ 52.​​ Biết​​ rằng​​ phương trình​​ ${\left[\mathrm{l}\mathrm{o}{\mathrm{g}}_{\frac{1}{3}}\left(9x\right)\right]}^2+\mathrm{l}\mathrm{o}{\mathrm{g}}_3\frac{x^2}{81}-7=0$​​ có hai nghiệm​​ phân biệt​​ $x_1,x_2$. Tính​​ $P=x_1{x}_2.$

 A.​​ $P=\frac{1}{9^3}.$ B.​​ $P=3^6.$ C.​​ $P=9^3.$ D.​​ $P=3^8.$

Câu 53. (ĐỀ CHÍNH THỨC 2016 – 2017)​​ Tìm tập nghiệm​​ $S$​​ của phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_{\sqrt{2}}\left(x-1\right)+\mathrm{l}\mathrm{o}{\mathrm{g}}_{\frac{1}{2}}\left(x+1\right)=1.$

 A.​​ $\mathit{S}=\left\{\frac{3+\sqrt{13}}{2}\right\}.$  B.​​ $\mathit{S}=\left\{3\right\}.$ 

 C.​​ $\mathit{S}=\left\{2-\sqrt{5};2+\sqrt{5}\right\}.$ D.​​ $\mathit{S}=\left\{2+\sqrt{5}\right\}.$

Câu 54.​​ Cho phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left[\mathrm{l}\mathrm{o}{\mathrm{g}}_{\frac{1}{8}}\left(x^3\right)+\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x+x+1\right]=3.$​​ Mệnh đề nào sau đây là đúng?

 A. Nghiệm của phương trình là số nguyên âm.

 B. Nghiệm của phương trình là số chính phương.

 C. Nghiệm của phương trình là số nguyên tố.​​  

 D. Nghiệm của phương trình là số vô tỉ.

Câu​​ 55.​​ Số nghiệm của phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_4\left(\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x\right)+\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(\mathrm{l}\mathrm{o}{\mathrm{g}}_{4}x\right)=2$​​ là:

 A. 0.​​  B. 1.​​  C. 2.​​  D. Nhiều hơn​​ $2$.

Câu 56.​​ Tính​​ $P$​​ tích tất cả các nghiệm của phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x-\mathrm{l}\mathrm{o}{\mathrm{g}}_{x}64=1.$

 A.​​ $P=1$.​​  B.​​ $P=2$.​​  C.​​ $P=4$.​​  D.​​ $P=8$.

Câu​​ 57.​​ Tìm tập nghiệm​​ $S$​​ của phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(9-2^x\right)=3-x.$​​ 

 A.​​ $S=\left\{-3;0\right\}.$​​  B.​​ $S=\left\{0;3\right\}.$ C.​​ $S=\left\{1;3\right\}.$ D.​​ $S=\left\{-3;1\right\}.$

Câu 58.​​ Biết rằng phương trình​​ $\mathrm{l}\mathrm{o}\mathrm{g}x.\mathrm{l}\mathrm{o}\mathrm{g}\left(100x^2\right)=4$​​ có hai nghiệm có dạng​​ $x_1$​​ và​​ $\frac{1}{x_2}$​​ trong đó​​ $x_1,x_2$​​ là những số nguyên. Mệnh đề nào sau đây là đúng?

 A.​​ $x_2=\frac{1}{x_1^2}$.​​  B.​​ $x_2=x_1^2$.​​  C.​​ $x_1.x_2=1$.​​  D.​​ $x_2=100x_1$.​​ 

Câu 59.​​ Phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_{2017}x+\mathrm{l}\mathrm{o}{\mathrm{g}}_{2016}x=0$​​ có tất cả bao nhiêu nghiệm?

 A.​​ 0. B.​​ 1. C.​​ 2. D.​​ 3.

Câu 60.​​ Cho phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_{4}x.\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(4x\right)+\mathrm{l}\mathrm{o}{\mathrm{g}}_{\sqrt{2}}\left(\frac{x^3}{2}\right)=0$. Nếu đặt​​ $t=\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x,$​​ ta được phương trình nào sau đây?

 A.​​ $t^2+14t-4=0.$ B.​​ $t^2+11t-3=0.$ 

 C.​​ $t^2+14t-2=0.$ D.​​ $t^2+11t-2=0.$

Câu 61.​​ Tổng lập phương các nghiệm của phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x.\mathrm{l}\mathrm{o}{\mathrm{g}}_3\left(2x-1\right)=2\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x$​​ bằng:

 A.​​ $6$.​​  B.​​ $26$.​​  C.​​ $126$.​​  D.​​ $216$.

Câu 62.​​ Biết rằng phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_3\left(3^{x+1}-1\right)=2x+\mathrm{l}\mathrm{o}{\mathrm{g}}_{\frac{1}{3}}2$​​ có hai nghiệm​​ $x_1$​​ và​​ $x_2.$​​ Hãy tính tổng​​ $S=27^{x_1}+27^{x_2}.$​​ 

 A.​​ $S=180.$​​  B.​​ $S=45.$​​  C.​​ $S=9.$​​  D.​​ $S=252.$​​ 

Câu 63.​​ Số nghiệm của phương trình​​ $\frac{x^3-5x^2+6x}{\mathrm{l}\mathrm{n}\left(x-1\right)}=0$​​ là:

 A. 0.​​  B. 1.​​  C. 2. C. 3.

Câu 64.​​ Biết rằng phương trình​​ $2\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x+\mathrm{l}\mathrm{o}{\mathrm{g}}_{\frac{1}{2}}\left(1-\sqrt{x}\right)=\frac{1}{2}\mathrm{l}\mathrm{o}{\mathrm{g}}_{\sqrt{2}}\left(x-2\sqrt{x}+2\right)$​​ có nghiệm duy nhất có dạng​​ $a+b\sqrt{3}$​​ với​​ $a,b\in \mathbb{Z}$. Tính tổng​​ $S=a+b.$

 A.​​ $S=6.$ ​​​​  B.​​ $S=2.$ ​​​​  C.​​ $S=-2.$ ​​​​  D.​​ $S=-6.$ ​​​​ 

Câu 65.​​ Phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_3\frac{x^2-2x+1}{x}+x^2+1=3x$​​ có tổng tất cả các nghiệm bằng:​​ 

 A.​​ 3.​​  B.​​ 5. C.​​ $\sqrt{5}$. ​​  D.​​ 2.

Câu 66. (ĐỀ MINH HỌA 2016 – 2017)​​ Giải bất phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(3x-1\right)>3$.​​ 

 A.​​ $x>3$.​​  B.​​ $\frac{1}{3}<x<3$. C.​​ $x<3$.​​  D.​​ $x>\frac{10}{3}$.

Câu​​ 67.​​ Cho bất phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_{\frac{1}{3}}\left(x^2-2x+6\right)\le -2$. Mệnh đề nào sau đây là đúng?

 A.​​ Tập nghiệm của bất phương trình​​ là nửa khoảng.  

 B.​​ Tập nghiệm của bất phương trình​​ là một đoạn.

 C.​​ Tập nghiệm của bất phương trình​​ là hợp của hai nửa khoảng.​​ 

 D.​​ Tập nghiệm của bất phương trình​​ là hợp của hai đoạn.

Câu 68.​​ Gọi​​ $M\left(x_0;y_0\right)$​​ là điểm thuộc đồ thị hàm số​​ $y=\mathrm{l}\mathrm{o}{\mathrm{g}}_{3}x$. Tìm điều kiện của​​ $x_0$​​ để điểm​​ $M$​​ nằm phía trên đường thẳng​​ $y=2$.

 A.​​ $x_0>0$.​​  B.​​ $x_0>9$.​​  C.​​ $x_0>2$.​​  D.​​ $x_0<2$.

Câu 69.​​ Tìm tập nghiệm​​ $S$​​ của bất phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_{\frac{1}{5}}\left(x^2-1\right)<\mathrm{l}\mathrm{o}{\mathrm{g}}_{\frac{1}{5}}\left(3x-3\right).$

 A.​​ $S=\left(2;+\mathrm{\infty }\right).$  B.​​ $S=\left(-\mathrm{\infty };1\right)\cup \left(2;+\mathrm{\infty }\right).$

 C.​​ $S=\left(-\mathrm{\infty };-1\right)\cup \left(2;+\mathrm{\infty }\right).$ D.​​ $S=\left(1;2\right).$

Câu 70.​​ Tìm tập nghiệm​​ $S$​​ của bất phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_a\left(x^2-x-2\right)>\mathrm{l}\mathrm{o}{\mathrm{g}}_a\left(-x^2+2x+3\right)$, biết​​ $\frac{9}{4}$​​ thuộc​​ $S.$

 A.​​ $S=\left(2;\frac{5}{2}\right)$. B.​​ $S=\left(-1;\frac{5}{2}\right)$.​​  C.​​ $S=\left(-\mathrm{\infty };-1\right)$. D.​​ $S=\left(\frac{5}{2};+\mathrm{\infty }\right)$.

Câu​​ 71.​​ Tìm tập nghiệm​​ $S$​​ của bất phương trình​​ $\mathrm{l}\mathrm{n}{x}^2>\mathrm{l}\mathrm{n}\left(4x-4\right).$

 A.​​ $S=\left(2;+\mathrm{\infty }\right)$.​​  B.​​ $S=\left(1;+\mathrm{\infty }\right)$.​​  C.​​ $S=\mathbb{R}\backslash \left\{2\right\}$. D.​​ $S=\left(1;+\mathrm{\infty }\right)\backslash \left\{2\right\}.$

Câu​​ 72.​​ Gọi​​ $S$​​ là tập nghiệm của bất phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_{\mathrm{0,3}}\left(4x^2\right)\ge \mathrm{l}\mathrm{o}{\mathrm{g}}_{\mathrm{0,3}}\left(12x-5\right).$​​ Kí hiệu​​ $m,M$​​ lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của tập​​ $S$. Mệnh đề nào sau đây là đúng?

 A.​​ $m+M=3.$​​  B.​​ $m+M=2$.​​  C.​​ $M-m=3.$​​  D.​​ $M-m=1.$​​ 

Câu​​ 73.​​ Tìm tập nghiệm​​ $S$​​ của bất phương trình​​ $\mathrm{l}\mathrm{o}\mathrm{g}10^{\mathrm{l}\mathrm{o}\mathrm{g}\left(x^2+21\right)}<1+\mathrm{l}\mathrm{o}\mathrm{g}x.$

 A.​​ $S=\left(3;7\right).$  B.​​ $S=\left(-\mathrm{\infty };3\right)\cup \left(7;+\mathrm{\infty }\right).$

 C.​​ $S=\left(-\mathrm{\infty };3\right).$  D.​​ $S=\left(7;+\mathrm{\infty }\right).$

Câu 74.​​ Có bao nhiêu số nguyên dương​​ $x$​​ thỏa mãn bất phương trình​​ $\mathrm{l}\mathrm{o}\mathrm{g}\left(x-40\right)+\mathrm{l}\mathrm{o}\mathrm{g}\left(60-x\right)<2$?

 A.​​ 20. B.​​ 18. C.​​ 21. D.​​ 19.

Câu​​ 75.​​ Biết rằng tập nghiệm của bất phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(1+\mathrm{l}\mathrm{o}{\mathrm{g}}_{\frac{1}{9}}x-\mathrm{l}\mathrm{o}{\mathrm{g}}_{9}x\right)<1$​​ có dạng​​ $S=\left(\frac{1}{a};b\right)$​​ với​​ $a,b$​​ là những số nguyên. Mệnh đề nào sau đây là đúng?

 ​​ A.​​ $a=-b$.​​  B.​​ $a+b=1$.​​  C.​​ $a=b$.​​  D.​​ $a=2b$.​​ 

Câu​​ 76.​​ Có bao nhiêu giá trị nguyên của​​ $x$​​ trong đoạn​​ $\left[-2018;2018\right]$​​ thỏa mãn bất phương trình​​ $\mathrm{l}\mathrm{o}\mathrm{g}{}_{\frac{\pi }{4}}{}^{\mathrm{ }}\mathrm{ }\left[\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(x+\sqrt{2x^2-x}\right)\right]<0?$

 A.​​ $4033.$ B.​​ $4031.$ C.​​ $4037.$ D.​​ $2018.$

Câu​​ 77.​​ Tìm tập nghiệm​​ $S$​​ của bất phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x+\mathrm{l}\mathrm{o}{\mathrm{g}}_{3}x>1+\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x\mathrm{l}\mathrm{o}{\mathrm{g}}_{3}x.$

 A.​​ $S=\left(3;+\mathrm{\infty }\right).$  B.​​ $S=\left(0;2\right)\cup \left(3;+\mathrm{\infty }\right).$ 

 C.​​ $S=\left(2;3\right).$  D.​​ $S=\left(-\mathrm{\infty };2\right)\cup \left(3;+\mathrm{\infty }\right).$

Câu​​ 78.​​ Có tất cả bao nhiêu số nguyên thỏa mãn bất phương trình​​ $\mathrm{l}\mathrm{o}\mathrm{g}{}_{\frac{1}{2}}{}^{\mathrm{ }}\mathrm{ }\left[\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(2-x^2\right)\right]>0$?

 ​​ A.​​ $1$.​​  B.​​ $2$.​​  C.​​ $3$.​​  D.​​ $0$.​​ 

Câu 79.​​ Tìm tập nghiệm​​ $S$​​ của bất phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_{\frac{1}{2}}\left(\mathrm{l}\mathrm{o}{\mathrm{g}}_3\frac{2x+1}{x-1}\right)>0.$

 ​​ ​​ ​​ ​​​​  A.​​ $S=\left(-\mathrm{\infty };1\right)\cup \left(4;+\mathrm{\infty }\right).$ B.​​ $S=\left(-\mathrm{\infty };-2\right)\cup \left(1;+\mathrm{\infty }\right).$​​   ​​​​  

 C.​​ $S=\left(-2;1\right)\cup \left(1;4\right).$​​  D.​​ $S=\left(-\mathrm{\infty };-2\right)\cup \left(4;+\mathrm{\infty }\right).$

Câu​​ 80.​​ Tìm tập nghiệm​​ $S$​​ của bất phương trình​​ $\frac{1-\mathrm{l}\mathrm{o}{\mathrm{g}}_{4}x}{1-\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x}\le \frac{1}{2}.$

 A.​​ $S=\left(0;2\right).$​​  B.​​ $S=\left[2;+\mathrm{\infty }\right).$ C.​​ $S=\left(-\mathrm{\infty };2\right).$ D.​​ $S=\left(2;+\mathrm{\infty }\right).$

 

C.Đáp án và lời giải

Câu 46. (ĐỀ MINH HỌA 2016 – 2017)​​ Giải phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_4\left(x-1\right)=3$.

 A.​​ $x=63$.​​  B.​​ $x=65$.​​  C.​​ $x=80$.​​  D.​​ $x=82$.

Lời giải.​​ Phương trình​​ $\iff x-1=4^3\iff x-1=64\iff x=65.$​​ Chọn B.

Câu​​ 47.​​ Tìm tập nghiệm​​ $S$​​ của phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_6\left[x\left(5-x\right)\right]=1.$

 A.​​ $S=\left\{2;3\right\}.$ B.​​ $S=\left\{4;6\right\}$.​​  C.​​ $S=\left\{1;-6\right\}$.​​  D.​​ $S=\left\{-1;6\right\}$.

Lời giải.​​ Phương trình​​ $\iff x\left(5-x\right)=6\iff x^2-5x+6=0\iff \left[\begin{array}{l}x=2\\ x=3\end{array}\right..$​​ Chọn A.

Câu​​ 48.​​ Phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(x-3\sqrt{x}+4\right)=3$​​ có tất cả bao nhiêu nghiệm?

 A.​​ 4.​​  B. 1.​​  C. 2.​​  D.​​ 0.

Lời giải.​​ Phương trình​​ $\iff x-3\sqrt{x}+4=8\iff x-3\sqrt{x}-4=0$

$\iff \left[\begin{array}{l}\sqrt{x}=-1\left(\mathrm{v}\mathrm{o}\mathrm{n}\mathrm{g}\mathrm{h}\mathrm{i}\mathrm{e}\mathrm{m}\right)\\ \sqrt{x}=4\end{array}\right.\iff x=16.$​​ Chọn B.

Câu​​ 49.​​ Tính​​ $P$​​ là tích tất cả các nghiệm của phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_{\frac{1}{2}}\frac{x^2-3x+2}{x}=0.$

 A.​​ $P=4.$​​  B.​​ $P=2\sqrt{2}.$ C.​​ $P=2.$​​  D.​​ $P=1.$

Lời giải.​​ Phương trình​​ $\iff \frac{x^2-3x+2}{x}=1\iff x^2-4x+2=0$

$$\iff \left[\begin{array}{l}x=2-\sqrt{2}=x_1\\ x=2+\sqrt{2}=x_2\end{array}\right.$$

$\stackrel{}{\to }P=x_1{x}_2=\left(2-\sqrt{2}\right)\left(2+\sqrt{2}\right)=4-2=2.$​​ Chọn C.

Hoặc từ phương trình​​ $x^2-4x+2=0\stackrel{\mathrm{V}\mathrm{i}\mathrm{e}\mathrm{t}}{\to }{x}_1{x}_2=2.$

Câu​​ 50.​​ Phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(x-3\right)+2\mathrm{l}\mathrm{o}{\mathrm{g}}_{4}3.\mathrm{l}\mathrm{o}{\mathrm{g}}_{3}x=2$​​ có​​ tất cả bao nhiêu nghiệm?

 A. 1. B. 2. C. 3. D.​​ 0.

Lời giải.​​ Điều kiện:​​ $\left\{\begin{array}{l}x-3>0\\ x>0\end{array}\right.\iff x>3.$

Phương trình​​ $\iff \mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(x-3\right)+2\mathrm{l}\mathrm{o}{\mathrm{g}}_{4}x=2\iff \mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(x-3\right)+\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x=2$

$$\iff \mathrm{l}\mathrm{o}{\mathrm{g}}_2\left[\left(x-3\right)x\right]=2\iff \left(x-3\right)x=2^2$$

$\iff x^2-3x-4=0\iff \left[\begin{array}{l}x=-1\left(\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{ï}\mathrm{i}\right)\\ x=4\left(\mathrm{t}\mathrm{h}\mathrm{o}\mathrm{a}\mathrm{û}\mathrm{m}\mathrm{a}\mathrm{õ}\mathrm{n}\right)\end{array}\right.$Chọn A.

Câu​​ 51.​​ Biết​​ rằng​​ phương trình​​ $2\mathrm{l}\mathrm{o}\mathrm{g}\left(x+2\right)+\mathrm{l}\mathrm{o}\mathrm{g}4=\mathrm{l}\mathrm{o}\mathrm{g}x+4\mathrm{l}\mathrm{o}\mathrm{g}3$​​ có hai nghiệm​​ phân biệt​​ $x_1,x_2\mathrm{ }\mathrm{ }\left(x_1<x_2\right)$. Tính​​ $P=\frac{x_1}{x_2}.$

 A.​​ $P=4.$ B.​​ $P=\frac{1}{4}.$ C.​​ $P=64.$ D.​​ $P=\frac{1}{64}.$

Lời giải.​​ Điều kiện:​​ $x>0.$

Phương trình​​ $\iff \mathrm{l}\mathrm{o}\mathrm{g}{\left(x+2\right)}^2+\mathrm{l}\mathrm{o}\mathrm{g}4=\mathrm{l}\mathrm{o}\mathrm{g}x+\mathrm{l}\mathrm{o}\mathrm{g}81$

$$\iff \mathrm{l}\mathrm{o}\mathrm{g}\left[4{\left(x+2\right)}^2\right]=\mathrm{l}\mathrm{o}\mathrm{g}\left(81x\right)$$

$$\iff 4{\left(x+2\right)}^2=81x\iff 4x^2-65x+16=0$$

$\iff \left[\begin{array}{l}x=\frac{1}{4}=x_1\left(\mathrm{t}\mathrm{h}\mathrm{o}\mathrm{û}\mathrm{a}\mathrm{m}\mathrm{a}\mathrm{õ}\mathrm{n}\right)\\ x=16=x_2\left(\mathrm{t}\mathrm{h}\mathrm{o}\mathrm{û}\mathrm{a}\mathrm{m}\mathrm{a}\mathrm{õ}\mathrm{n}\right)\end{array}\right.\stackrel{}{\to }P=\frac{x_1}{x_2}=\frac{1}{4.16}=\frac{1}{64}$Chọn D.

Câu​​ 52.​​ Biết​​ rằng​​ phương trình​​ ${\left[\mathrm{l}\mathrm{o}{\mathrm{g}}_{\frac{1}{3}}\left(9x\right)\right]}^2+\mathrm{l}\mathrm{o}{\mathrm{g}}_3\frac{x^2}{81}-7=0$​​ có hai nghiệm​​ phân biệt​​ $x_1,x_2$. Tính​​ $P=x_1{x}_2.$

 A.​​ $P=\frac{1}{9^3}.$ B.​​ $P=3^6.$ C.​​ $P=9^3.$ D.​​ $P=3^8.$

Lời giải.​​ Điều kiện:​​ $x>0$.

Phương trình​​ $\iff {\left(-2-\mathrm{l}\mathrm{o}{\mathrm{g}}_{3}x\right)}^2+\mathrm{l}\mathrm{o}{\mathrm{g}}_3{x}^2-\mathrm{l}\mathrm{o}{\mathrm{g}}_{3}81-7=0$

$$\iff \mathrm{l}\mathrm{o}{\mathrm{g}}_3^{2}x+6\mathrm{l}\mathrm{o}{\mathrm{g}}_{3}x-7=0\iff \left[\begin{array}{l}\mathrm{l}\mathrm{o}{\mathrm{g}}_{3}x=1\\ \mathrm{l}\mathrm{o}{\mathrm{g}}_{3}x=-7\end{array}\right.$$

$$\iff \left[\begin{array}{l}x=3=x_1\left(\mathrm{t}\mathrm{h}\mathrm{o}\mathrm{a}\right)\\ x=3^{-7}=x_2\left(\mathrm{t}\mathrm{h}\mathrm{o}\mathrm{a}\right)\end{array}\right.$$

$\stackrel{}{\to }P=x_1{x}_2=3.3^{-7}=3^{-6}=\frac{1}{3^6}=\frac{1}{9^3}.$​​ Chọn A.

Câu 53. (ĐỀ CHÍNH THỨC 2016 – 2017)​​ Tìm tập nghiệm​​ $S$​​ của phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_{\sqrt{2}}\left(x-1\right)+\mathrm{l}\mathrm{o}{\mathrm{g}}_{\frac{1}{2}}\left(x+1\right)=1.$

 A.​​ $\mathit{S}=\left\{\frac{3+\sqrt{13}}{2}\right\}.$  B.​​ $\mathit{S}=\left\{3\right\}.$ 

 C.​​ $\mathit{S}=\left\{2-\sqrt{5};2+\sqrt{5}\right\}.$ D.​​ $\mathit{S}=\left\{2+\sqrt{5}\right\}.$

Lời giải.​​ Điều kiện:​​ $x>1.$

Phương trình​​ $\iff 2\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(x-1\right)-\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(x+1\right)=1$

$$\iff \mathrm{l}\mathrm{o}{\mathrm{g}}_2{\left(x-1\right)}^2=1+\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(x+1\right)$$

$$\iff \mathrm{l}\mathrm{o}{\mathrm{g}}_2{\left(x-1\right)}^2=\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left[2\left(x+1\right)\right]$$

$$\iff {\left(x-1\right)}^2=2\left(x+1\right)$$

$$\iff x^2-4x-1=0\iff \left[\begin{array}{l}x=2+\sqrt{5}\left(\mathrm{t}\mathrm{h}\mathrm{o}\mathrm{a}\right)\\ x=2-\sqrt{5}\left(\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{i}\right)\end{array}\right.$$​​ 

$\stackrel{}{\to }S=\left\{2+\sqrt{5}\right\}$Chọn D.

Câu 54.​​ Cho phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left[\mathrm{l}\mathrm{o}{\mathrm{g}}_{\frac{1}{8}}\left(x^3\right)+\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x+x+1\right]=3.$​​ Mệnh đề nào sau đây là đúng?

 A. Nghiệm của phương trình là số nguyên âm.

 B. Nghiệm của phương trình là số chính phương.

 C. Nghiệm của phương trình là số nguyên tố.​​  

 D. Nghiệm của phương trình là số vô tỉ.

Lời giải.​​ Điều kiện:​​ $x>0.$

Phương trình​​ $\iff \mathrm{l}\mathrm{o}{\mathrm{g}}_2\left[-\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x+\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x+x+1\right]=3$

$\iff \mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(x+1\right)=3\iff x+1=8\iff x=7\left(\mathrm{t}\mathrm{h}\mathrm{o}\mathrm{û}\mathrm{a}\mathrm{m}\mathrm{a}\mathrm{õ}\mathrm{n}\right).$​​ Chọn C.

Câu​​ 55.​​ Số nghiệm của phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_4\left(\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x\right)+\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(\mathrm{l}\mathrm{o}{\mathrm{g}}_{4}x\right)=2$​​ là:

 A. 0.​​  B. 1.​​  C. 2.​​  D. Nhiều hơn​​ $2$.

Lời giải.​​ Điều kiện:​​ $\left\{\begin{array}{l}x>0\\ \mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x>0\\ \mathrm{l}\mathrm{o}{\mathrm{g}}_{4}x>0\end{array}\right.\iff x>1$.

Phương trình​​ $\iff \frac{1}{2}\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x\right)+\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(\frac{1}{2}\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x\right)=2$

$$\iff \frac{1}{2}\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x\right)+\mathrm{l}\mathrm{o}{\mathrm{g}}_2\frac{1}{2}+\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x\right)=2$$

$$\iff \frac{1}{2}\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x\right)-1+\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x\right)=2$$

$$\iff \frac{3}{2}\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x\right)=3\iff \mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x\right)=2$$

$\iff \mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x=4\iff x=16\left(\mathrm{t}\mathrm{h}\mathrm{o}\mathrm{a}\right).$​​ Vậy phương trình có nghiệm duy nhất.​​ Chọn B.

Câu 56.​​ Tính​​ $P$​​ tích tất cả các nghiệm của phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x-\mathrm{l}\mathrm{o}{\mathrm{g}}_{x}64=1.$

 A.​​ $P=1$.​​  B.​​ $P=2$.​​  C.​​ $P=4$.​​  D.​​ $P=8$.

Lời giải.​​ Điều kiện:​​ $0<x\ne 1$.

Phương trình​​ $\iff \mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x-6\mathrm{l}\mathrm{o}{\mathrm{g}}_{x}2=1.$

Đặt​​ $t=\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x\left(t\ne 0\right)$, phương trình trở thành​​ $t-\frac{6}{t}=1\iff \left\{\begin{array}{l}{t}^2-t-6=0\\ t\ne 0\end{array}\right.\iff \left[\begin{array}{l}t=3\\ t=-2\end{array}\right.$

$$\Rightarrow \left[\begin{array}{l}\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x=3\\ \mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x=-2\end{array}\right.\iff \left[\begin{array}{l}x=8=x_1\\ x=\frac{1}{4}=x_2\end{array}\right.$$​​ 

$\Rightarrow P=x_1{x}_2=2$Chọn B.

Câu​​ 57.​​ Tìm tập nghiệm​​ $S$​​ của phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(9-2^x\right)=3-x.$​​ 

 A.​​ $S=\left\{-3;0\right\}.$​​  B.​​ $S=\left\{0;3\right\}.$ C.​​ $S=\left\{1;3\right\}.$ D.​​ $S=\left\{-3;1\right\}.$

Lời giải.​​ Phương trình​​ $\iff 9-2^x=2^{3-x}\iff 9-2^x=\frac{8}{2^x}$

$\iff {\left(2^x\right)}^2-9.2^x+8=0\iff \left[\begin{array}{l}{2}^x=1\\ 2^x=8\end{array}\right.\iff \left[\begin{array}{l}x=0\\ x=3\end{array}\right..$​​ Chọn B.

Câu 58.​​ Biết rằng phương trình​​ $\mathrm{l}\mathrm{o}\mathrm{g}x.\mathrm{l}\mathrm{o}\mathrm{g}\left(100x^2\right)=4$​​ có hai nghiệm có dạng​​ $x_1$​​ và​​ $\frac{1}{x_2}$​​ trong đó​​ $x_1,x_2$​​ là những số nguyên. Mệnh đề nào sau đây là đúng?

 A.​​ $x_2=\frac{1}{x_1^2}$.​​  B.​​ $x_2=x_1^2$.​​  C.​​ $x_1.x_2=1$.​​  D.​​ $x_2=100x_1$.​​ 

Lời giải.​​ Điều kiện:​​ $x>0$.

Phương trình​​ $\iff \mathrm{l}\mathrm{o}\mathrm{g}x\left(\mathrm{l}\mathrm{o}\mathrm{g}100+\mathrm{l}\mathrm{o}\mathrm{g}{x}^2\right)=4\iff \mathrm{l}\mathrm{o}\mathrm{g}x\left(2+2\mathrm{l}\mathrm{o}\mathrm{g}x\right)=4$

$$\iff 2\mathrm{l}\mathrm{o}{\mathrm{g}}^{2}x+2\mathrm{l}\mathrm{o}\mathrm{g}x-4=0$$

$$\iff \left[\begin{array}{l}\mathrm{l}\mathrm{o}\mathrm{g}x=1\\ \mathrm{l}\mathrm{o}\mathrm{g}x=-2\end{array}\right.\iff \left[\begin{array}{l}x=10\left(\mathrm{t}\mathrm{h}\mathrm{o}\mathrm{a}\right)\\ x=\frac{1}{100}\left(\mathrm{t}\mathrm{h}\mathrm{o}\mathrm{a}\right)\end{array}\right.$$

Suy ra​​ $x_1=10$​​ và​​ $x_2=100$​​ nên​​ $x_2=x_1^2$.​​ Chọn B.

Câu 59.​​ Phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_{2017}x+\mathrm{l}\mathrm{o}{\mathrm{g}}_{2016}x=0$​​ có tất cả bao nhiêu nghiệm?

 A.​​ 0. B.​​ 1. C.​​ 2. D.​​ 3.

Lời giải.​​ Điều kiện:​​ $x>0$.

Phương trình​​ $\iff \mathrm{l}\mathrm{o}{\mathrm{g}}_{2017}x+\mathrm{l}\mathrm{o}{\mathrm{g}}_{2016}2017.\mathrm{l}\mathrm{o}{\mathrm{g}}_{2017}x=0$

$$\iff \mathrm{l}\mathrm{o}{\mathrm{g}}_{2017}x.\left(1+\mathrm{l}\mathrm{o}{\mathrm{g}}_{2016}2017\right)=0$$

$\iff \mathrm{l}\mathrm{o}{\mathrm{g}}_{2017}x=0\stackrel{}{\leftrightarrow }x=1.$​​ Chọn B.

Câu 60.​​ Cho phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_{4}x.\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(4x\right)+\mathrm{l}\mathrm{o}{\mathrm{g}}_{\sqrt{2}}\left(\frac{x^3}{2}\right)=0$. Nếu đặt​​ $t=\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x,$​​ ta được phương trình nào sau đây?

 A.​​ $t^2+14t-4=0.$ B.​​ $t^2+11t-3=0.$ 

 C.​​ $t^2+14t-2=0.$ D.​​ $t^2+11t-2=0.$

Lời giải.​​ Ta có​​ 

$$\mathrm{*}\mathrm{l}\mathrm{o}{\mathrm{g}}_{4}x.\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(4x\right)=\mathrm{l}\mathrm{o}{\mathrm{g}}_{2^2}x.\left(2+\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x\right)$$

$$=\frac{1}{2}\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x\left(2+\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x\right)=t+\frac{1}{2}{t}^2$$

$$\mathrm{*}\mathrm{l}\mathrm{o}{\mathrm{g}}_{\sqrt{2}}\left(\frac{x^3}{2}\right)=\mathrm{l}\mathrm{o}{\mathrm{g}}_{2^{\frac{1}{2}}}\left(\frac{x^3}{2}\right)=2\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(\frac{x^3}{2}\right)$$

$$=2\left(\mathrm{l}\mathrm{o}{\mathrm{g}}_2{x}^3-1\right)=6\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x-2=6t-2$$

Do đó phương trình đã cho trở thành​​ $t+\frac{1}{2}{t}^2+6t-2=0\iff t^2+14t-4=0$.​​ Chọn A.

Câu 61.​​ Tổng lập phương các nghiệm của phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x.\mathrm{l}\mathrm{o}{\mathrm{g}}_3\left(2x-1\right)=2\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x$​​ bằng:

 A.​​ $6$.​​  B.​​ $26$.​​  C.​​ $126$.​​  D.​​ $216$.

Lời giải.​​ Điều kiện:​​ $x>\frac{1}{2}$.

Phương trình​​ $\iff \mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x.\left[\mathrm{l}\mathrm{o}{\mathrm{g}}_3\left(2x-1\right)-2\right]=0$

$$\iff \left[\begin{array}{l}\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x=0\\ \mathrm{l}\mathrm{o}{\mathrm{g}}_3\left(2x-1\right)=2\end{array}\right.\iff \left[\begin{array}{l}x=1\\ 2x-1=9\end{array}\right.$$

$\iff \left[\begin{array}{l}x=1\left(\mathrm{t}\mathrm{h}\mathrm{o}\mathrm{a}\right)\\ x=5\left(\mathrm{t}\mathrm{h}\mathrm{o}\mathrm{a}\right)\end{array}\right.\stackrel{}{\to }{1}^3+5^3=126.$​​ Chọn C.​​ 

Câu 62.​​ Biết rằng phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_3\left(3^{x+1}-1\right)=2x+\mathrm{l}\mathrm{o}{\mathrm{g}}_{\frac{1}{3}}2$​​ có hai nghiệm​​ $x_1$​​ và​​ $x_2.$​​ Hãy tính tổng​​ $S=27^{x_1}+27^{x_2}.$​​ 

 A.​​ $S=180.$​​  B.​​ $S=45.$​​  C.​​ $S=9.$​​  D.​​ $S=252.$​​ 

Lời giải.​​ Điều kiện:​​ $3^{x+1}-1>0\iff x>-1.$

Phương trình​​ $\iff \mathrm{l}\mathrm{o}{\mathrm{g}}_3\left(3^{x+1}-1\right)=2x-\mathrm{l}\mathrm{o}{\mathrm{g}}_{3}2$

$$\iff \mathrm{l}\mathrm{o}{\mathrm{g}}_3\left(3^{x+1}-1\right)+\mathrm{l}\mathrm{o}{\mathrm{g}}_{3}2=2x$$

$$\iff \mathrm{l}\mathrm{o}{\mathrm{g}}_3\left[\left(3^{x+1}-1\right).2\right]=2x$$

$$\iff \left(3^{x+1}-1\right).2=3^{2x}\iff 6.3^x-2=3^{2x}$$

$$\iff 3^{2x}-6.3^x+2=0\stackrel{\mathrm{V}\mathrm{i}\mathrm{e}\mathrm{t}}{\to }\left\{\begin{array}{l}{3}^{x_1}+3^{x_2}=6\\ 3^{x_1}.3^{x_2}=2\end{array}\right..$$

Ta có​​ $S=27^{x_1}+27^{x_2}$​​ 

$$={\left(3^{x_1}+3^{x_2}\right)}^3-3.3^{x_1}.3^{x_2}\left(3^{x_1}+3^{x_2}\right)$$

$=6^3-3.2.6=180$Chọn A.

Câu 63.​​ Số nghiệm của phương trình​​ $\frac{x^3-5x^2+6x}{\mathrm{l}\mathrm{n}\left(x-1\right)}=0$​​ là:

 A. 0.​​  B. 1.​​  C. 2. C. 3.

Lời giải.​​ Điều kiện:​​ $\left\{\begin{array}{l}x-1>0\\ \mathrm{l}\mathrm{n}\left(x-1\right)\ne 0\end{array}\right.\iff \left\{\begin{array}{l}x>1\\ x\ne 2\end{array}\right.$.

Phương trình​​ $\iff x^3-5x^2+6x=0\iff \left[\begin{array}{l}x=0\\ x=2\\ x=3\end{array}\right..$

Đối chiếu với điều kiện, phương trình có nghiệm duy nhất​​ $x=3$.​​ Chọn B.

Câu 64.​​ Biết rằng phương trình​​ $2\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x+\mathrm{l}\mathrm{o}{\mathrm{g}}_{\frac{1}{2}}\left(1-\sqrt{x}\right)=\frac{1}{2}\mathrm{l}\mathrm{o}{\mathrm{g}}_{\sqrt{2}}\left(x-2\sqrt{x}+2\right)$​​ có nghiệm duy nhất có dạng​​ $a+b\sqrt{3}$​​ với​​ $a,b\in \mathbb{Z}$. Tính tổng​​ $S=a+b.$

 A.​​ $S=6.$ ​​​​  B.​​ $S=2.$ ​​​​  C.​​ $S=-2.$ ​​​​  D.​​ $S=-6.$ ​​​​ 

Lời giải.​​ Điều kiện:​​ $0<x<1$.

Phương trình​​ $\iff \mathrm{l}\mathrm{o}{\mathrm{g}}_2{x}^2-\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(1-\sqrt{x}\right)=\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(x-2\sqrt{x}+2\right)$

$$\iff \mathrm{l}\mathrm{o}{\mathrm{g}}_2\frac{x^2}{1-\sqrt{x}}=\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(x-2\sqrt{x}+2\right)$$​​ 

$$\iff \frac{x^2}{1-\sqrt{x}}=x-2\sqrt{x}+2$$

$$\iff \frac{x^2}{1-\sqrt{x}}=x+2\left(1-\sqrt{x}\right)$$

$$\iff \frac{x^2}{{\left(1-\sqrt{x}\right)}^2}=\frac{x}{1-\sqrt{x}}+2$$

$$\iff {\left(\frac{x}{1-\sqrt{x}}\right)}^2-\left(\frac{x}{1-\sqrt{x}}\right)-2=0$$

$\iff \frac{x}{1-\sqrt{x}}=-1$​​ (vô nghiệm) hoặc​​ $\frac{x}{1-\sqrt{x}}=2$

$$\iff x+2\sqrt{x}-2=0\Rightarrow \sqrt{x}=-1+\sqrt{3}$$​​ 

$$\Rightarrow x=4-2\sqrt{3}\Rightarrow \left\{\begin{array}{l}a=4\\ b=-2\end{array}\right.$$

Chọn B.

 

Câu 65.​​ Phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_3\frac{x^2-2x+1}{x}+x^2+1=3x$​​ có tổng tất cả các nghiệm bằng:​​ 

 A.​​ 3.​​  B.​​ 5. C.​​ $\sqrt{5}$. ​​  D.​​ 2.

Lời giải.​​ Điều kiện:​​ $\frac{x^2-2x+1}{x}>0\iff \frac{{\left(x-1\right)}^2}{x}>0\iff 0<x\ne 1.$

Phương trình​​ $\iff \mathrm{l}\mathrm{o}{\mathrm{g}}_3\frac{{\left(x-1\right)}^2}{x}+x^2-2x+1=x$

$$\iff \mathrm{l}\mathrm{o}{\mathrm{g}}_3{\left(x-1\right)}^2-\mathrm{l}\mathrm{o}{\mathrm{g}}_{3}x+{\left(x-1\right)}^2=x$$ 

$$\iff \mathrm{l}\mathrm{o}{\mathrm{g}}_3{\left(x-1\right)}^2+{\left(x-1\right)}^2=\mathrm{l}\mathrm{o}{\mathrm{g}}_{3}x+x$$ $$\left(\mathrm{*}\right)$$​​ 

Xét hàm số​​ $f\left(t\right)=\mathrm{l}\mathrm{o}{\mathrm{g}}_{3}t+t$​​ với​​ $t>0$. Ta có​​ $f\mathrm{\text{'}}\left(t\right)=\frac{1}{t\mathrm{l}\mathrm{n}3}+1>0,\forall t>0$.

Suy ra hàm số​​ $f\left(t\right)$​​ đồng biến trên​​ $\left(0;+\mathrm{\infty }\right).$

Nhận thấy​​ $\left(\mathrm{*}\right)$​​ có dạng​​ $f\left[{\left(x-1\right)}^2\right]=f\left(x\right)\mathrm{ }\iff {\left(x-1\right)}^2=x$

$\iff x^2-3x+1=0\iff \left[\begin{array}{l}x=\frac{3+\sqrt{5}}{2}\left(\mathrm{t}\mathrm{h}\mathrm{o}\mathrm{a}\right)\\ x=\frac{3-\sqrt{5}}{2}\left(\mathrm{t}\mathrm{h}\mathrm{o}\mathrm{a}\right)\end{array}\right.\stackrel{}{\to }\frac{3+\sqrt{5}}{2}+\frac{3-\sqrt{5}}{2}=3.$​​ Chọn A.

Câu 66. (ĐỀ MINH HỌA 2016 – 2017)​​ Giải bất phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(3x-1\right)>3$.​​ 

 A.​​ $x>3$.​​  B.​​ $\frac{1}{3}<x<3$. C.​​ $x<3$.​​  D.​​ $x>\frac{10}{3}$.

Lời giải.​​ Bất phương trình​​ $\iff 3x-1>2^3\iff 3x>9\iff x>3.$​​ Chọn A.

Câu​​ 67.​​ Cho bất phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_{\frac{1}{3}}\left(x^2-2x+6\right)\le -2$. Mệnh đề nào sau đây là đúng?

 A.​​ Tập nghiệm của bất phương trình​​ là nửa khoảng.  

 B.​​ Tập nghiệm của bất phương trình​​ là một đoạn.

 C.​​ Tập nghiệm của bất phương trình​​ là hợp của hai nửa khoảng.​​ 

 D.​​ Tập nghiệm của bất phương trình​​ là hợp của hai đoạn.

Lời giải.​​ Bất phương trình​​ $\iff -\mathrm{l}\mathrm{o}{\mathrm{g}}_3\left(x^2-2x+6\right)\le -2\iff \mathrm{l}\mathrm{o}{\mathrm{g}}_3\left(x^2-2x+6\right)\ge 2$

$$\iff x^2-2x+6\ge 9\iff x^2-2x-3\ge 0\iff \left[\begin{array}{l}x\ge 3\\ x\le -1\end{array}\right..$$

Vậy bất phương trình có tập nghiệm là​​ $S=\left(-\mathrm{\infty };-1\right]\cup \left[3;+\mathrm{\infty }\right)$.​​ Chọn C.

Câu 68.​​ Gọi​​ $M\left(x_0;y_0\right)$​​ là điểm thuộc đồ thị hàm số​​ $y=\mathrm{l}\mathrm{o}{\mathrm{g}}_{3}x$. Tìm điều kiện của​​ $x_0$​​ để điểm​​ $M$​​ nằm phía trên đường thẳng​​ $y=2$.

 A.​​ $x_0>0$.​​  B.​​ $x_0>9$.​​  C.​​ $x_0>2$.​​  D.​​ $x_0<2$.

Lời giải.​​ Đồ thị​​ $y=\mathrm{l}\mathrm{o}{\mathrm{g}}_{3}x$​​ nằm ở phía trên đường thẳng​​ $y=2$​​ khi​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_{3}x>2\iff x>9$.

Chọn B.

Câu 69.​​ Tìm tập nghiệm​​ $S$​​ của bất phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_{\frac{1}{5}}\left(x^2-1\right)<\mathrm{l}\mathrm{o}{\mathrm{g}}_{\frac{1}{5}}\left(3x-3\right).$

 A.​​ $S=\left(2;+\mathrm{\infty }\right).$  B.​​ $S=\left(-\mathrm{\infty };1\right)\cup \left(2;+\mathrm{\infty }\right).$

 C.​​ $S=\left(-\mathrm{\infty };-1\right)\cup \left(2;+\mathrm{\infty }\right).$ D.​​ $S=\left(1;2\right).$

Lời giải.​​ Điều kiện:​​ $\left\{\begin{array}{l}{x}^2-1>0\\ 3x-3>0\end{array}\right.\iff x>1.$

Bất phương trình:​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_{\frac{1}{5}}\left(x^2-1\right)<\mathrm{l}\mathrm{o}{\mathrm{g}}_{\frac{1}{5}}\left(3x-3\right)\iff x^2-1>3x-3$(chú ý với cơ số​​ $\frac{1}{5}<1$)

$\iff x^2-3x+2>0\iff \left[\begin{array}{l}x>2\\ x<1\end{array}\right.\stackrel{\mathrm{d}\mathrm{k}:x>1}{\to }x>2.$​​ Chọn A.

Câu 70.​​ Tìm tập nghiệm​​ $S$​​ của bất phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_a\left(x^2-x-2\right)>\mathrm{l}\mathrm{o}{\mathrm{g}}_a\left(-x^2+2x+3\right)$, biết​​ $\frac{9}{4}$​​ thuộc​​ $S.$

 A.​​ $S=\left(2;\frac{5}{2}\right)$. B.​​ $S=\left(-1;\frac{5}{2}\right)$.​​  C.​​ $S=\left(-\mathrm{\infty };-1\right)$. D.​​ $S=\left(\frac{5}{2};+\mathrm{\infty }\right)$.

Lời giải.​​ Điều kiện:​​ $\left\{\begin{array}{l}{x}^2-x-2>0\\ -x^2+2x+3>0\\ 0<a\ne 1\end{array}\right.\iff \left\{\begin{array}{l}2<x<3\\ 0<a\ne 1\end{array}\right..$

Do​​ $x=\frac{9}{4}$​​ là nghiệm của bất phương trình đã cho nên​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_a\frac{13}{16}>\mathrm{l}\mathrm{o}{\mathrm{g}}_a\frac{39}{16}\stackrel{}{\to }0<a<1.$

Vì​​ $0<a<1$​​ nên bất phương trình​​ $\iff x^2-x-2<-x^2+2x+3$

$$\iff 2x^2-3x-5<0$$​​ 

$\iff -1<x<\frac{5}{2}\stackrel{\mathrm{d}\mathrm{k}:2<x<3}{\to }2<x<\frac{5}{2}$Chọn A.

Câu​​ 71.​​ Tìm tập nghiệm​​ $S$​​ của bất phương trình​​ $\mathrm{l}\mathrm{n}{x}^2>\mathrm{l}\mathrm{n}\left(4x-4\right).$

 A.​​ $S=\left(2;+\mathrm{\infty }\right)$.​​  B.​​ $S=\left(1;+\mathrm{\infty }\right)$.​​  C.​​ $S=\mathbb{R}\backslash \left\{2\right\}$. D.​​ $S=\left(1;+\mathrm{\infty }\right)\backslash \left\{2\right\}.$

Lời giải.​​ Điều kiện:​​ $\left\{\begin{array}{l}4x-4>0\\ x\ne 0\end{array}\right.\iff x>1.$

Bất phương trình​​ $\iff x^2>4x-4\iff x^2-4x+4>0$

$\iff {\left(x-2\right)}^2>0\iff x\ne 2$.

Đối chiếu điều kiện, ta được tập nghiệm của bpt là​​ $S=\left(1;+\mathrm{\infty }\right)\backslash \left\{2\right\}$.​​ Chọn D.

Câu​​ 72.​​ Gọi​​ $S$​​ là tập nghiệm của bất phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_{\mathrm{0,3}}\left(4x^2\right)\ge \mathrm{l}\mathrm{o}{\mathrm{g}}_{\mathrm{0,3}}\left(12x-5\right).$​​ Kí hiệu​​ $m,M$​​ lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của tập​​ $S$. Mệnh đề nào sau đây là đúng?

 A.​​ $m+M=3.$​​  B.​​ $m+M=2$.​​  C.​​ $M-m=3.$​​  D.​​ $M-m=1.$​​ 

Lời giải.​​ Điều kiện:​​ $x\ge \frac{5}{12}.$

Bất phương trình​​ $\iff 4x^2\le 12x-5\iff 4x^2-12x+5\le 0$

$$\iff \frac{1}{2}\le x\le \frac{5}{2}\left(\mathrm{t}\mathrm{h}\mathrm{o}\mathrm{a}\right)$$

Suy ra tập nghiệm của bất phương trình là​​ $S=\left[\frac{1}{2};\frac{5}{2}\right]$.

Suy ra​​ $m=\frac{1}{2}$​​ và​​ $M=\frac{5}{2}$​​ nên​​ $m+M=3.$​​ Chọn​​ A.

Câu​​ 73.​​ Tìm tập nghiệm​​ $S$​​ của bất phương trình​​ $\mathrm{l}\mathrm{o}\mathrm{g}10^{\mathrm{l}\mathrm{o}\mathrm{g}\left(x^2+21\right)}<1+\mathrm{l}\mathrm{o}\mathrm{g}x.$

 A.​​ $S=\left(3;7\right).$  B.​​ $S=\left(-\mathrm{\infty };3\right)\cup \left(7;+\mathrm{\infty }\right).$

 C.​​ $S=\left(-\mathrm{\infty };3\right).$  D.​​ $S=\left(7;+\mathrm{\infty }\right).$

Lời giải.​​ Điều kiện:​​ $x>0.$

Bất phương trình​​ $\iff \mathrm{l}\mathrm{o}\mathrm{g}\left(x^2+21\right).\mathrm{l}\mathrm{o}\mathrm{g}10<\mathrm{l}\mathrm{o}\mathrm{g}10+\mathrm{l}\mathrm{o}\mathrm{g}x$

$$\iff \mathrm{l}\mathrm{o}\mathrm{g}\left(x^2+21\right)<\mathrm{l}\mathrm{o}\mathrm{g}\left(10x\right)$$

$\iff x^2+21<10x\iff 3<x<7\left(\mathrm{t}\mathrm{h}\mathrm{o}\mathrm{û}\mathrm{a}\mathrm{m}\mathrm{a}\mathrm{õ}\mathrm{n}\right)\stackrel{}{\to }S=\left(3;7\right).$​​ Chọn A.

Câu 74.​​ Có bao nhiêu số nguyên dương​​ $x$​​ thỏa mãn bất phương trình​​ $\mathrm{l}\mathrm{o}\mathrm{g}\left(x-40\right)+\mathrm{l}\mathrm{o}\mathrm{g}\left(60-x\right)<2$?

 A.​​ 20. B.​​ 18. C.​​ 21. D.​​ 19.

Lời giải.​​ Điều kiện:​​ $40<x<60$.

Bất phương trình​​ $\iff \mathrm{l}\mathrm{o}\mathrm{g}\left[\left(x-40\right)\left(60-x\right)\right]<2$

$$\iff \left(x-40\right)\left(60-x\right)<10^2\iff x^2-100x+2500>0$$

$$\iff {\left(x-50\right)}^2>0\iff x\ne 50$$

Kết hợp với điều kiện, ta được​​ $\left\{\begin{array}{l}40<x<60\\ x\ne 50\end{array}\right.\stackrel{x\in {\mathbb{Z}}^{+}}{\to }x\in \left\{41;...;59\right\}\backslash \left\{50\right\}$.​​ Chọn B.

Câu​​ 75.​​ Biết rằng tập nghiệm của bất phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(1+\mathrm{l}\mathrm{o}{\mathrm{g}}_{\frac{1}{9}}x-\mathrm{l}\mathrm{o}{\mathrm{g}}_{9}x\right)<1$​​ có dạng​​ $S=\left(\frac{1}{a};b\right)$​​ với​​ $a,b$​​ là những số nguyên. Mệnh đề nào sau đây là đúng?

 ​​ A.​​ $a=-b$.​​  B.​​ $a+b=1$.​​  C.​​ $a=b$.​​  D.​​ $a=2b$.​​ 

Lời giải.​​ Điều kiện:​​ $\left\{\begin{array}{l}x>0\\ 1+\mathrm{l}\mathrm{o}{\mathrm{g}}_{\frac{1}{9}}x-\mathrm{l}\mathrm{o}{\mathrm{g}}_{9}x>0\end{array}\right.$

$$\iff \left\{\begin{array}{l}x>0\\ 1-2\mathrm{l}\mathrm{o}{\mathrm{g}}_{9}x>0\end{array}\right.\iff$$

$$\left[\begin{array}{l}x>0\\ \mathrm{l}\mathrm{o}{\mathrm{g}}_{9}x<\frac{1}{2}\end{array}\right.\iff \left\{\begin{array}{l}x>0\\ x<3\end{array}\right.\iff 0<x<3$$

Bất phương trình​​ $\iff 1-2\mathrm{l}\mathrm{o}{\mathrm{g}}_{9}x<2\iff \mathrm{l}\mathrm{o}{\mathrm{g}}_{9}x>-\frac{1}{2}\iff x>\frac{1}{3}.$

Đối chiếu với điều kiện, ta được tập nghiệm của bất phương trình là​​ $S=\left(\frac{1}{3};3\right)$.

Suy ra​​ $a=3,b=3$.​​ Chọn​​ C.​​ 

Câu​​ 76.​​ Có bao nhiêu giá trị nguyên của​​ $x$​​ trong đoạn​​ $\left[-2018;2018\right]$​​ thỏa mãn bất phương trình​​ $\mathrm{l}\mathrm{o}\mathrm{g}{}_{\frac{\pi }{4}}{}^{\mathrm{ }}\mathrm{ }\left[\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(x+\sqrt{2x^2-x}\right)\right]<0?$

 A.​​ $4033.$ B.​​ $4031.$ C.​​ $4037.$ D.​​ $2018.$

Lời giải.​​ Điều kiện:​​ $\left\{\begin{array}{ll}x+\sqrt{2x^2-x}>0& \left(1\right)\\ \mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(x+\sqrt{2x^2-x}\right)>0& \left(2\right)\end{array}\right.$.

Bất phương trình​​ $\mathrm{l}\mathrm{o}\mathrm{g}{}_{\frac{\pi }{4}}{}^{\mathrm{ }}\mathrm{ }\left[\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(x+\sqrt{2x^2-x}\right)\right]<\mathrm{l}\mathrm{o}\mathrm{g}{}_{\frac{\pi }{4}}{}^{\mathrm{ }}\mathrm{ }1$​​ 

$\iff \mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(x+\sqrt{2x^2-x}\right)>1$(thỏa​​ $\left(2\right)$)

$$\iff \mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(x+\sqrt{2x^2-x}\right)>\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}2$$​​ 

$\iff x+\sqrt{2x^2-x}>2$(thỏa​​ $\left(1\right)$)

$$\iff \sqrt{2x^2-x}>2-x$$

$$\iff \left[\begin{array}{l}\left\{\begin{array}{l}2-x<0\\ 2x^2-x\ge 0\end{array}\right.\\ \left\{\begin{array}{l}2-x\ge 0\\ 2x^2-x>{\left(2-x\right)}^2\end{array}\right.\end{array}\right.\iff \left[\begin{array}{l}x>1\\ x<-4\end{array}\right.$$

$$\stackrel{x\in \left[-2018;2018\right]}{\to }$$

$$x\in \left\{-2018;-2017;...;-6;-5;2;3;...;2017;2018\right\}$$

$\Rightarrow$​​ có​​ $4031$​​ giá trị nguyên của​​ $x$​​ thỏa mãn.​​ Chọn B.

Câu​​ 77.​​ Tìm tập nghiệm​​ $S$​​ của bất phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x+\mathrm{l}\mathrm{o}{\mathrm{g}}_{3}x>1+\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x\mathrm{l}\mathrm{o}{\mathrm{g}}_{3}x.$

 A.​​ $S=\left(3;+\mathrm{\infty }\right).$  B.​​ $S=\left(0;2\right)\cup \left(3;+\mathrm{\infty }\right).$ 

 C.​​ $S=\left(2;3\right).$  D.​​ $S=\left(-\mathrm{\infty };2\right)\cup \left(3;+\mathrm{\infty }\right).$

Lời giải.​​ Điều kiện:​​ $x>0$.

Bất phương trình​​ $\iff \left(\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x-\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x\mathrm{l}\mathrm{o}{\mathrm{g}}_{3}x\right)+\mathrm{l}\mathrm{o}{\mathrm{g}}_{3}x-1>0$

$$\iff \mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x\left(1-\mathrm{l}\mathrm{o}{\mathrm{g}}_{3}x\right)+\mathrm{l}\mathrm{o}{\mathrm{g}}_{3}x-1>0$$

$$\iff \left(1-\mathrm{l}\mathrm{o}{\mathrm{g}}_{3}x\right)\left(\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x-1\right)>0$$ $$\left(\mathrm{*}\right)$$​​ 

​​ TH1:​​ $\left\{\begin{array}{l}\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x-1>0\\ 1-\mathrm{l}\mathrm{o}{\mathrm{g}}_{3}x>0\end{array}\right.\iff \left\{\begin{array}{l}\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x>1\\ \mathrm{l}\mathrm{o}{\mathrm{g}}_{3}x<1\end{array}\right.$

$$\iff \left\{\begin{array}{l}x>2\\ x<3\end{array}\right.\iff 2<x<3\left(\mathrm{t}\mathrm{h}\mathrm{o}\mathrm{a}\right)$$

​​ TH2:​​ $\left\{\begin{array}{l}\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x-1<0\\ 1-\mathrm{l}\mathrm{o}{\mathrm{g}}_{3}x<0\end{array}\right.$

$\iff \left\{\begin{array}{l}\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x<1\\ \mathrm{l}\mathrm{o}{\mathrm{g}}_{3}x>1\end{array}\right.\iff \left\{\begin{array}{l}x<2\\ x>3\end{array}\right.$: vô nghiệm.

Vậy​​ tập nghiệm của bất phương trình​​ là​​ $S=\left(2;3\right)$.Chọn C.

Câu​​ 78.​​ Có tất cả bao nhiêu số nguyên thỏa mãn bất phương trình​​ $\mathrm{l}\mathrm{o}\mathrm{g}{}_{\frac{1}{2}}{}^{\mathrm{ }}\mathrm{ }\left[\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(2-x^2\right)\right]>0$?

 ​​ A.​​ $1$.​​  B.​​ $2$.​​  C.​​ $3$.​​  D.​​ $0$.​​ 

Lời giải.​​ Điều kiện:​​ $\left\{\begin{array}{l}2-x^2>0\\ \mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(2-x^2\right)>0\end{array}\right.$

$$\iff \left\{\begin{array}{l}2-x^2>0\\ 2-x^2>1\end{array}\right.\iff 2-x^2>1\iff -1<x<1$$

Bất phương trình​​ $\iff \mathrm{l}\mathrm{o}\mathrm{g}{}_{\frac{1}{2}}{}^{\mathrm{ }}\mathrm{ }\left[\mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(2-x^2\right)\right]>\mathrm{l}\mathrm{o}\mathrm{g}{}_{\frac{1}{2}}{}^{\mathrm{ }}\mathrm{ }1$

$$\iff \mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(2-x^2\right)<1\iff \mathrm{l}\mathrm{o}{\mathrm{g}}_2\left(2-x^2\right)<\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}2$$

$$\iff 2-x^2<2\iff x^2>0\iff x\ne 0.$$

Đối chiếu điều kiện, bất phương trình có tập nghiệm​​ $S=\left(-1;0\right)\cup \left(0;1\right)$.

Suy ra không có số nguyên nào thuộc tập​​ $S$.​​ Chọn D.

Câu 79.​​ Tìm tập nghiệm​​ $S$​​ của bất phương trình​​ $\mathrm{l}\mathrm{o}{\mathrm{g}}_{\frac{1}{2}}\left(\mathrm{l}\mathrm{o}{\mathrm{g}}_3\frac{2x+1}{x-1}\right)>0.$

 ​​ ​​ ​​ ​​​​  A.​​ $S=\left(-\mathrm{\infty };1\right)\cup \left(4;+\mathrm{\infty }\right).$ B.​​ $S=\left(-\mathrm{\infty };-2\right)\cup \left(1;+\mathrm{\infty }\right).$​​   ​​​​  

 C.​​ $S=\left(-2;1\right)\cup \left(1;4\right).$​​  D.​​ $S=\left(-\mathrm{\infty };-2\right)\cup \left(4;+\mathrm{\infty }\right).$

Lời giải.​​ Điều kiện:​​ $\left\{\begin{array}{l}\frac{2x+1}{x-1}>0\\ \mathrm{l}\mathrm{o}{\mathrm{g}}_3\frac{2x+1}{x-1}>0\end{array}\right.\iff \left\{\begin{array}{l}\frac{2x+1}{x-1}>0\\ \frac{2x+1}{x-1}>1\end{array}\right.$

$$\iff \frac{2x+1}{x-1}>1\iff \left[\begin{array}{l}x>1\\ x<-2\end{array}\right.$$

Bất phương trình​​ $\iff \mathrm{l}\mathrm{o}{\mathrm{g}}_3\frac{2x+1}{x-1}<1\iff \frac{2x+1}{x-1}<3$

$$\iff \frac{4-x}{x-1}<0\iff \left[\begin{array}{l}x<1\\ x>4\end{array}\right.$$

Đối chiếu điều kiện, ta được tập nghiệm​​ $S=\left(-\propto ;-2\right)\cup \left(4;+\propto \right).$​​ Chọn D.​​ 

Câu​​ 80.​​ Tìm tập nghiệm​​ $S$​​ của bất phương trình​​ $\frac{1-\mathrm{l}\mathrm{o}{\mathrm{g}}_{4}x}{1-\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x}\le \frac{1}{2}.$

 A.​​ $S=\left(0;2\right).$​​  B.​​ $S=\left[2;+\mathrm{\infty }\right).$ C.​​ $S=\left(-\mathrm{\infty };2\right).$ D.​​ $S=\left(2;+\mathrm{\infty }\right).$

Lời giải.​​ Điều kiện:​​ $\left\{\begin{array}{l}x>0\\ \mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x\ne 1\end{array}\right.\iff \left\{\begin{array}{l}x>0\\ x\ne 2\end{array}\right..$

Bất phương trình​​ $\iff \frac{1-\frac{1}{2}\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x}{1-\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x}\le \frac{1}{2}\iff$

$$\frac{2-\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x}{2\left(1-\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x\right)}\le \frac{1}{2}\iff \frac{2-\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x}{1-\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x}\le 1$$

$$\iff \frac{2-\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x}{1-\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x}-1\le 0\iff \frac{1}{1-\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x}\le 0\iff$$

$$1-\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x<0\iff \mathrm{l}\mathrm{o}{\mathrm{g}}_{2}x>1\iff x>2\left(\mathrm{t}\mathrm{h}\mathrm{o}\mathrm{a}\right).$$

Vậy tập nghiệm của bất phương trình là​​ $S=\left(2;+\mathrm{\infty }\right)$.​​ Chọn D.