Tích phân (Lý thuyết + 50 bài tập có lời giải)
Nội dung bài viết
1. Định nghĩa
Cho f là hàm số liên tục trên đoạn [a; b] Giả sử F là một nguyên hàm của f trên [a; b] Hiệu số F(b) - F(a) được gọi là tích phân từ a đến b (hay tích phân xác định trên đoạn [a; b] của hàm số f(x) kí hiệu là 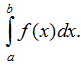
Ta dùng kí hiệu ![]() để chỉ hiệu số F(b) - F(a). Vậy
để chỉ hiệu số F(b) - F(a). Vậy 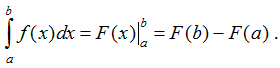 .
.
Nhận xét: Tích phân của hàm số f từ a đến b có thể kí hiệu bởi 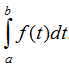 hay
hay 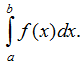 . Tích phân đó chỉ phụ thuộc vào f và các cận a, b mà không phụ thuộc vào cách ghi biến số.
. Tích phân đó chỉ phụ thuộc vào f và các cận a, b mà không phụ thuộc vào cách ghi biến số.
Ý nghĩa hình học của tích phân: Nếu hàm số f liên tục và không âm trên đoạn [a; b] thì tích phân 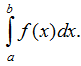 là diện tích S của hình thang cong giới hạn bởi đồ thị hàm số y = f(x) , trục Ox và hai đường thẳng x = a, x = b. Vậy S =
là diện tích S của hình thang cong giới hạn bởi đồ thị hàm số y = f(x) , trục Ox và hai đường thẳng x = a, x = b. Vậy S = 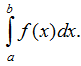
2. Tính chất của tích phân
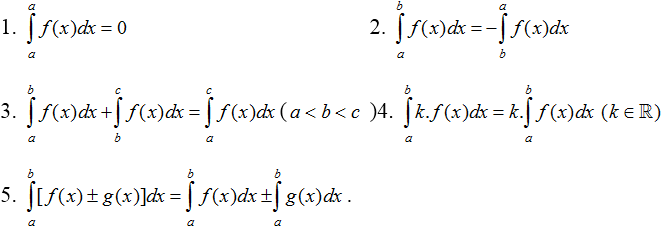
B. Bài tập
Câu 1: Tích phân
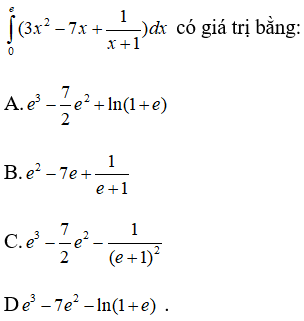
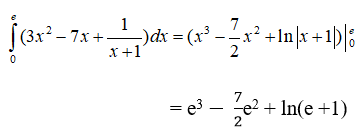
Ta chọn đáp án A
Câu 2: Cho hai tích phân:
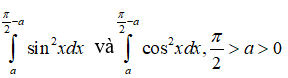
Trong các khẳng định sau , khẳng định nào đúng?
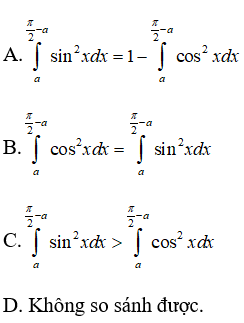
Đặt t = π/2 - x ⇒ dt = -dx Khi x = a thì t = π/2 - a , khi x = π/2 - a thì t = a
Ta có:
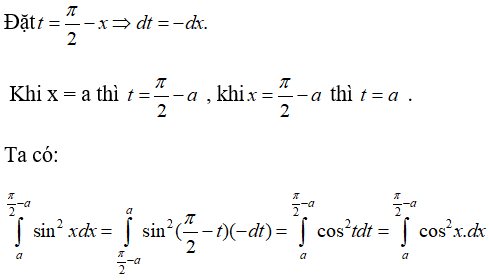
Vậy chọn đáp án B.
Câu 3:
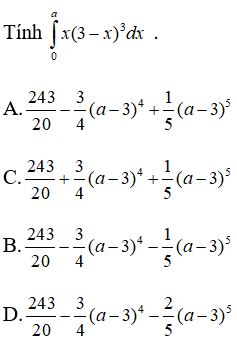
Đặt: t = 3 - x ⇒ dt = - dx .
Khi x = 0 thì t = 3, khi x = a thì t = 3-a.
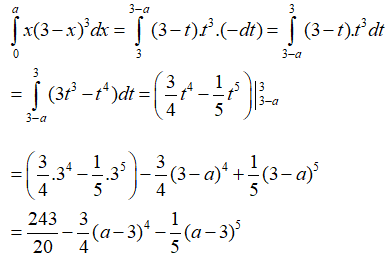
Vậy chọn đáp án B.
Câu 4: Tính tích phân
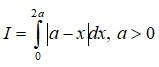
A. I = 0 B. I = a2 C. I = -a2 D. I = 2a2 .
Ta có:
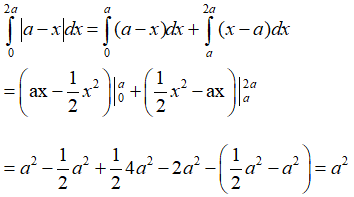
Vậy chọn đáp án B.
Câu 5: Tính tích phân 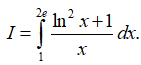
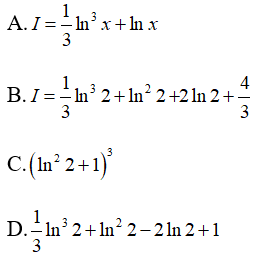
Đặt t = lnx ⇒ dt = (1/x)dx . Khi x = 1 thì t = 0, khi x = 2e thì t = 1+ln2. Ta có:
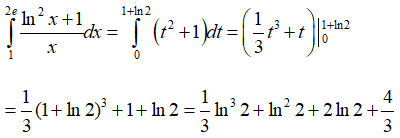
Vậy chọn đáp án D.
Câu 6: Tính tích phân
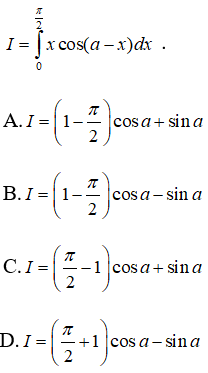
Đặt u = x và dv = cos(a - x)dx ,suy ra du = dx và v = -sin(a-x). Do đó
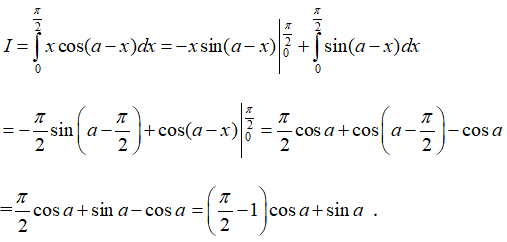
Vậy chọn đáp án C.
Câu 7:
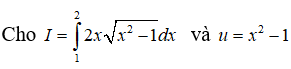
Khẳng định nào dưới đây là sai?

Đặt u = x2 - 1 , ta có du = 2xdx. Khi x = 1 thì u = 0, x = 2 thì u = 3. Do đó

Vậy chọn đáp án C.
Câu 8:
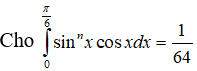
Tìm n?
A.6 B.5 C.4 D.3
Ta có:
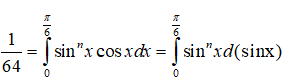
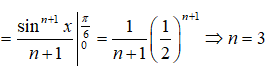
Vậy chọn đáp án D.
Câu 9: Kết quả của tích phân
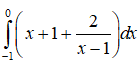
được viết dưới dạng a+bln2. Tính giá trị của a+b.
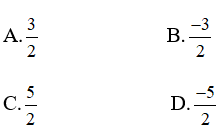
Ta có:
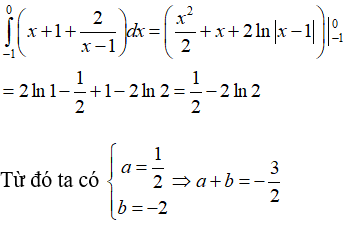
Vậy chọn đáp án D
Câu 10: Giả sử
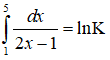
Giá trị của K là:
A.9 B.3 C.81 D.8
Ta có:
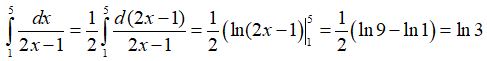
Do đó, K = 3
Câu 11: Cho:
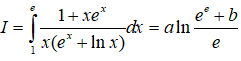
Tính giá trị của a-b.
A.3 B.1 C.2 D.0.
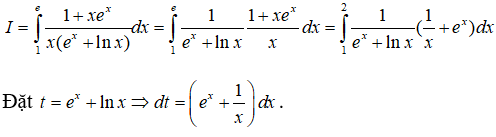
Khi x = 1 thì t = e, khi x = e thì t = ee + 1 .
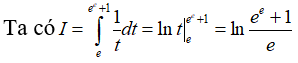
Từ đó suy ra: a = 1; b = 1 nên a – b = 0.
Câu 12: Cho
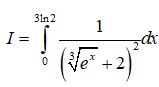
Giả sử đặt t = ∛ex + 2 thì ta được:

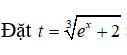 ⇒(t - 2)3 = ex
⇒(t - 2)3 = ex
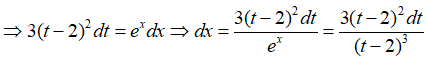
Đổi cận: x = 0 thì t = 3 ; x = 3ln2 thì t = 4
Khi đó
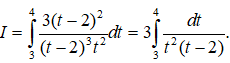
Câu 13: Cho
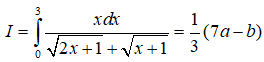
Khi đó a+b bằng
A.10+ √7 B.22 C. √7 + 6 D.Đáp án khác.
Ta có
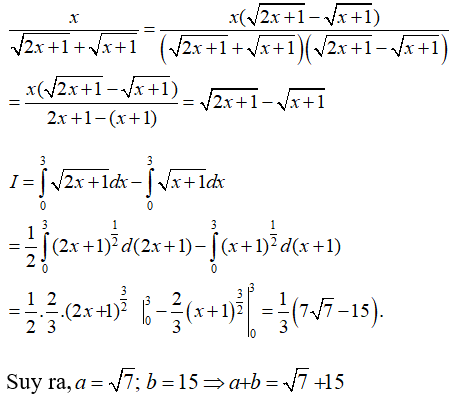
Câu 14: Cho
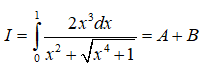
Đặt t = x2 . Biết
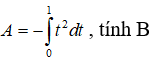
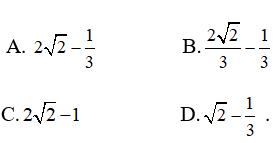
Đặt t = x2 ⇒ dt = 2xdx. Ta có:
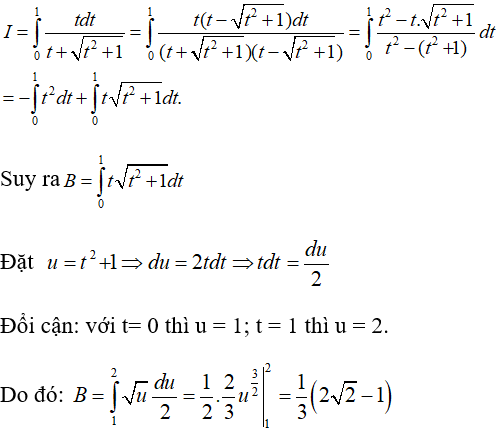
Câu 15: Nếu
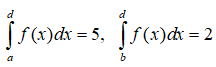
với a < d < b thì
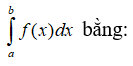
A.-2 B.3 C.8 D.0
Ta có:
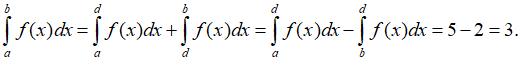
Câu 16: Cho tích phân
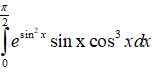
Nếu biến đổi số t = sin2x thì:
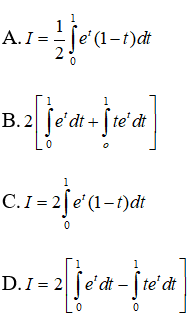
Ta có
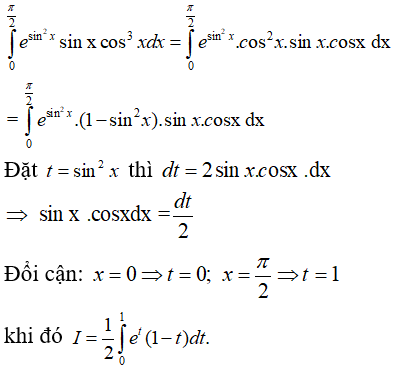
Câu 17: Biết
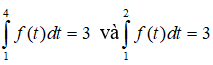
Phát biểu nào sau đây nhận giá trị đúng?

Ta có
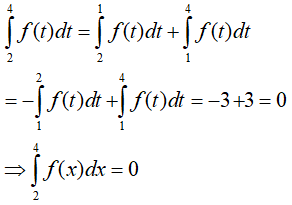
Câu 18:
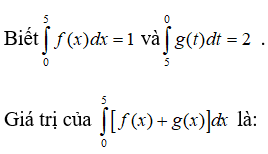
A. Không xác định được B.1
C.3 D.-1
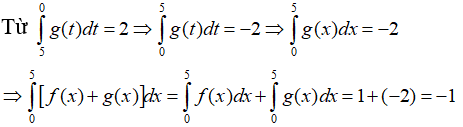
Bài 19: Tích phân ![]() bằng
bằng
A. L = π B. L = -π C. L = -2 D. L = 0
Đáp án : A
Giải thích :
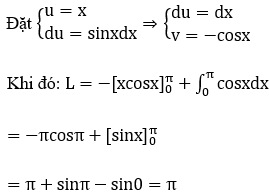
Bài 20: Tích phân ![]() bằng
bằng

Đáp án : D
Giải thích :
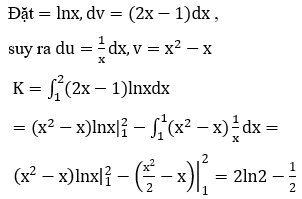
Bài 21: Tích phân ![]() bằng
bằng
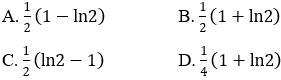
Đáp án : A
Giải thích :
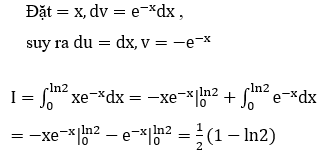
Bài 22: Tích phân ![]() bằng
bằng

Đáp án : A
Giải thích :
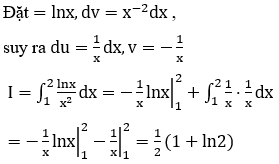
Bài 23: Tích phân ![]() có giá trị là
có giá trị là
A. e+2 B. 2-e C. e-2 D. e
Đáp án : C
Giải thích :
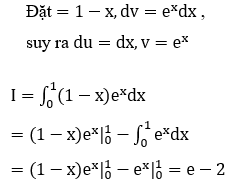
Bài 24: Tích phân ![]() là
là
A. 3ln3 B. 2ln2 C. 3ln3-2 D. 2-3ln3
Đáp án : C
Giải thích :
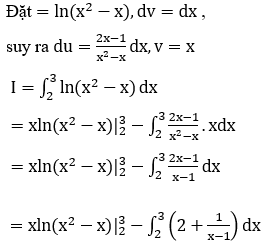
![]()
Bài 25: Tìm a > 0 sao cho ![]()
A. 4 B. 1/4 C. 1/2 D. 2
Đáp án : D
Giải thích :
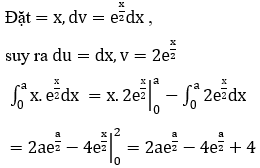
Bài 26: Giá trị của tích phân ![]()

Đáp án : B
Giải thích :
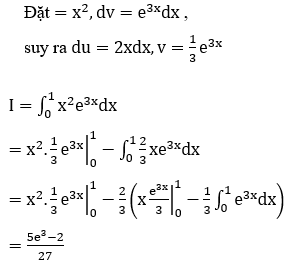
Bài 27: Tích phân ![]() bằng
bằng
A. π2-4 B. π2+4 C. 2π2-3 D. 2π2+3
Đáp án : A
Giải thích :
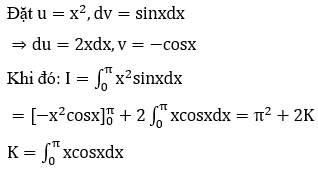

Bài 28: Tính tích phân 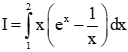
A. I=e2-1 B. I=e2 C. I=e2+1 D. I=e2-2
Đáp án : A
Giải thích :
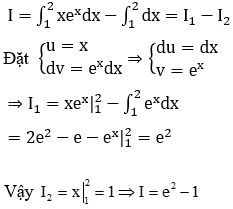
Bài 29: Tính tích phân
![]()

Đáp án :
Giải thích :
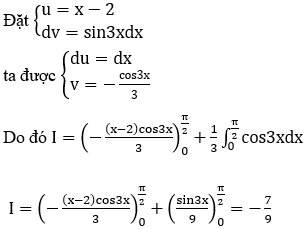
Bài 30: Tính tích phân
![]()

Đáp án :
Giải thích :
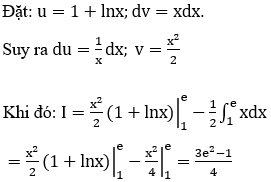
Bài 31: Tính tích phân sau
![]()
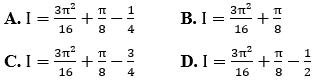
Đáp án :
Giải thích :

Bài 32: Tính tích phân
![]()
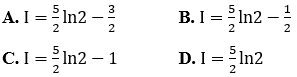
Đáp án :
Giải thích :
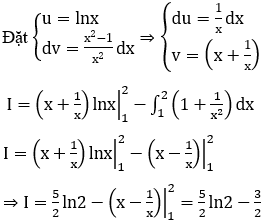
Bài 33: Tính tích phân
![]()
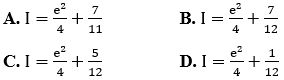
Đáp án :
Giải thích :

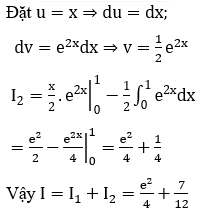
Bài 34: Tính tích phân
![]()

Đáp án :
Giải thích :
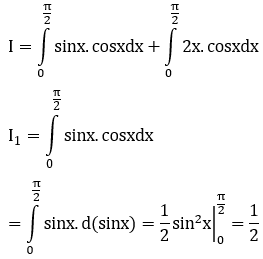
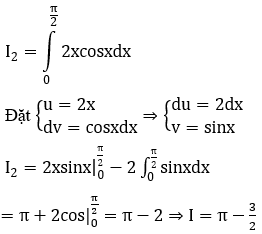
Bài 35: Tính tích phân
![]()

Đáp án :
Giải thích :
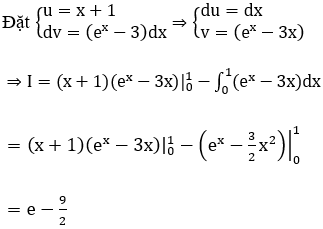
Bài 36: Tính tích phân
![]()

Đáp án :
Giải thích :
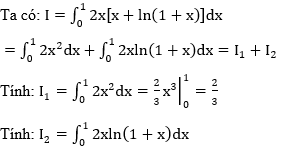
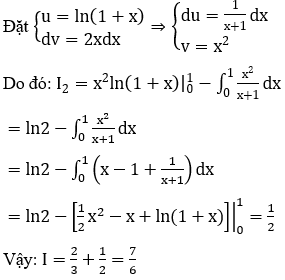
Bài 37: Tính tích phân
![]()

Đáp án :
Giải thích :
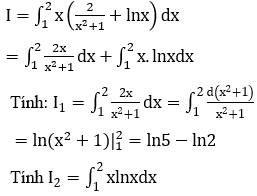
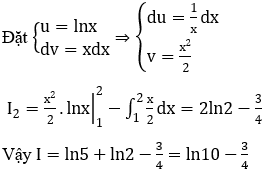
Bài 38: Tính tích phân
![]()
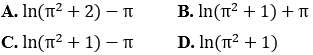
Đáp án :
Giải thích :
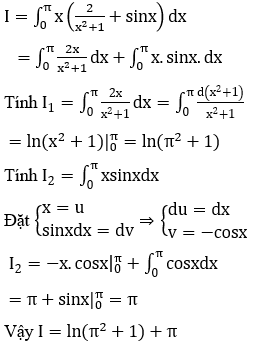
Bài 39: Tính các tính phân sau:
a)I = ![]() .
.
A. 1 B. 1/6 C. 2/9 D. 3/8
b)I = ![]() .
.
A. 1 - ln5 B. 1 + ln3 C. 2 - ln4 D. 1 - ln2
a)
![]()
Đáp án: D
b)
![]()
Đáp án: D
Bài 40: Tính tích phân I = ![]() |x - 1|dx ta được kết quả :
|x - 1|dx ta được kết quả :
A.1 B.2 C.3 D.4
Cho x - 1 = 0 ⇔ x = 1 ( thỏa mãn)
Ta có bảng xét dấu :
![]()
Khi đó :
I = -![]() (x - 1)dx +
(x - 1)dx + ![]() (x - 1)dx =
(x - 1)dx = 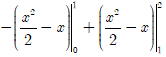 = 1
= 1
Đáp án: A
Bài 41: Tính tích phân I = ![]() |x2 - 1|dx ta được kết quả :
|x2 - 1|dx ta được kết quả :
A. 4 B. 3 C. 9 D. 9/2
Cho x2 - 1 = 0 ⇔ x = 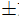
Bảng xét dấu của x2 - 1 trên đoạn [-2;2]
![]()
I = ![]() |x2 - 1|dx =
|x2 - 1|dx = ![]() (x2 - 1)dx +
(x2 - 1)dx + ![]() (1 - x2)dx +
(1 - x2)dx + ![]() (x2 - 1)dx
(x2 - 1)dx
=  = 4
= 4
Đáp án: A
Bài 42: Tính các tích phân sau.
a) I = ![]()
A. 3 + 6ln3 B. 3ln2 - ln3 C. 6 - 2ln3 D. 3 + 6ln2 - 3ln3
b) I = ![]()
A. 0 B. 1 C. ln3 + ln4 D. ln3 - ln4
a)Ta có
I = ![]() =
= 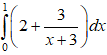 = (2x + 3.ln(x + 3))
= (2x + 3.ln(x + 3))
Đáp án: D
b)Ta có
I = ![]() =
= 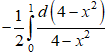 = ln|4 - x2|
= ln|4 - x2|![]() = ln3 - ln4
= ln3 - ln4
Đáp án: D
Bài 43: Tính các tích phân sau
a/ ![]() (x3 - 1)dx
(x3 - 1)dx
A.1 B: -1/2 C. -3/4 D. Tất cả sai
b/ ![]()
A.5 B.5,5 C. 6 D.6,5
a)![]() (x3 - 1)dx =
(x3 - 1)dx = ![]() x3dx -
x3dx - ![]() xdx = (
xdx = (![]() - x)
- x)![]() = -3/4
= -3/4
Đáp án: C
b)![]() =
= ![]() (x + 4)dx = (
(x + 4)dx = (![]() + 4x)
+ 4x)![]() = (2 + 8) - (
= (2 + 8) - (![]() + 4) = 5,5
+ 4) = 5,5
Đáp án: B
Bài 44: Tính tích phân sau A = ![]()
A. -1/3 B. 2 C. 1/3 D: đáp án khác
Đặt t = 1 + x2 ⇒ dt = 2xdx ; Đổi cận: Khi x = 0 ⇒ t = 1; Khi x = 1 ⇒ t = 2
⇒ A = ![]()
![]() √t.dt =
√t.dt = ![]() =
= ![]() (2√2 - 1 )
(2√2 - 1 )
Đáp án: D
Bài 45: Tính tích phân sau B = ![]() x3(x4 - 1)5dx
x3(x4 - 1)5dx
A. -1/12 B. -1/6 C. -1/24 D.-1
Đặt t = x4 - 1 ⇒ dt = 4x3dx ;
Đổi cận: Khi x = 0 ⇒ t = -1; x = 1 ⇒ t = 0
⇒ B = ![]()
Đáp án: C
Bài 46: Tính tích phân sau C = ![]()
A.1 B. 2 C. ln(e-1) D. ln(e+1)
Đặt t = ex - 1 ⇒ dt = exdx
Đổi cận: Khi x = 1 ⇒ t = e – 1;Khi x = 2 ⇒ t = e2 - 1
⇒ C = 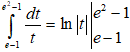 = ln(e2 - 1) - ln(e - 1) =
= ln(e2 - 1) - ln(e - 1) = ![]() = ln(e + 1)
= ln(e + 1)
Đáp án: D
Bài 47: Tính tích phân sau D = ![]()
A. 1 B. 2 C. 3 D. Tất cả sai
Đặt t = 4 - x2 ⇒ dt = -2xdx ⇒ xdx = -![]() dt
dt
Khi x = 0 ⇒ t = 4 ; x = 2 ⇒ t = 0
⇒ D = 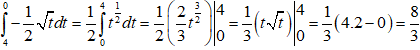
Đáp án: D
Bài 48: Tính tích phân I = ![]() |x2 - 3x + 2|dx ta được kết quả :
|x2 - 3x + 2|dx ta được kết quả :
A. 4 B. 3 C. 2 D. 1
Cho x2 - 3x + 2 = 0 ⇔ ![]() ( thỏa mãn)
( thỏa mãn)
Bảng xét dấu của x2 - 3x + 2 trên đoạn [0;2]
![]()
Khi đó :
I = ![]() (x2 - 3x + 2)dx -
(x2 - 3x + 2)dx - ![]() (x2 - 3x + 2)dx
(x2 - 3x + 2)dx
= 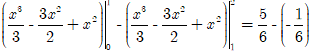 = 1
= 1
Đáp án: D
Bài 49: Tính tích phân sau E = 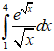
A. 2(e2 -e) B. e C. e2+e D. 2e2-1
Đặt t = √x ⇒ dt = ![]() dx ⇒
dx ⇒ ![]() = 2dt
= 2dt
Khi x = 1 ⇒ t = 1 ; x = 4 ⇒ t = 2 ; ⇒ E = ![]() 2.etdt = 2.et
2.etdt = 2.et![]() = 2(e2 -e)
= 2(e2 -e)
Đáp án: A
Bài 50: Tính tích phân sau F = 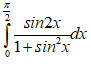
A. 1 B. ln2 C. ln3 D. 2
Đặt t = sin2x ⇒ dt = 2.sinx.cosxdx = sin2xdx
Khi x = 0 ⇒ sin20 = 0 ⇒ t = 0; x = ![]() ⇒
⇒ ![]() = 1 ⇒ t = 1
= 1 ⇒ t = 1
⇒ F = ![]() = ln|1 + t|
= ln|1 + t|![]() = ln2 - ln1 = ln2
= ln2 - ln1 = ln2
Đáp án: B
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.