1. Diện tích hình phẳng
a) Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x) liên tục trên đoạn [a; b], trục hoành và hai đường thẳng x = a, x = b được xác định: 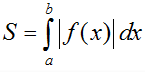
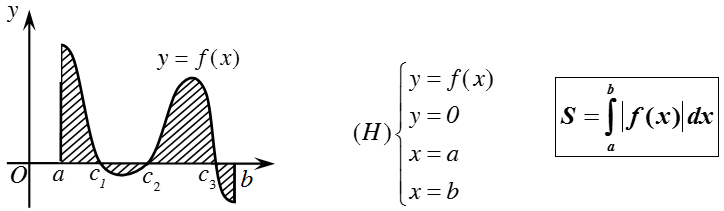
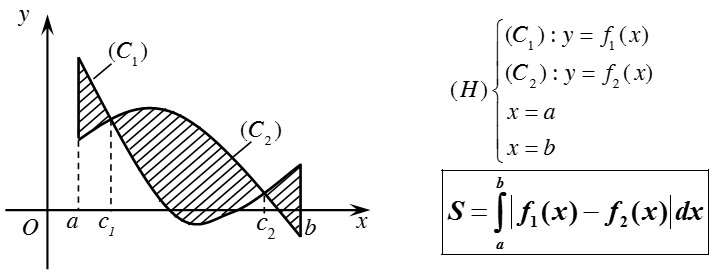
b) Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), y = g(x) liên tục trên đoạn [a; b] và hai đường thẳng x = a, x = b được xác định: : 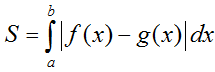
Chú ý:
- Nếu trên đoạn [a; b], hàm số f(x) không đổi dấu thì: 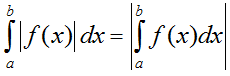
- Nắm vững cách tính tích phân của hàm số có chứa giá trị tuyệt đối
- Diện tích của hình phẳng giới hạn bởi các đường x = g(y), x = h(y) và hai đường thẳng y = c, y = d được xác định: 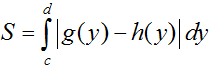
2. Thể tích vật thể và thể tích khối tròn xoay
a) Thể tích vật thể:
Gọi B là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm a và b; S(x) là diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm x, (a ≤ x ≤ b). Giả sử S(x) là hàm số liên tục trên đoạn [a; b].
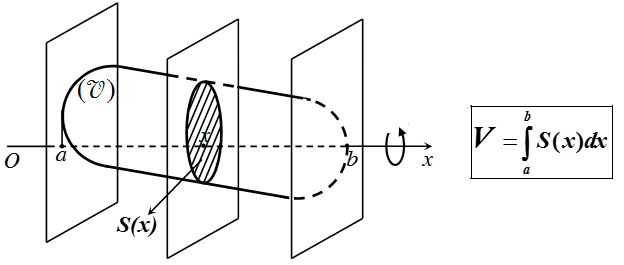
Khi đó, thể tích của vật thể B được xác định: 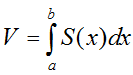
b) Thể tích khối tròn xoay:
Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường y = f(x) , trục hoành và hai đường thẳng x = a, x = b quanh trục Ox:
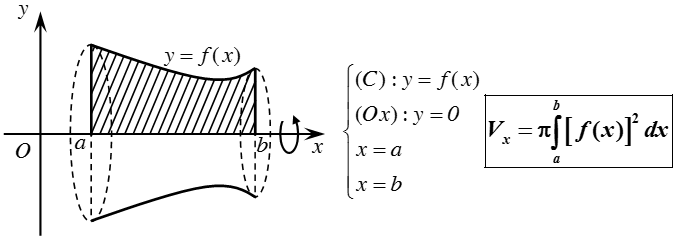
Chú ý:
- Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường x = g(y), trục hoành và hai đường thẳng y = c, y = d quanh trục Oy:
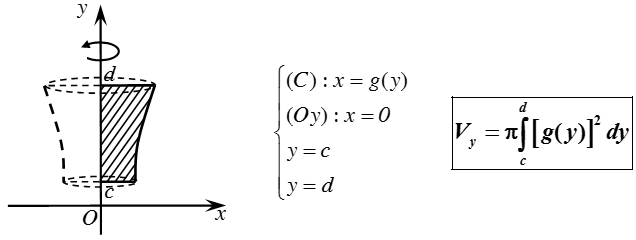
- Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường y = f(x), y = g(x) và hai đường thẳng x = a, x = b quanh trục Ox:
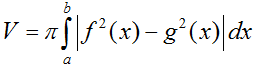
B. Bài tập trắc nghiệm
Câu 1: Viết công thức tính thể tích V của khối tròn xoay được tạo ra khi quay hình thang cong giới hạn bởi đồ thị hàm số y = f(x), trục Ox và hai đường thẳng x = a, x = b (a < b) quanh trục Ox.
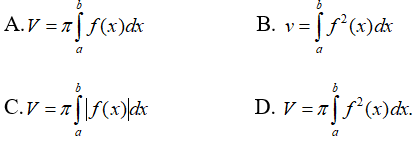
Chọn đáp án D
Câu 2: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số x3 - x và đồ thị hàm số y = x - x2.
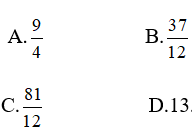
Tìm hoành độ các giao điểm của hai đồ thị, ta có:
x3 - x = x - x3 <=> x3 + x2 - 2x = 0
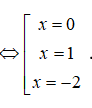
Vậy diện tích của hình phẳng tính là
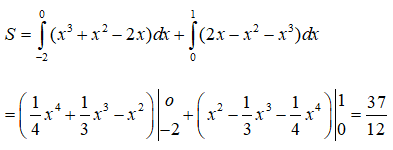
Vậy chọn đáp án B.
Câu 3: Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số y = (x -1)e2x ,trục tung và đường thẳng y = 0. Tính thể tích của khối tròn xoay thu được khi quay hình (H) quanh trục Ox
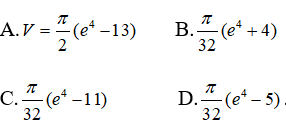
Tìm hoành độ giao điểm của hai dồ thị, ta có:
(x - 1)e2x = 0 => x = 1
Vậy thể tích của khối tròn xoay thu được khi quay (H) quanh Ox được tính bởi
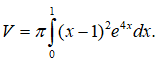
Đặt: u = (x - 1)2, dv e4xdx. Ta có du = 2(x -1)dx và v = e4x/4 .
Áp dụng công thức tích phân từng phần ta được
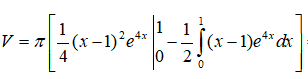
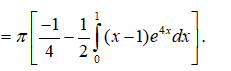
Đặt u1 = x - 1, dv1 = e4xdx , ta có du1 = dx, v1 = e4x/4 .
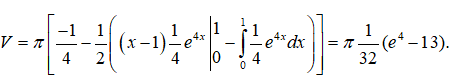
Vậy chọn đáp án A.
Câu 4: Sau chiến tranh thế giới thứ hai, tốc độ sinh ở cả nước phương Tây tăng rất nhanh. Giả sử rằng tốc độ sinh được cho bởi: b(t) = 5 + 2t, 0 ≤ t ≤ 10 , ( ở đó t số năm tính từ khi chiến tranh kết thúc, b(t) tính theo đơn vị triệu người).
a) Có bao nhiêu trẻ được sinh trong khoảng thời gian này ( tức là trong 10 năm đầu tiên sau chiến tranh)?
A. 100 triệu B. 120 triệu C. 150 triệu D. 250 triệu.
b) Tìm khoảng thời gian T sao cho số lượng trẻ được sinh ra là 14 triệu kể từ khi kết thức chiến tranh.
A. 1 năm B. 2 năm C. 3 năm D. 4 năm.
a) Để tìm số trẻ mới sinh, chúng ta sẽ tính tích phân tỉ lệ sinh b(t) trên khoảng thời gian 10 năm đầu tiên sau chiến tranh
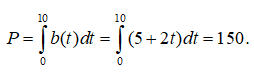
Vậy số trẻ được sinh cần tìm là 150 triệu.
Chọn đáp án C.
b) Số lượng trẻ mới sinh trong khoảng thời T bằng:
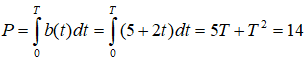
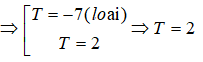
Vậy chọn đáp án B.
Câu 5: Diện tích hình phẳng giới hạn bởi y = x2 - x + 3 và y = 2x + 1 là:
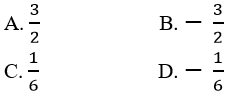
Ta có: x2 - x + 3 = 2x + 1 <=> x2 - 3x + 2 = 0 <=> x = 2 hoặc x = 1
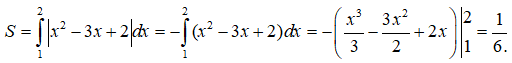
Câu 6: Cho đồ thị hàm số y = f(x). Diện tích hình phẳng ( phần gạch sọc ) là:
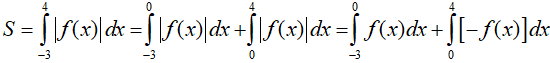
Câu 7: Diện tích hình phẳng giới hạn bởi đồ thị hai hàm số y = √6 và y = 6 - x và trục tùng là:
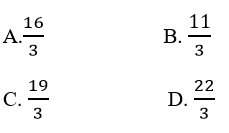
Diện tích giới hạn được tính bởi
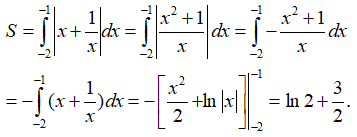
Câu 8: Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x + 1/x , trục hoành, đường thẳng x = -1 và đường thẳng x = -2 là:
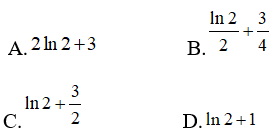

Câu 9: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = ex - e-x , trục hoành, đường thẳng x = -1 và đường thẳng x = 1.
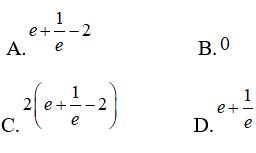
Diện tích hình phẳng được tính bởi
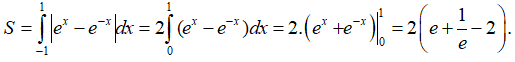
Câu 10: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = √x - x và trục hoành.
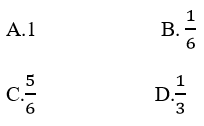
Xét phương trình
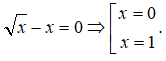
Khi đó diện tích hình phẳng được tính bởi
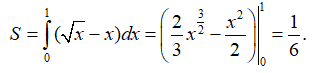
Câu 11: Gọi h(t) (cm) là mức nước ở bồn chứa sau khi bơm nước được t giây. Biết rằng
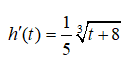
và lúc đầu bồn không có nước. Mức nước ở bồn sau khi bơm nước được 6 giây xấp xỉ bằng:
A. 2,65cm B. 2,66cm C. 2,67cm D. 2,68cm.
Mức nước trong bồn tại giây thứ t bằng:
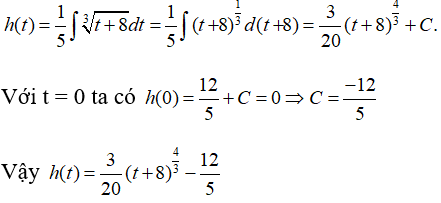
Khi đó h(6) ≈ 2,66 cm .
Câu 12: Vận tốc của một vật chuyển động là
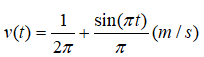
Quãng đường vật di chuyển trong khoảng thời gian 1,5 giây xấp xỉ bằng:
A. 0,33m B. 0,34m C. 0,35m D. 0,36m.
Câu 12: Vận tốc của một vật chuyển động là
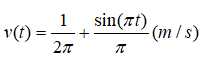
Quãng đường vật di chuyển trong khoảng thời gian 1,5 giây xấp xỉ bằng:
A. 0,33m B. 0,34m C. 0,35m D. 0,36m.
Quãng đường vật di chuyển sau thời gian 1,5 giây bằng
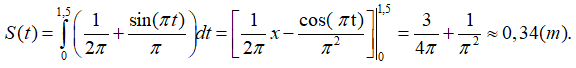
Câu 13: Thể tích phần vật thể giới hạn bởi hai mặt phẳng x = 0 và x = 3 biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x(0 ≤ x ≤ 3) là một hình chữ nhật có hai kích thước là x và 2√(9-x2)
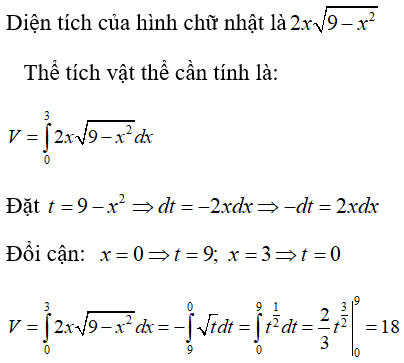
Câu 14: Thể tích khối xoay khi quay quanh trục hoành một hình phẳng giới hạn bởi đồ thị hàm số y = x(x-4) và trục hoành là:
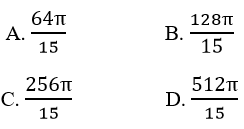
Phương trình hoành độ giao điểm của đồ thị và trục hoành :
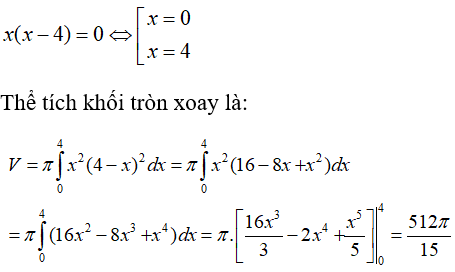
Câu 15: Thể tích khối tròn khi quay quanh trục hoành một hình phẳng giới hạn bởi đồ thị hàm số y = sinxcosx, y = 0, x = 0, x = π/2 là:
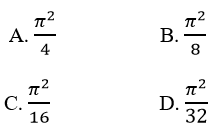
Thể tích khối tròn xoay là :
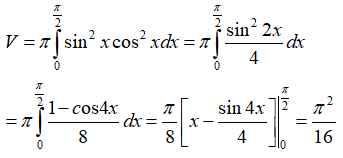
Câu 16: Thể tích khối tròn xoay khi quay quanh trục hoành một hình phẳng giới hạn bởi đồ thị hàm số y = lnx, y = 0, x = 2 là:
A. π(ln22 - 2ln2 + 1) B. 2π(ln22 - 2ln2 + 1)
C. 4π(ln22 - ln2 + 1) D. 2π(ln22 - ln2 + 1)
Phương trình giao điểm của đồ thị hàm số và trục hoành :
ln x = 0 ⇔ x = 1
Thể tích khối tròn xoay cần tính là :
âu 17: Thể tích khối tròn xoay khi quay quanh trục tung một hình phẳng giới hạn bởi hình tròn tâm I(2;0) bán kính R = 1 là:
A. π2 B. 2π2 C. 4π2 D. 8π2
Phương trình đường tròn tâm I(2 ; 0), bán kính R = 1 là :
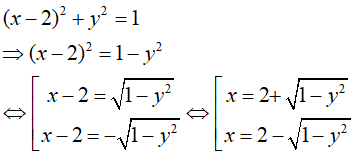
Đường tròn cắt trục tung tại hai điểm (0; 1) và( 0; -1).
Vậy ta có:
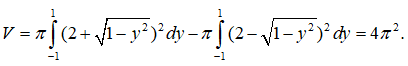
Câu 18. Tính diện tích các hình phẳng giới hạn bởi: Đồ thị các hàm số y=x2−4,y=−x2−2x và hai đường thẳng x=−3,x=−2;
A. 116
B. 113
C. 223
D. 193
Đáp án: B
Giải thích:
Dựa vào hình vẽ ta thấy diện tích hình phẳng cần tìm là:
S =∫−2−3|(x2−4)−(−x2−2x)|dx
=∫−2−3[(x2−4)−(−x2−2x)]dx
=∫−2−3(2x2+2x−4)dx
=(2x33+2x22−4x)|−2−3=113
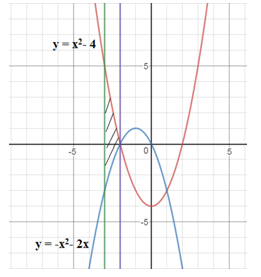
Câu 19: Đồ thị hai hàm số y=x2−4 và y=−x2−2x
A. 8
B. 10
C. 20
D. 9
Đáp án: D
Giải thích:
Phương trình hoành độ giao điểm đồ thị hai số đã cho là:
x2−4=−x2−2x
⇔x2+x−2=0
⇔[x=1x=−2
Dựa vào hình vẽ ở câu A. ta có:
S =∫1−2|(x2−4)−(−x−2x)|dx
=∫1−2[−(2x2+2x−4)]dx
=(−2x33−2x22+4x)|1−2=9
Câu 20: Đồ thị hàm số y=x3−4x , trục hoành, đường thẳng x=−2 và đưởng thẳng x=4.
A. 44
B. 24
C. 48
D. 28
Đáp án: A
Giải thích:
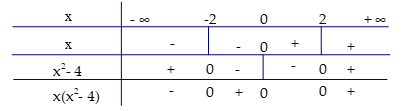
Diện tích cần tìm S=∫1−2|x3−4x|dx
Ta có: x3−4x=x(x2−4)=0
⇔[x=0x=±2
Ta có bảng xét dấu sau:
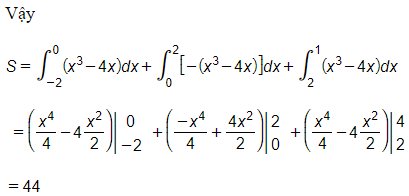
Câu 21: Hàm số y=x4−4x2+4,y=x2, trục tung và đường thẳng
A. 3825
B. 3835
C. 3815
D. 385
Đáp án: C
Giải thích:
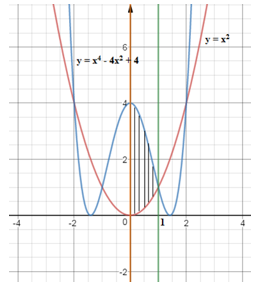
Diện tích hình phẳng cần tìm là:
S=∫10|x4−4x2+4−x2|dx
=∫10|x4−5x2+4|dx
Vì x4−5x2+4=(x2−1)(x2−4)≥0
∀x∈[0;1]
Nên
S=∫10(x4−5x2+4)dx
=(x55−5x33+4x)|10
=15−53+4=3815
Câu 22: Tính diện tích hình phẳng giới hạn bởi đồ thị hai hàm số y=x2+1 và y=3−x
A. 62
B. 52
C. 112
D. 92
Đáp án: D
Giải thích:
Hoành độ giao điểm đồ thị hai hàm số y=x2+1 và y=3−x là nghiệm của phương trình x2+1=3−x
⇔x2+x−2=0
⇔[x=1x=−2
Vậy diện tích cần tìm là:
S=∫1−2|(x2+1)−(3−x)|dx
=∫1−2|x2+x−2|dx
=−∫1−2(x2+x−2)dx
=−(x33+x22−2x)|1−2
=92
Câu 23: Tính diện tích hình phẳng giới hạn bởi các đường có phương trình x=y3,y=1 và x=8
A. 174
B. 172
C. 178
D. 274
Đáp án: A
Giải thích:
Tung độ giao điểm của đường cong x=y3 và đường thẳng x=8 là nghiệm của phương trình y3=8⇔y=2. Vậy diện tích cần tìm là:
S=∫21|y3−8|dy
=∫21(y3−8)dy
=−(y44−8y)|21
=−[(164−16)−(14−8)]
=174
Câu 24: Đồ thị hai hàm số y=√x,y=6−x và trục hoành.
A. 233
B. 223
C. 253
D. 293
Đáp án: B
Giải thích:
Ta có: y=√x⇔x=y2(y≥0);
y=6−x⇔x=6−y
Tung độ giao điểm của hai đường thẳng x=y2,x=6−y là nghiệm của phương trình y2=6−y ⇔y2+y−6=0 ⇔[y=−3 (L vi y≥0)y=2
Vậy diện tích cần tìm là S=∫20|y2−(6−y)|dy
=∫20|y2+y−6|dy
=−∫20(y2+y−6)dy
=−(y33+y22−6y)|20
=−(83+42−12)=223
Câu 25. Tính diện tích các hình phẳng giới hạn bởi: Đồ thị các hàm số y=4−x2, y=−x+2
A. 92
B. 225
C. 113
D. 253
Đáp án: A
Giải thích:
Ta có 4−x2=−x+2
⇔x2−x−2=0
⇔[x=−1x=2
Vậy diện tích hình phẳng cần tìm là:
S=∫2−1|(−x+2)−(4−x2)|dx
=∫2−1|x2−x−2|dx
=−∫2−1(x2−x−2)dx
=−(x33−x22−2x)|2−1
=−[(83−42−4)−(−13−12+2)]
=92
Câu 26. Cho hình phẳng (H) được giới hạn bởi đồ thị hàm số y=√ex và các đường thẳng y=0, x=0 và x=2. Thể tích V của khối tròn xoay được tạo thành khi quay hình phẳng (H) quanh trục Ox được tính bởi công thức nào sau đây?
A. V=π2∫0exdx.
B. V=π2∫0e2xdx.
C. V=π2∫0ex2dx.
D. V=2∫0ex2dx.
Đáp án: A
Giải thích:
Ta có: V=π2∫0(√ex)2dx
=π2∫0exdx.
Câu 27. Gọi (H) là hình phẳng giới hạn bởi đồ thị y=ex, trục Ox và hai đường thẳng x=0, x=1. Thể tích của khối tròn xoay khi quay (H) xung quanh trục Ox là
A. π2(e2−1).
B. π(e2+1).
C. π2(e2+1).
D. π(e2−1).
Đáp án: A
Giải thích:
V=π1∫0(ex)2dx
=π1∫0e2xdx
=π2e2x|10
=π2(e2−e0)
=π2(e2−1)
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.