I. NGUYÊN HÀM VÀ TÍNH CHẤT
1. Nguyên hàm
Định nghĩa: Cho hàm số f(x) xác định trên K (K là khoảng, đoạn hay nửa khoảng). Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F'(x) = f(x) với mọi x ∈ K.
Định lí:
1) Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì với mỗi hằng số C, hàm số G(x) = F(x) + C cũng là một nguyên hàm của f(x) trên K.
2) Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C, với C là một hằng số.
Do đó F(x) + C, C ∈ R là họ tất cả các nguyên hàm của f(x) trên K. Ký hiệu ∫f(x)dx = F(x) + C
2. Tính chất của nguyên hàm
Tính chất 1: (∫f(x)dx)' = f(x) và ∫f'(x)dx = f(x) + C
Tính chất 2: ∫kf(x)dx = k∫f(x)dx với k là hằng số khác 0.
Tính chất 3: ∫[f(x) ± g(x)]dx = ∫f(x)dx ± ∫g(x)dx
3. Sự tồn tại của nguyên hàm
Định lí: Mọi hàm số f(x) liên tục trên K đều có nguyên hàm trên K.
4. Bảng nguyên hàm của một số hàm số sơ cấp
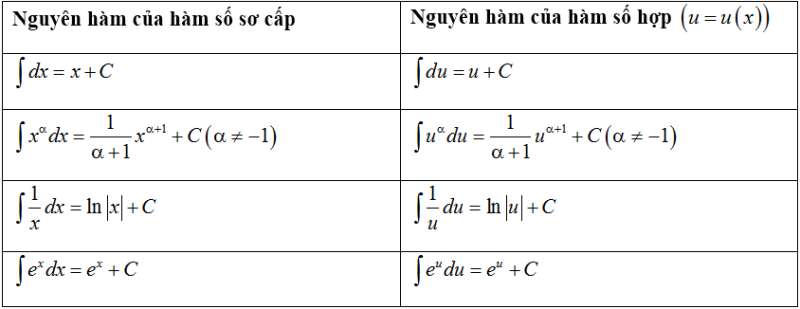
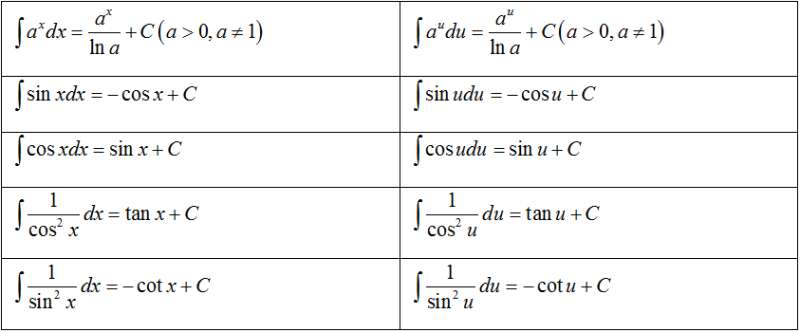
II. PHƯƠNG PHÁP TÍNH NGUYÊN HÀM
1. Phương pháp đổi biến số
Định lí 1: Nếu ∫f(u)du = F(u) + C và u = u(x) là hàm số có đạo hàm liên tục thì
∫f(u(x))u'(x)dx = F(u(x)) + C
Hệ quả: Nếu u = ax + b (a ≠ 0) thì ta có ∫f(ax + b)dx = (1/a)F(ax + b) + C
2. Phương pháp nguyên hàm từng phần
Định lí 2: Nếu hai hàm số u = u(x) và y = y(x) có đạo hàm liên tục trên K thì
∫u(x)v'(x)dx = u(x)v(x) - ∫u'(x)v(x)dx
Hay ∫udv = uv - ∫vdu
B. Bài tập trắc nghiệm
A.
B.
C.
D.
Hướng dẫn giải:
Sử dụng bảng nguyên hàm.
⟶ Chọn A
A. f(x) = 15x2 + 8x – 7
B. f(x) = 5x2 + 4x + 7
C.
D. f(x) = 5x2 + 4x – 7
Hướng dẫn giải:
Lấy đạo hàm của hàm số F(x) ta được kết quả.
⟶ Chọn A
A.
B.
C.
D.
Hướng dẫn giải:
Sử dụng bảng nguyên hàm.
⟶ Chọn A
A.
B.
C.
D.
Hướng dẫn giải:
f(x) = (x + 1)(x + 2) = x2 + 3x + 2. Sử dụng bảng nguyên hàm.
⟶ Chọn A
A.
B.
C.
D.
Hướng dẫn giải:
Sử dụng bảng nguyên hàm.
⟶ Chọn A
A.
B.
C. ∫sin2x dx = cos2x + C
D. ∫sin2x dx = –cos2x + C
Hướng dẫn giải:
⟶ Chọn A
A.
B.
C.
D.
Hướng dẫn giải:
⟶ Chọn A
A.
B.
C.
D.
Hướng dẫn giải:
nên
⟶ Chọn A
A.
B.
C.
D.
Hướng dẫn giải:
⟶ Chọn A
A.
B.
C.
D.
Hướng dẫn giải
⟶ Chọn A
A. ∫f(x) dx = ex + e–x + C
B. ∫f(x) dx = –ex + e–x + C
C. ∫f(x) dx = ex – e–x + C
D. ∫f(x) dx = –ex – e–x + C
Hướng dẫn giải:
∫(ex – e–x) dx = ex + e–x + C
⟶ Chọn A
A.
B.
C.
D.
Hướng dẫn giải:
⟶ Chọn A
A. F(x) = 3ex + x + C
B. F(x) = 3ex + ex lnex + C
C.
D. F(x) = 3ex – x + C
Hướng dẫn giải:
F(x) = ∫ex (3 + e–x) dx = ∫(3ex + 1) dx = 3ex + x + C
⟶ Chọn A
A.
B.
C.
D.
Hướng dẫn giải:
Ta có:
⟶ Chọn A
A.
B.
C.
D.
Hướng dẫn giải:
⟶ Chọn A
A.
B.
C.
D.
Hướng dẫn giải:
⟶ Chọn A
A.
B.
C.
D.
Hướng dẫn giải:
⟶ Chọn A
A.
B.
C.
D.
Hướng dẫn giải:
Đặt
⟶ Chọn A
A.
B.
C.
D.
Hướng dẫn giải:
Đặt
⟶ Chọn A
A.
B.
C.
D.
Hướng dẫn giải:
Đặt
Khi đó
⟶ Chọn A
A.
B.
C.
D.
Hướng dẫn giải:
Đặt
Khi đó
⟶ Chọn A
A.
B.
C.
D.
Hướng dẫn giải:
⟶ Chọn A
A.
B.
C.
D.
Hướng dẫn giải:
⟶ Chọn A
A.
B.
C.
D.
Hướng dẫn giải
⟶ Chọn A
A. –3
B. 3
C. 6
D.
Hướng dẫn giải:
⟶ Chọn A
A. F(x) = sin x – xcos x + C
B. F(x) = xsin x – cos x + C
C. F(x) = sin x + xcos x + C
D. F(x) = xsin x + xcos x + C
Hướng dẫn giải
Phương pháp tự luận: Sử dụng phương pháp nguyên hàm từng phần
Phương pháp trắc nghiệm:
Cách 1: Dùng định nghĩa, sử dụng máy tính nhập , CALC ngẫu nhiên tại một số điểm x0 thuộc tập xác định, kết quả xấp xỉ bằng 0 chọn.
Cách 2: Sử dụng phương pháp bảng
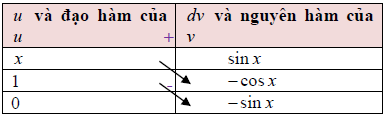
Vậy F(x) = sin x – xcos x + C
⟶ Chọn A
A.
B.
C.
D.
Hướng dẫn giải
Phương pháp tự luận: Sử dụng phương pháp nguyên hàm từng phần 2 lần.
Phương pháp trắc nghiệm
Cách 1: Sử dụng định nghĩa F’(x) = f(x) ⇔ F’(x) – f(x) = 0
Nhập máy tính . CALC x tại một số giá trị ngẫu nhiên x0 trong tập xác định, nếu kết quả xấp xỉ bằng 0 thì chọn.
Cách 2: Sử dụng phương pháp bảng:

Do đó
⟶ Chọn A
A.
B.
C.
D.
Hướng dẫn giải:
Phương pháp tự luận: Biến đổi rồi sử dụng phương pháp nguyên hàm từng phần.
Phương pháp trắc nghiệm:
Cách 1: Sử dụng định nghĩa F’(x) = f(x) ⇔ F’(x) – f(x) = 0
Nhập máy tính . CALC x tại một số giá trị ngẫu nhiên x0 trong tập xác định, nếu kết quả xấp xỉ bằng 0 thì chọn.
Cách 2: Sử dụng phương pháp bảng:
⟶ Chọn A
A.
B.
C.
D.
Hướng dẫn giải:
Phương pháp tự luận: Sử dụng phương pháp nguyên hàm từng phần với
Phương pháp trắc nghiệm:
Cách 1: Sử dụng định nghĩa F’(x) = f(x) ⇔ F’(x) – f(x) = 0
Nhập máy tính . CALC x tại một số giá trị ngẫu nhiên x0 trong tập xác định, nếu kết quả xấp xỉ bằng 0 thì chọn.
Cách 2: Sử dụng phương pháp bảng:
⟶ Chọn A
A. F(x) = x․tan x + ln|cos x| + C
B. F(x) = –x․cot x + ln|cos x| + C
C. F(x) = –x․tan x + ln|cos x| + C
D. F(x) = –x․cot x – ln|cos x| + C
Hướng dẫn giải:
Phương pháp tự luận: Sử dụng phương pháp nguyên hàm từng phần với
Phương pháp trắc nghiệm:
Cách 1: Sử dụng định nghĩa F’(x) = f(x) ⇔ F’(x) – f(x) = 0
Nhập máy tính . CALC x tại một số giá trị ngẫu nhiên x0 trong tập xác định, nếu kết quả xấp xỉ bằng 0 thì chọn.
Cách 2: Sử dụng phương pháp bảng:
⟶ Chọn A
A. F(x) = (x2 – 2) sin x + 2x cos x + C
B. F(x) = 2x2 sin x – x cos x + sin x + C
C. F(x) = x2 sin x – 2x cos x + 2sin x + C
D. F(x) = (2x + x2) cos x – x sin x + C
Hướng dẫn giải:
Phương pháp tự luận: Sử dụng phương pháp nguyên hàm từng phần 2 lần với u = x2; dv = cosx dx, sau đó u1 = x; dv1 = sinx dx
Phương pháp trắc nghiệm:
Cách 1: Sử dụng định nghĩa F’(x) = f(x) ⇔ F’(x) – f(x) = 0
Nhập máy tính . CALC x tại một số giá trị ngẫu nhiên x0 trong tập xác định, nếu kết quả xấp xỉ bằng 0 thì chọn.
Cách 2: Sử dụng phương pháp bảng:
⟶ Chọn A
A.
B.
C.
D.
Hướng dẫn giải:
Phương pháp tự luận: Sử dụng phương pháp nguyên hàm từng phần với u = x; dv = sin2x dx
Phương pháp trắc nghiệm:
Sử dụng phương pháp bảng hoặc sử dụng máy tính:
Nhập , CALC ngẫu nhiên tại một số điểm x0 bất kỳ, nếu kết quả xấp xỉ bằng 0 thì chọn đáp án đó.
⟶ Chọn A
A. f(x = x․cos x
B. f(x) = x․sin x
C. f(x) = –x․cos x
D. f(x) = –x․sin x
Hướng dẫn giải:
Phương pháp tự luận: Tính F’(x) có kết quả trùng với đáp án chọn.
Phương pháp trắc nghiệm:
Sử dụng định nghĩa F’(x) = f(x) ⇔ F’(x) – f(x) = 0
Nhập máy tính . CALC x tại một số giá trị ngẫu nhiên x0 trong tập xác định, nếu kết quả xấp xỉ bằng 0 thì chọn
⟶ Chọn A
A.
B.
C.
D.
Hướng dẫn giải:
Phương pháp tự luận: Sử dụng phương pháp nguyên hàm từng phần với u = 1 + ln (x + 1); hoặc biến đổi rồi đặt u = ln (x + 1);
Phương pháp trắc nghiệm: Sử dụng máy tính kiểm tra bằng định nghĩa.
Câu 35: Trong các mệnh đề sau mệnh đề nào nhận giá trị đúng?
A. Hàm số y = 1/x có nguyên hàm trên (-∞; +∞).
B. 3x2 là một số nguyên hàm của x3 trên (-∞; +∞).
C. Hàm số y = |x| có nguyên hàm trên (-∞;+∞).
D. 1/x + C là họ nguyên hàm của lnx trên (0;+∞).
Dựa vào định lí: Mọi hàm số liên tục trên K đều có nguyên
hàm trên K. Vì y = |x| liên tục trên R nên có nguyên hàm trên R .
Phương án A sai vì y=1/x không xác định tại x=0 ∈ (-∞;+∞).
Phương án B sai vì 3x2 là đạo hàm của x3.
Phương án D sai vì 1/x là đạo hàm của lnx trên (0; +∞).
Vậy chọn đáp án C.
Câu 36: Hàm số nào dưới đây không phải là một nguyên hàm của f(x)=2x-sin2x ?
x2 + (1/2).cos2x B. x2 + cos2 x C. x2 - sin2x D. x2 + cos2x .
Ta có
∫(2x-sin2x)dx=2∫xdx-∫sin2xdx

D không phải là nguyên hàm của f(x). Vậy chọn đáp án D.
Câu 37: Tìm nguyên hàm của
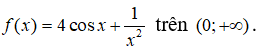
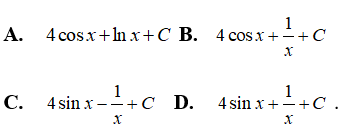
Với x ∈ (0; +∞) ta có
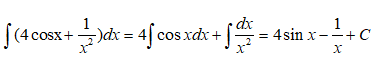
Vậy chọn đáp án C.
Câu 38:
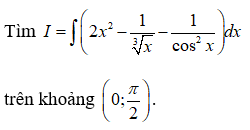
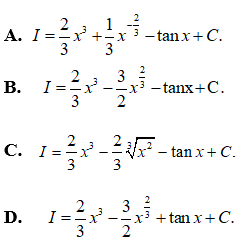
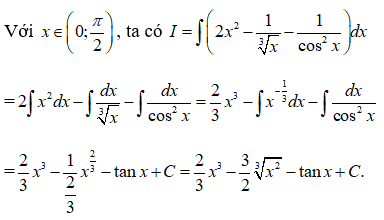
Vậy chọn đáp án B.
Câu 39:
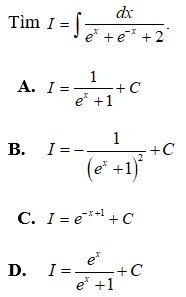
Đặt u = ex + 1 ⇒ u' = ex. Ta có
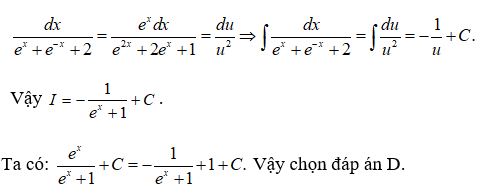
Câu 40: Trong các hàm số sau hàm số nào không phải là một nguyên hàm của f(x) = cosxsinx ?
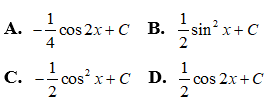
Sử dụng phương pháp biến đổi số ta có:
Đặt u = cosx thì u’ = -sinx và ∫sinxcosxdx = -∫u.u'dx = -∫udu
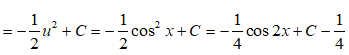
Câu 41: Tìm I=∫(3x2 - x + 1)exdx
A. I = (3x2 - 7x +8)ex + C B. I = (3x2 - 7x)ex + C
C. I = (3x2 - 7x +8) + ex + C D. I = (3x2 - 7x + 3)ex + C
Sử dụng phương pháp tính nguyên hàm từng phần ta có:
Đặt u = 3x2 - x + 1 và dv = exdx ta có du = (6x - 1)dx và v = ex . Do đó:
∫(3x2 - x + 1)exdx = (3x2 - x + 1)ex - ∫(6x - 1)exdx
Đặt u1 = 6x - 1; dv1 = exdx Ta có: du1 = 6dx và v1 = ex .
Do đó ∫(6x - 1)exdx = (6x - 1)ex - 6∫exdx = (6x - 1)ex - 6ex + C
Từ đó suy ra
∫(3x2 - x + 1)exdx = (3x2 - x + 1)ex - (6x - 7)ex + C = (3x2 - 7x + 8)ex + C
Vậy chọn đáp án A.
Câu 41: Một vật chuyển động với vận tốc v(t) (m/s) có gia tốc
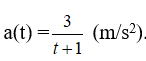
Vận tốc ban đầu của vật là 6m/s. Vận tốc của vật sau 10 giây xấp xỉ bằng
A. 10m/s B. 11m/s C. 12m/s D. 13m/s.
Vận tốc của vật bằng
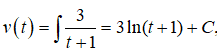
với t = 0 ta có v(0)= C = 6 nên phương trình vận tốc của chuyển động là :
v(t) = 3ln(t + 1) + 6 (m/s)
khi đó v(10) = 3ln11 + 6 ≈ 13 (m/s) .
Vậy chọn đáp án D.
Câu 42: Tìm I = ∫cos(4x + 3)dx .
A. I = sin(4x + 2) + C B. I = - sin(4x + 3) + C
C. I = (1/4).sin(4x + 3) + C D. I = 4sin(4x + 3) + C
Đặt u = 4x + 3
⇒ du = 4dx ⇒ dx = 1/4 du và cos(4x+3)dx được viết thành
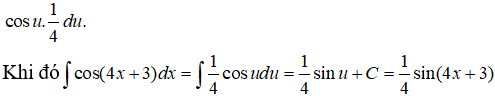
Câu 43: Họ nguyên hàm của hàm số f(x) = (2 tanx + cotx)2 là:
A. 2tanx - cotx - x + C B. 4tanx + cotx - x + C
C. 4tanx - cotx + x + C D. 4tanx - cotx - x + C
∫(2tanx + cotx)2dx = ∫(4tan2x + 2tanx.cotx + cot2x)dx
= ∫ [4(tan2x + 1) + (cot2x + 1) - 1]dx
= 4tanx = cotx - x + C
Câu 44: Biết rằng: f'(x) = ax + b/x2, f(-1) = 2, f(1) = 4, f'(1) = 0
Giá trị biểu thức ab bằng :
A.0 B.1 C.-1 D. 1/2 .
Ta có:
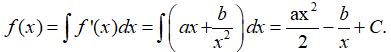
Từ điều kiện đã cho ta có phương trình sau:
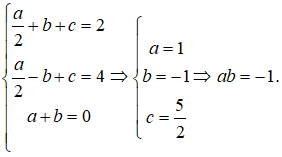
Câu 45: Một đám vi khuẩn tại ngày thứ t có số lượng là N(t). Biết rằng
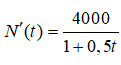
và lúc đầu đám vi khuẩn có 250000 con. Sau 10 ngày số lượng vi khuẩn xấp xỉ bằng:
A. 264334 B. 263334 C.264254 D.254334.
Số lượng vi khuẩn tại ngày thứ t bằng
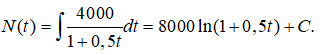
Với t = 0 ta có: N(0) = 250000,
Vậy N(t) = 8000.ln(1 + 0,5t) + 250000
khi đó N(10) ≈ 264334.
Câu 46:
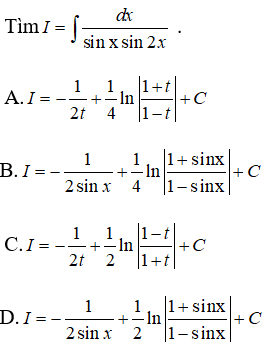
Ta biến đổi để thu được:
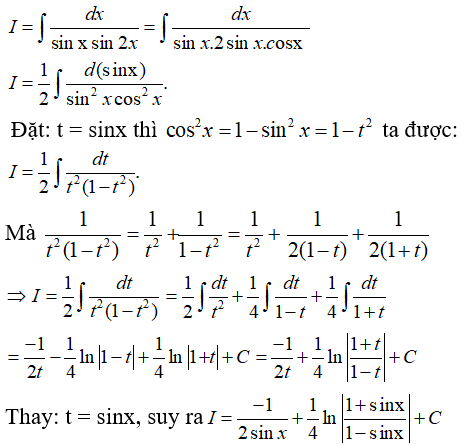
Câu 47.Tìm nguyên hàm của hàm số f(x) = 22x.3x.7x .
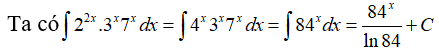
Câu 48: Họ nguyên hàm của hàm số
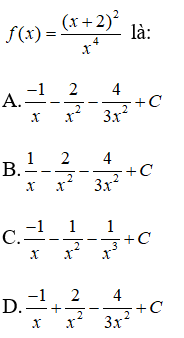
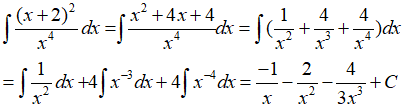
Câu 49: Họ nguyên hàm của hàm số
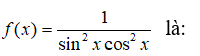
A. cot2x + C B. -2cot2x + C C. 2cot2x + C D. -cot2x + C
.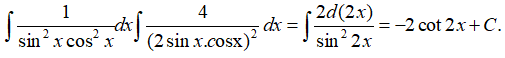
Câu 50: Tìm I = ∫sin5xcosxdx .
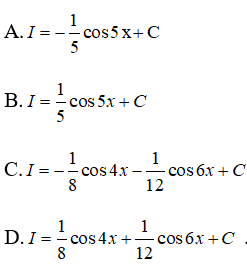
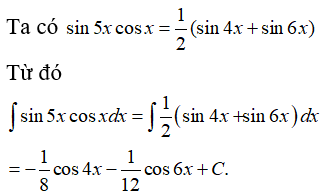
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.