Phương trình bậc hai với hệ số thực (Lý thuyết + 50 bài tập có lời giải)

A. Tóm tắt lý thuyết

1. Căn bậc hai của số phức: Cho số phức w. Mỗi số phức z thỏa mãn z² = w được gọi là một căn bậc hai của w .

2. Phương trình bậc hai với hệ số thực:

    Cho phương trình bậc hai ax² + bx + c = 0 (a, b, c ∈ R; a ≠ 0). Xét Δ = b² - 4ac, ta có

    • Δ = 0: phương trình có nghiệm thực x = -b/2a .

    • Δ > 0 : phương trình có hai nghiệm thực được xác định bởi công thức: .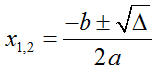

    • Δ < 0 : phương trình có hai nghiệm phức được xác định bởi công thức: .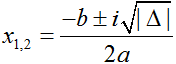

    ** Chú ý.

    - Mọi phương trình bậc n: A₀zⁿ + A₁z^n-1 + ... + A_n-1z + A_n = 0 luôn có n nghiệm phức (không nhất thiết phân biệt).

    -Hệ thức Vi–ét đối với phương trình bậc hai với hệ số thực: Cho phương trình bậc hai ax²+ bx + c = 0 (a ≠ 0) có hai nghiệm phân biệt x₁, x₂(thực hoặc phức). Ta có hệ thức Vi–ét

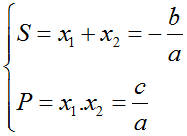
B. Bài tập

Câu 1: Phương trình z² -az + b = 0 (a, b ∈ R) có nghiệm z = 1 + i khi

A. a = 2, b = -2    

B. a = 2, b = 2    

C. a = -2, b = 2   

D. a = -2, b = -2

Thay z = 1 + i vào phương trình đã cho ta có:

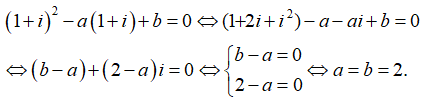
Chọn đáp án B

Câu 2: Phương trình 2z² + 4z + 5 = 0 có các nghiệm là

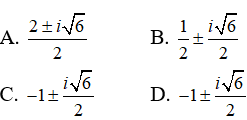
Ta có: Δ' = 4 - 10 = -6 = 6i²

Phương trình đã cho có các nghiệm là

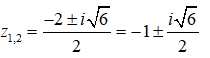
Chọn đáp án C

Câu 3: Phương trình z² - z + 1 = 0 có hai nghiệm là

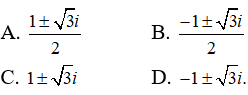
Ta có: Δ = 1² - 4 = -3 = 3i²

Các nghiệm của phương trình đã cho là

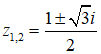
Chọn đáp án A

Câu 4: Để phương trình z² + bz + c = 0 nhận z₁ = -4 + 2i và z₂ = -4 - 2i làm nghiệm thì

A. b = -8, c = 20   

B. b = -8, c = -20

C. b = 8, c = 20    

D. b = 8, c = 20

Gọi z₁, z₂ là hai nghiệm của phương trình đã cho, áp dụng hệ thức Vi-ét ta có:

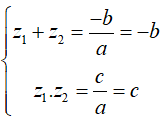
Để phương trình đã cho nhận z₁, z₂ làm nghiệm thì

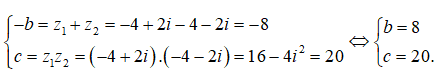
Chọn đáp án D

Câu 5: Phương trình z² + 6z + 15 = 0 có các nghiệm là z₁, z₂.Giá trị biểu thức T = |z₁| + |z₂| bằng:

A. 2√15    

B. 6   

C. 4√5   

D. 2√3

Ta có:Δ' = 9 - 15 = -6 = 6i²

Các nghiệm của phương trình là z₁ = - 3 - i√6, z₂ = - 3 + i√6

Do đó

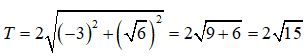
Chọn đáp án A

Câu 6: Phương trình z₁ = 1 + 2i, z₂ = 2 - 3i có nghiệm là z = 2 + i khi

A. a = 1, b = 4   

B. a = -1, b = 4   

C. a = -1, b = -4    

D. a = 1, b = -4

Thay z = 2 + i vào phương trình đã cho ta có:

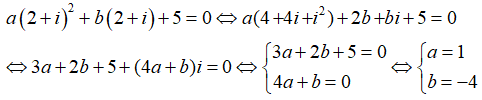
Chọn đáp án D

Câu 7: Phương trình (1 + i)² = -7 + i có các nghiệm là

A. -1 - 2i và 1 + 2i   

B. -1 + 2i và 1 + 2i

C. -1 + 2i và 1 - 2i    

D. 1 + 2i và 1 - 2i

Phương trình đã cho tương đương với

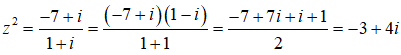
Viết -3 + 4i = 4i² + 4i + 1 = (2i + 1)², ta có: z² = (2i + 1)² <=> z = ±(2i + 1)

Chú ý: Nếu việc viết -3 + 4i = (2i + 1)² gặp khó khăn thì có thể đặt z = a + bi (a, b ∈ R). Ta có :

(a + bi)² = -3 + 4i <=> a² - b² + 2abi = -3 + 4i

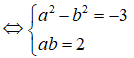
Từ phương trình thứ hai của hệ ta có b = 2/a

Thay vào phương trình thứ nhất của hệ ta có

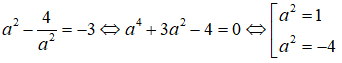
Vì a ∈ R và a² ≥ 0 nên a² = 1 hay a = ±1 . Từ đó ta có hai nghiệm : z₁ = -1 - 2i và z₂ = 1 + 2i

Chọn đáp án A

Câu 8: Phương trình z² + 4x + 5 = 0 có các nghiệm là

A. 2 ± i   

B. -2 ± i   

C. 4 ± i   

D. -4 ± i

Ta có: Δ' = 2² - 1.5 = -1 = i². Phương trình có hai nghiệm là:

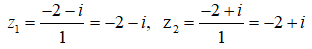
Chọn đáp án B

Câu 9: Phương trình z² + 8z + 17 = 0 có hai nghiệm

A. 1 - i và 1 - 2i    

B. 4 - i và 4 + i

C. -4 - i và -4 + i    

D. -2 + 2i và -2 + 4i

Ta có: Δ = 16 - 17 = -1 = i². Phương trình có các nghiệm là:

z₁ = -4 - i, z₂ = -4 + i

Chọn đáp án C

Câu 10: Phương trình z² - 4z + 9 = 0 có hai nghiệm. Giá trị biểu thức T = |z₁| + |z₂| bằng

A. – 6   

B. 6   

C. 8   

D. 2√3

Ta có: Δ' = 4 - 9 = -5 = 5i². Phương trình có hai nghiệm là:

z_1,2 = 2 ± i√5

Vậy T = 2√(4 + 5) = 2√9 = 6

Chọn đáp án B

Câu 11: Phương trình z⁴ + 3z² - 4 = 0 có 4 nghiệm phức z₁, z₂, z₃, z₄. Giá trị biểu thức T = |z₁| + |z₂| + |z₃| + |z₄| bằng

A. 6    

B. 2√2   

C. 2 + 2√2   

D. 4 + 2√2

Ta có

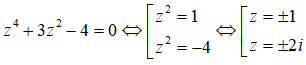
⇒ |z₁| = |z₂| = 1; |z₃| = |z₄| = 2

Vậy T = 1 + 1 + 2 + 2 = 6

Chọn đáp án A

Câu 12: Số phức z thỏa mãn

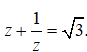
Giá trị biểu thức

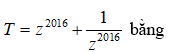
A. 1    

B. 2   

C. 3    

D. 3⁶⁷²

Ta có: z + 1/z = √3 <=> z² - √3z + 1 = 0 (1)

Xét phương trình (1): Ta có: Δ = (√3)² - 4.1.1 = -1 = i²

Phương trình (1) có hai nghiệm là:

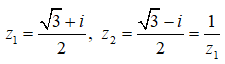
Do đó

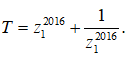
Ta có:

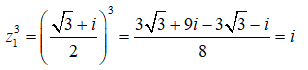
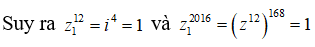
Vậy T = 1 + 1 = 2

Chọn đáp án B

Câu 13:Trong C , phương trình |z| + z = 2 + 4i có nghiệm là:

A. z = -3 + 4i         B. z = -2 + 4i

C. z = -4 + 4i         D. z = -5 + 4i

Đáp án : A

Giải thích :

Đặt z = a + bi khi đó |z| = 

Thay vào phương trình: 

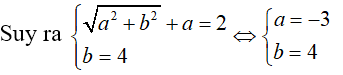
Câu 14:Hai giá trị x₁ = a + bi ; x₂ = a - bi là hai nghiệm của phương trình nào :

A. x² + 2ax + a² + b² = 0        B. x² + 2ax + a² - b² = 0

C. x² - 2ax + a² + b² = 0        D. x² - 2ax + a² - b² = 0

Đáp án : C

Giải thích :

Áp dụng định lý đảo Viet :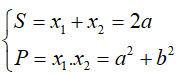 

Do đó x₁ ; x₂ là hai nghiệm của phương trình:

x² - Sx + P = 0 hay . x² - 2ax + a²+ b² = 0

Câu 15: Trong C , nghiệm của phương trình z² + 4z + 5 = 0 là:

Đáp án : C

Giải thích :

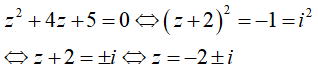
Câu 16:Trong C , nghiệm của phương trình z² - 2z + 1 - 2i = 0 là

Đáp án : D

Giải thích :

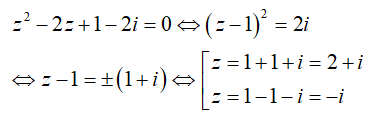
Câu 17:Trong C , phương trình z³ + 1 = 0 có nghiệm là:

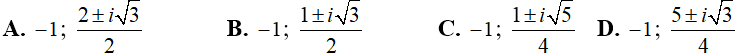
Đáp án : B

Giải thích :

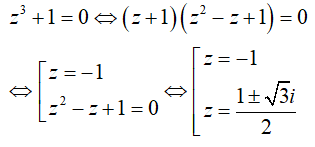
Câu 18: Trong C , phương trình z⁴ - 1 = 0 có nghiệm là:

A ±1;±2i        B. ±2;±2i        C. ±3; ±4i        D. ±1;±i

Đáp án : D

Giải thích :

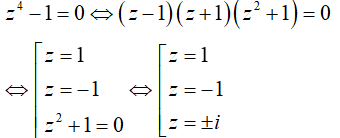
Câu 19:Phương trình z³ = 8 có bao nhiêu nghiệm phức với phần ảo âm?

A. 1        B. 2        C. 3        D. 0

Đáp án : A

Giải thích :

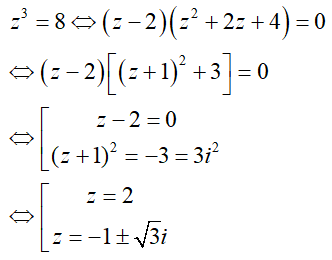
Do đó phương trình chỉ có một nghiệm phức có phần ảo âm.

Câu 20: Phương trình sau có mấy nghiệm thực: z² + 2z + 2 = 0

A. 0        B. 1        C. 2        D. 3

Đáp án : A

Giải thích :

Ta có:

nên phương trình vô nghiệm trên tập số thực.

Câu 21: Trong C , phương trình z⁴ + 4 = 0 có nghiệm là:

Đáp án : D

Giải thích :

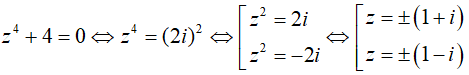
Câu 22:Tập nghiệm trong C của phương trình z³ + z² + z + 1 = 0 là:

A. {-i ; i ; 1 ; -1}         B. {-i ; i ; 1 }        C. {-i ; -1}         D . {-i ; i ; -1}

Đáp án : A

Giải thích :

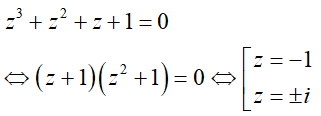
Câu 23:Trên tập số phức, phương trình bậc hai có hai nghiệm 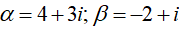 là:

Đáp án : B

Giải thích :

Áp dụng định lý Viet, ta có:  .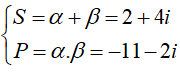

Do đó α,β là hai nghiệm của phương trình:

z² - Sz + P = 0 <=> z² - (2 + 4i)z - (11 + 2i) = 0

Câu 24: Phương trình (2 + i) z² + az + b = 0 có hai nghiệm là 3 + i và 1 - 2i. Khi đó a = ?

A. -9 - 2i        B. 15 + 5i        C. 9 + 2i        D. 15 - 5i

Đáp án : A

Giải thích :

Theo Viet, ta có:

(3 + i) + (1 - 2i) = 4 - i

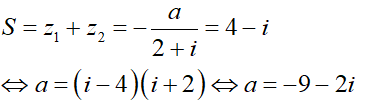
Câu 25:Giá trị của các số thực b, c để phương trình z² + bz + c = 0 nhận số phức z = 1 + i làm một nghiệm là:

Đáp án : C

Giải thích :

Do z = 1 + i là một nghiệm của phương trình đã cho nên ta có:

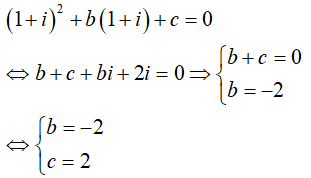
Câu 26:Trên tập hợp số phức, phương trình z² + 7z + 15 = 0 có hai nghiệm z₁;z₂. Giá trị biểu thức z₁ + z₂ + z₁z₂ là:

A. –7        B. 8        C. 15        D. 22

Đáp án : B

Giải thích :

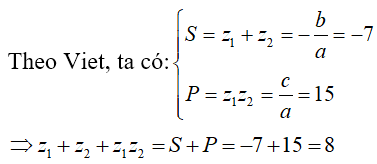
Câu 27:Trên tập số phức, cho phương trình sau: (z + i)⁴ + 4z² = 0 . Có bao nhiêu nhận xét đúng trong số các nhận xét sau?

1. Phương trình vô nghiệm trên trường số thực R .

2. Phương trình vô nghiệm trên trường số phức C .

3. Phương trình không có nghiệm thuộc tập số thực.

4. Phương trình có bốn nghiệm thuộc tập số phức.

5. Phương trình chỉ có hai nghiệm là số phức.

6. Phương trình có hai nghiệm là số thực

A. 0        B. 1        C. 3        D. 2

Đáp án : D

Giải thích :

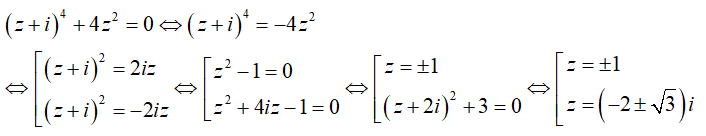
Do đó phương trình có 2 nghiệm thực và 4 nghiệm phức. Vậy nhận xét 4, 6 đúng.

Câu 28:Giả sử z₁;z₂ là hai nghiệm của phương trình z² - 2z + 5 = 0 và A, B là các điểm biểu diễn của z₁;z₂ . Tọa độ trung điểm I của đoạn thẳng AB là:

A.I(1;1)        B.I(-1;0)        C. I(0;1)        D.I(1;0)

Đáp án : D

Giải thích :

z² - 2z + 5 = 0 <=> (z-1)² + 4 = 0 <=> z = 1 ± 2i

=> A (1;2); B (1;-2)

Do đó tọa độ trung điểm I của đoạn thẳng AB là I(1;0).

Câu 29:Trong tập số phức, giá trị của m để phương trình bậc hai z² + mz + i = 0 có tổng bình phương hai nghiệm bằng -4i là:

A.±(1-i)        B.1-i        C.±(1+i)        D. -1-i

Đáp án : A

Giải thích :

Gọi z₁;z₂ là hai nghiệm của phương trình.

Theo Viet, ta có: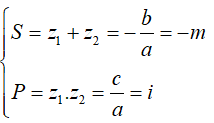 

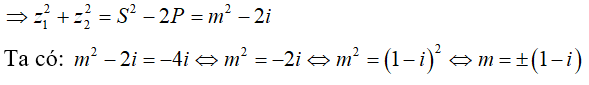
Câu 30:Cho phương trình z² - mz + 2m - 1 = 0 trong đó m là tham số phức. Giá trị của m để phương trình có hai nghiệm z₁;z₂ thỏa mãn z₁² + z₂² = 10 là:

A. m = 2 ± 2√2i        B. m = 2 + 2√2i         C. m = 2 - 2√2i         D. m = -2 - 2√2i

Đáp án : A

Giải thích :

Theo Viet, ta có: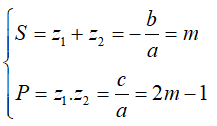 

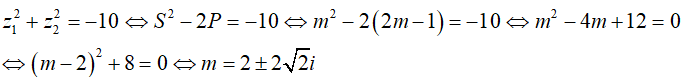
Câu 31: Gọi z₁;z₂ là hai nghiệm của phương trình z² + 2z + 8 = 0, trong đó z₁ có phần ảo dương. Giá trị của số phức  là:

A. 12 + 6i    B. 10    C. 8        D. 12 - 6i

Đáp án : C

Giải thích :

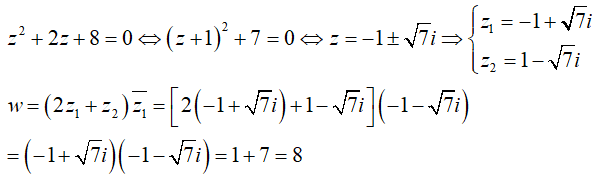
Câu 32: Gọi z₁;z₂ là hai nghiệm của phương trình z² - 2z + 6 = 0. Trong đó z₁ có phần ảo âm. Giá trị biểu thức M = |z₁| + |3z₁ - z₂| là:

Đáp án : A

Giải thích :

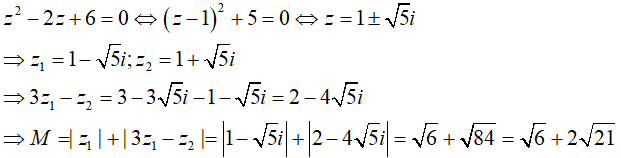
Câu 33:Phương trình x⁴ + 2x² - 24x + 72 = 0 trên tập số phức có các nghiệm là:

Đáp án : A

Giải thích :

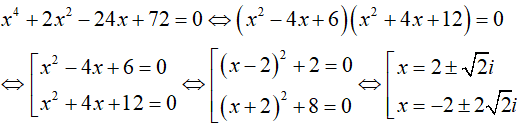
Câu 34:Trong C, phương trình 2x² + x + 1 = 0 có nghiệm là:

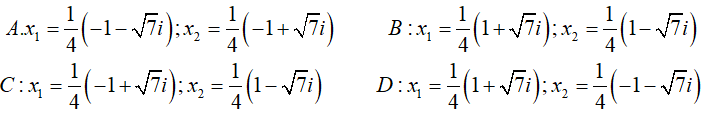
Đáp án : A

Giải thích :

Ta có:Δ = b² - 4ac = 1² - 4.1.1 = -7 = 7i² <0

nên phương trình có hai nghiệm phức là:

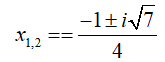
Câu 35:Trong C , phương trình z² - z + 1 = 0 có nghiệm là:

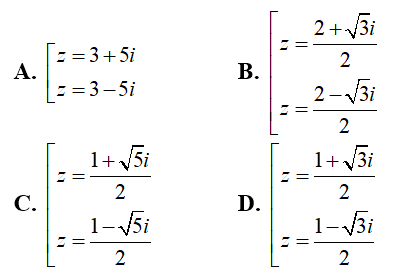
Đáp án : D

Giải thích :

Δ = b² - 4ac = -3 < 0

Nên phương trình có hai nghiệm phức là:

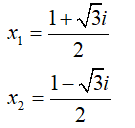
Câu 36:Trong C , nghiệm của phương trình z² = -5 + 12i là:

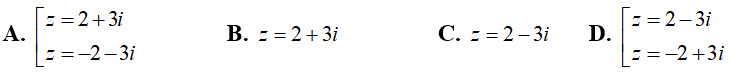
Câu 37: Trong C , phương trình z⁴-6z² + 25 = 0 có nghiệm là:

Đáp án : D

Giải thích :

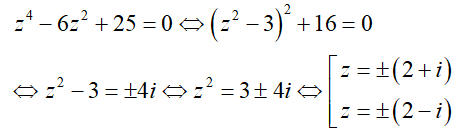
Câu 38:Biết z₁;z₂ là hai nghiệm của phương trình z² + √3 z + 3 = 0. Khi đó giá trị của z₁² + z₂² là:

Đáp án : D

Giải thích :

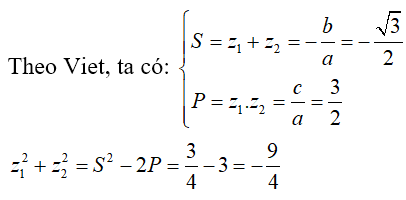
Câu 39: Phương trình z² + az + b = 0 có một nghiệm phức là z = 1 + 2i. Tổng 2 số a và b bằng:

A. 0        B.        C. 3        D. -1

Đáp án : C

Giải thích :

Vì z = 1 + 2i là một nghiệm của phương trình z² + az + b = 0 nên ta có:

(1 + 2)² + a(1 + 2i) + b = 0

<=> a + b + 2ai = 3 - 4i

<=> a + b = 3

Câu 40:Gọi z₁;z₂ là hai nghiệm phức của phương trình z² - 4z + 5 = 0. Khi đó phần thực của z₁² + z₂² là:

A. 5        B. 6        C. 4        D. 7

Đáp án : B

Giải thích :

Theo Viet, ta có: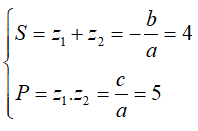 

Câu 41:Gọi z₁;z₂ là hai nghiệm phức của phương trình z² + 2z + 4 = 0. Khi đó A = |z₁|² + |z₂|² có giá trị là

A.-7         B. – 8         C.-4        D. 8

Đáp án : D

Giải thích :

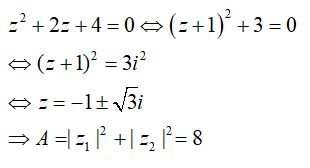
Câu 42: Cho số phức z thỏa mãn z² - 6z + 13 = 0. Tính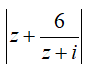 

A. √17 và 4        B. √17 và 5        C. √17 và 3        D. √17 và 2

Đáp án : B

Giải thích :

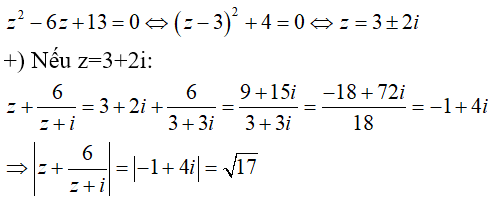
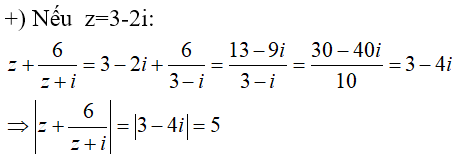
Câu 43: Gọi z₁;z₂ là các nghiệm phức của phương trình z² + (1-3i)z - 2(1+i) = 0. Khi đó w = z₁² + z₂² - 3 z₁z₂ là số phức có môđun là:

A.5        B.√13        C. 2√13        D. √20

Đáp án : D

Giải thích :

Theo Viet, ta có: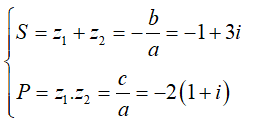 

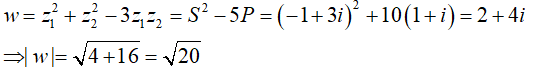
Câu 44: Số nghiệm của phương trình với ẩn số phức z: 4z² + 8|z|² -3 = 0 là:

A. 3        B. 2        C. 4        D. 1

Đáp án : C

Giải thích :

Gọi z = a + bi là nghiệm của phương trình.

Ta có:

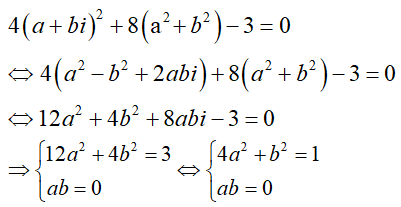
Vậy phương trình có 4 nghiệm phức

Câu 45: Cho phương trình z² + mz - 6i = 0. Để phương trình có tổng bình phương hai nghiệm bằng 5 thì m = +(a + bi) (a,b ∈ R) có dạng . Giá trị a+2b là:

A. 0         B. 1        C. -2        D. -1

Đáp án : D

Giải thích :

Gọi z₁;z₂ là hai nghiệm của phương trình đã cho

Theo Viet, ta có: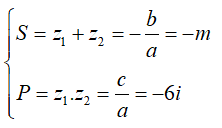 

Theo bài cho, tổng bình phương hai nghiệm bằng 5. Ta có:

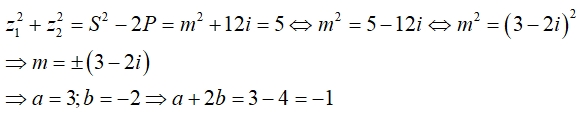
Câu 46:Gọi z₁;z₂;z₃;z₄ là các nghiệm phức của phương trình 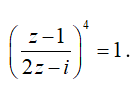 Giá trị củ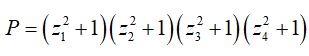a  là :

Đáp án : B

Giải thích :

Với mọi 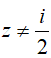 , ta có:

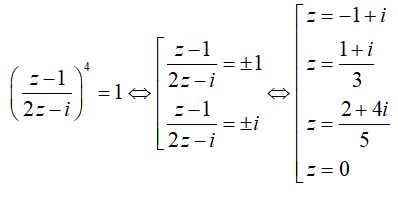
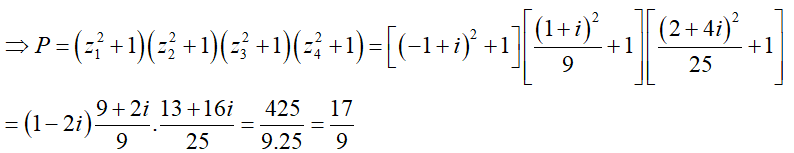 Câu 47:Tìm các căn bậc hai của w = -5 + 12i.

Gọi z = x + yi là một căn bậc hai của số phức w = -5 + 12i

Ta có z² = w <=> (x + yi)² = -5 + 12i

<=> 

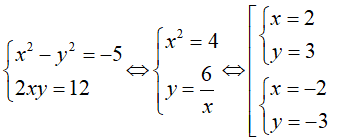
Vậy số phức w có hai căn bậc hai là 2 + 3i và -2 - 3i.

Câu 48:Tính căn bậc hai của số phức z = 8 + 6i ra kết quả:

Giả sử w = x + yi là một căn bậc hai của số phức z = 8 + 6i.

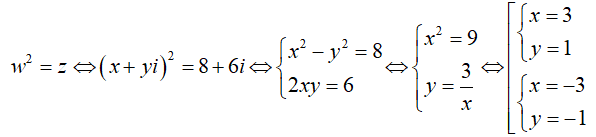
Ta có:

Do đó z có hai căn bậc hai là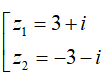 

Chọn đáp án A.

Câu 49: Cho z = 3 + 4i. Tìm căn bậc hai của z.

A. -2 + i và 2 - i         B. 2 + i và 2 - i

C. 2 + i và -2 - i         D. 3 - 2i và 2 - 3i

Hướng dẫn:

Giả sử w = x + yi là một căn bậc hai của số phức z = 3 + 4i.

Ta có:

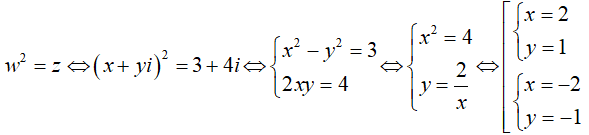
Do đó z có hai căn bậc hai là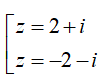 

Chọn đáp án A.

Câu 50: Căn bậc hai của số phức 4 + 6√5i là:

A.-(3 + √5i)        B.(3 + √5i)         C.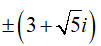         D. 2

Giả sử w là một căn bậc hai của 4 + 6√5i. Ta có:

Chọn đáp án A.