1. Phần thực và phần ảo của số phức, số phức liên hợp.
a) Số phức z là biểu thức có dạng z = a + bi (a, b ∈ R, i2 = -1) . Khi đó:
+ Phần thực của z là a, phần ảo của z là b và i được gọi là đơn vị ảo.
b) Số phức liên hợp của z là 
.
+ Tổng và tích của z và z− luôn là một số thực.
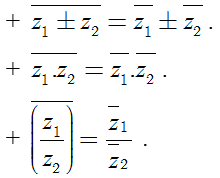
Đặc biệt:
+ Số phức z = a + 0i có phần ảo bằng 0 được coi là số thực và viết là z = a
+ Số phức z = 0 + bi có phần thực bằng 0 được gọi là số ảo (hay số thần ảo) và viết là
+ Số i = 0 + li = li.
+ Số: 0 = 0 + 0i vừa là số thực vừa là số ảo.
2. Số phức bằng nhau.
+ Cho hai số phức z1 = a1 + b1i, z2 + b2i (a1, a2, b1, b2 ∈ R). Khi đó:
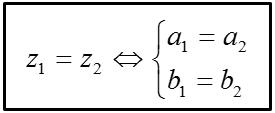
3. Biểu diễn hình học của số phức, mô đun của số phức.
a) Biễu diễn hình học của số phức.
+ Số phức z = a + bi (a, b ∈ R) được biểu diễn bởi điểm M(a; b) trong mặt phẳng tọa độ.
+ z và z− được biểu diễn bởi hai điểm đối xứng nhau qua trục 0x.
b) Mô đun của số phức.
+ Mô đun của số phức z là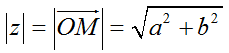 
.
+ 
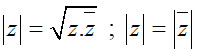
B. Bài tập
Câu 1:Cho số phức z = 5 - 4i. Môđun của số phức z là
A.3 B.√41. C. 1. D. 9.
Đáp án : B
Giải thích :
+z = 5 - 4i có a = 5; b = -4
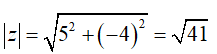
Câu 2:Cho số phức z = 5 - 6i. Số phức liên hợp của z là
A. z = 5 + 6i B.z = -5 + 6i C.z = -5 - 6i D.z = 6 - 5i
Đáp án : A
Giải thích :
Với z = 5 - 6i thì số phức liên hợp của z là:
z = 5 + 6i
Câu 3:Cho hai số phức z1 = 1 + 2i; z2 = 2 - 3i . Phần ảo của số phức w = 3z1 - 2z2 là
A. 12. B. 11. C. 1. D.12i
Đáp án : A
Giải thích :
w = 3z1 - 2z2 = 3(1 + 2i) - 2(2 - 3i) = 3 + 6i - 4 + 6i = -1 + 12i
Vậy phần ảo của số phức z là .
Câu 4: Số phức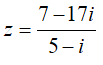 
có phần thực là
A. 2. B. 
. C. 3. D. -3 .
Đáp án : A
Giải thích :
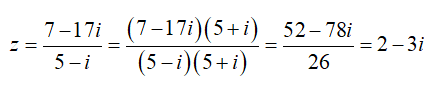
=> phần thực của z là 2
Câu 5: Cho số phức z = 3 + 4i. Khẳng định nào sau đây là khẳng định sai?
A. Điểm biểu diễn của z là M(3;4).
B. Môđun của số phức z là 5.
C. Số phức đối của z là -3 - 4i.
D. Số phức liên hợp của z là 3 - 4i.
Đáp án : A
Giải thích :
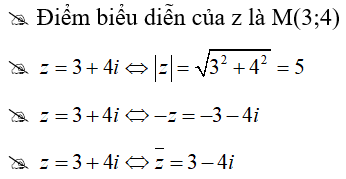
Câu 6:Số nào trong các số phức sau là số thuần ảo?
Đáp án : C
Giải thích :
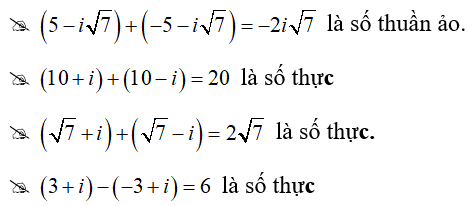
Câu 7:Cho số phức z = 1 + i. Khẳng định nào sau đây là khẳng định đúng?
A. 
= -1 + i . B. z-1z . C.|z|=2 D. z2 = 2i.
Đáp án : D
Giải thích :
Câu 8:Phần thực, phần ảo của số phức z thỏa mãn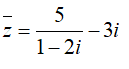 
lần lượt là
A. 1;1. B.1;-2 C. 1;2. D.1;-1
Đáp án : A
Giải thích :
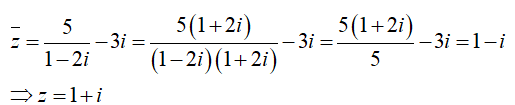
Phần thực, phần ảo của z lần lượt là 1;1.
Câu 9: Cho số phức z thỏa mãn điều kiện:(1 + i)
- 1 - 3i = 0. Phần ảo của số phứcw = 1 - iz + z là
A. 1. B. -3. C. -2. D. -1.
Đáp án : B
Giải thích :
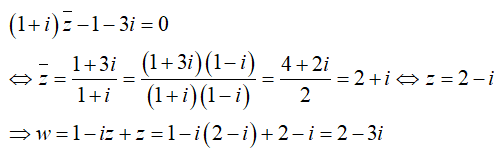
Phần ảo của w là -3
Câu 10: Cho z = 1 - 2i và w = 2 + i. Khẳng định nào sau đây là khẳng định sai?
Đáp án : A
Giải thích :
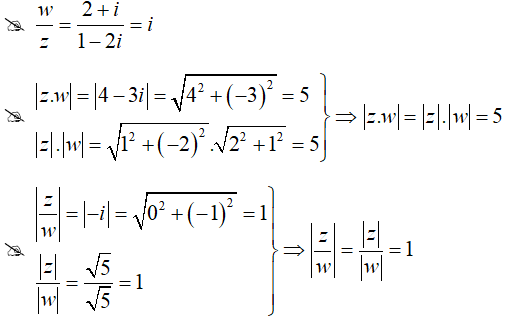
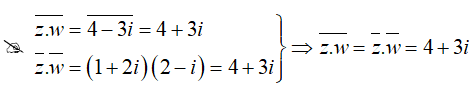
Câu 11:Tìm phần thực, phần ảo của số phức z thỏa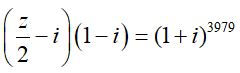 
A. Phần thực là 21990 và phần ảo là 2.
B. Phần thực là -21990 và phần ảo là 2.
C. Phần thực là -21989 và phần ảo là 1.
D. Phần thực là 21989 và phần ảo là 1
Đáp án : B
Giải thích :
Ta có:
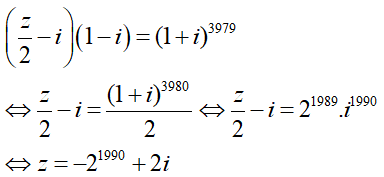
Câu 12:Cho số phức z thỏa . Khi đó phần thực và phần ảo của z = 1 + i + i2 + i3 + ... + i2016 lần lượt là
A.0 và -1. B. 0 và 1. C. 1 và 1. D. 1 và 0.
Đáp án : D
Giải thích :
Số phức z là tổng của cấp số nhân với số hạng đầu là 1 và công bội q = i . Do đó :
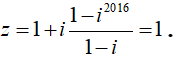
Câu 13:Giá trị của biểu thức S = 1 + i2 + i4 + ... + i4k , k ∈ N* là
A. 1. B. 0. C.2 D.ik
Đáp án : A
Giải thích :
Ta có nhận xét sau :
i2n + i2n + 2 = i2n(1 + i2) = 0, n ∈ N*
Áp dụng tính được
Câu 14:Cho số phức z = 1 + (1 + i) + (1 + i)2 + ...+ (1 + i)26 . Phần thực của số phức z là
A. 213 B. -(1 + 213) C. -213 D. (1 + 213)
Đáp án : A
Giải thích :
Số phức z là tổng của cấp số nhân với số hạng đầu là 1 và công bội q = 1 + i. Do đó :
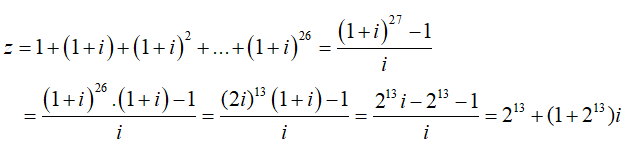
Vậy phần thực là 213
Câu 15: Cho số phức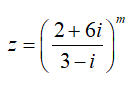 
,m nguyên dương. Có bao nhiêu giá trị m ∈ [1;50] để z là số thuần ảo?
A. 26. B. 25. C. 24. D. 50.
Đáp án : B
Giải thích :
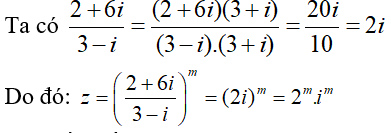
Z là số thuần ảo khi và chỉ khi m = 2k + 1
Mà
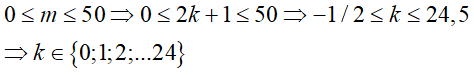
Với 25 giá trị của k cho ta tương ứng 25 giá trị m thỏa yêu cầu đề bài.
Câu 16:Cho số phức z = x + y.i thỏa mãn z3 = 2 - 2i. Cặp số là(x;y)
A.(2; 2) B.(1;1) .
C.(3;-3) D.(2; -3)
Đáp án : B
Giải thích :
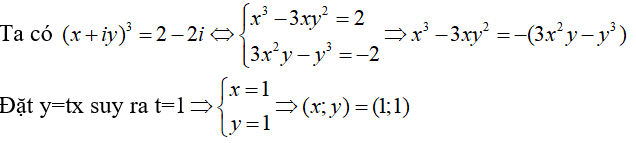
Câu 17:Cho biểu thức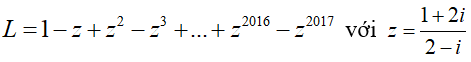 
. Biểu thức có giá tri là
Đáp án : A
Giải thích :
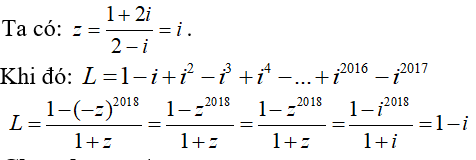
Câu 18:Cho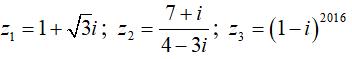 
. Tìm dạng đại số của 
Đáp án : B
Giải thích :
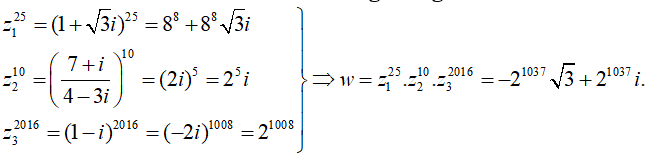
Câu 19:Cho số phức Tìm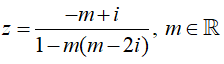 
|z|max
A. 
. B. 0. C. 1. D. 2.
Đáp án : A
Giải thích :
Ta có:
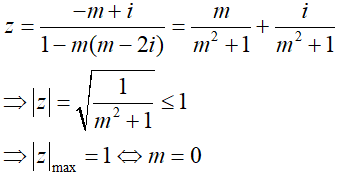
Câu 20:Cho hai số phức z1 = 1 + 2i ; z2 = 2 - 3i. Khẳng định nào sau đây là khẳng định sai?
Đáp án : C
Giải thích :
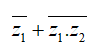= 1 - 2i + 8 - i = 9 - 3i
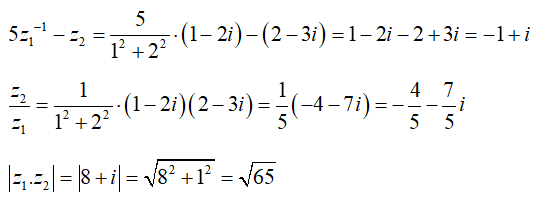
Câu 21:Tính tổng 
Đáp án : A
Giải thích :
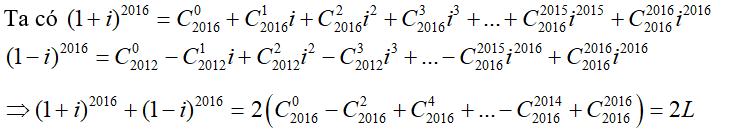
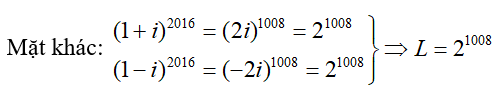
Câu 22:Cho hai số phức z1;z2 khác 0 thỏa mãn z12 - z1z2 + z22 Gọi A,B lần lượt là các điểm biểu diễn cho số phức z1;z2. Khi đó tam giác OAB là:
A. Tam giác đều. B. Tam giác vuông tại O .
C. Tam giác tù. D. Tam giác có một góc bằng 45o
Đáp án : A
Giải thích :
Ta có z13 + z23 = (z1 + z2)(z12 - z1z2 + z22)
suy ra:
z13 = -z23 => |z13| = |z23| => |z1| = |z2| => OA = OB
lại có
(z1 - z2)2 = (z12 - z1z2 + z22 - z1z2 = -z1z2) nên |z1 - z2|2 = |z1|.|z2| => AB2 OA.OB = OA2
Suy ra AB = OA = OB => ΔOAB đều
Câu 23: Cho hai số phức z1 = 1 + i; z2 = -5 + 2i . Tính môđun của số phức z1 + z2.
A. 5. B.-5. C.√7. D.-√7 .
Đáp án : A
Giải thích :
z1 + z2 = (1 + i) + (-5 + 2i) = -4 + 3i
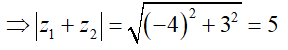
Câu 24: Cho số phức z = (1 - 6i) - (2 - 4i). Phần thực, phần ảo của z lần lượt là
A.-1 ; -2 B. 1 ; 2 C. 2 ; 1. D. –2 ; 1.
Đáp án : A
Giải thích :
Ta có z = (1 - 6i) - (2 - 4i) = 1 - 6i - 2 + 4i = -1 - 2i
Câu 25:Giá trị của i105 + i20 + i23 - i34 là ?
A.2 B.-2 C.4 D.-4
Đáp án : A
Giải thích :
Ta có :
i105 + i23 + i20 - i34 = i4.26 + 1 + i4.5 + 3 + i4.5 - i4.8 + 2 = i - i + 1 + 1 = 2
Câu 26:Với mọi số ảo z, số z2 + |z|2 là:
A. Số thực âm B. Số 0 C. Số thực dương D. Số ảo khác 0
Đáp án : B
Giải thích :
Do z là số ảo nên z có dạng: z = bi.
Ta có: z2 + |z2| = (bi)2 + b2 = -b2 + b2 = 0.
Câu 27: Cho số phức z = 2 – 2i. Tìm khẳng định sai.
A. Phần thực của z là: 2.
B. Phần ảo của z là: -2.
C. Số phức liên hợp của z là z− = -2 + 2i.
D. Môđun của z là
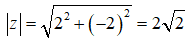
Số phức liên hợp của z là z− = 2 + 2i nên khẳng định C là sai.
Chọn đáp án C.
Câu 28: Cho số phức z = -1 + 3i. Phần thực, phần ảo của z− là
A. -1 và 3 B. -1 và -3 C. 1 và -3 D. -1 và -3i.
Ta có z = -1 + 3i => z− = -1 - 3i
Vậy phần thực và phần ảo của z− là -1 và -3.
Chọn đáp án B.
Câu 29: Môđun của số phức z thỏa mãn z− = 8 - 6i là
A. 2 B. 10 C. 14 D. 2√7
Ta có
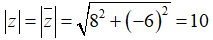
Chọn đáp án B.
Câu 30: Tìm các số thực x, y sao cho (x – 2y) + (x + y + 4).i = (2x + y) + 2yi.
A. x = 3, y = 1 B. x = 3, y = -1
C. x = -3, y = -1 D. x = -3, y = 1
Ta có (x – 2y) + (x + y + 4).i = (2x + y) + 2yi.
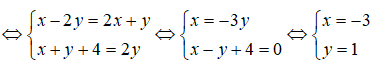
Vậy x = -3, y = 1.
Chọn đáp án D.
Câu 31: Hai số phức z1 = x - 2i, z22 + yi (x, y ∈ R) là liên hợp của nhau khi
A. x = 2, y = -2 B. x = -2, y = -2 C. x = 2, y = 2 D. x = -2, y = 2
Ta có z1− = x + 2i. Do đó, hai số phức đã cho gọi là liên hợp của nhau khi và chỉ khi
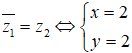
Vậy x= 2, y = 2. Chọn đáp án C.
Câu 32: Tập hợp các điểm biểu diễn số phức z thòa mãn |z| = |1 + i| là
A. Hai điểm B. Hai đường thẳng
C. Đường tròn bán kính R=2 D. Đường tròn bán kính R= √2 .
Ta có |1 + i| = √(1 + 1) = √2. Gọi M là điểm biểu diễn của z ta có |z| = OM.
Do đó: |z| = |1 + i| ⇔ OM = √2
Vậy tập hợp các điểm M biểu diễn số phức z là đường tròn tâm O, bán kính R= √2 .
Chọn đáp án D.
Câu 33: Phần thực của số phức z = -i là
A. -1 B. 1 C. 0 D. -i
Ta có: z = -i = 0 - i nên phần thực của số phức z = -i là 0
Câu 34: Phần ảo của số phức z = -1 là
A. -i B. 1 C. -1 D. 0
Ta có: z= -1 = -1 + 0.i nên phần ảo của số phức z = -1 là 0
Câu 35: Số phức liên hợp của số phức z = 1 + i là
A. 1 – i B. -1 – i C. -1+ i D. 1 + i
Số phức liên hợp của số phức z = 1 + i là z− = 1 - i
Câu 36: Cho z = 2i -1. Phần thực và phần ảo của z− làv
A. 2 và 1 B. -1 và -2 C. 1 và 2i D. -1 và -2i
Câu 37: Môđun của số phức z = -3 + 4i là
A. 5 B. -3 C. 4 D. 7
Ta có: z = -3 + 4i
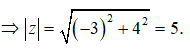
Câu 38: Môđun của số phức z = 2 - √3i là
A. √7 B. 2 + √3 C. 2 - √3 D. 7
Ta có: z = 2 - √3i
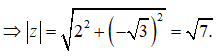
Câu 39: Số phức z = 1 - 2i có điểm biểu diễn là
A. M (1; 2) B. M (1; -2) C. M (-1; 2) D. M (-1; -2)
Số phức z = 1 - 2i có điểm biểu diễn là M(1; -2).
Câu 40: Hai điểm biểu diễn hai số phức liên hợp z = 1 + i và z− = 1 - i đối xứng nhau qua
A. Trục tung B. Trục hoành C. Gốc tọa độ D. Điểm I (1; -1)
Hai điểm biểu diễn của z = 1 + i và z− = 1 - i là M(1; 1) và N(1; -1) đối xứng với nhau qua trục Ox.
Câu 41: Tập hợp các điểm biểu diễn số phức z thỏa mãn |z| = 2 là
A. Hai đường thẳng B. Đường tròn bán kính bằng 2
C. Đường tròn bán kính bằng 4 D. Hình tròn bán kính bằng 2.
Gọi M là diểm biểu diễn của z. Ta có: |z| = 2 ⇔ OM = 2
Vậy quỹ tích của M là đường tròn tâm là gốc tọa độ O và bán kính R = 2.
Câu 42: Gọi A, B là các điểm biểu diễn của các số phức z1 = -1 + 2i, z2 = 2 + 3i . Khi đó, độ dài đoạn thẳng AB là
A. √26 B. √5 + √13 C. √10 D. 10
Ta có: A(-1;2), B(2,3). Do đó:
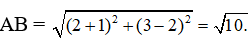
Câu 43. Cho số phức z thỏa mãn |z - 1 + 3i| + |z + 2 - i| = 8. Tìm giá trị lớn nhất, giá trị nhỏ nhất của P = |2z + 1 + 2i|.
A. maxP = 8; minP = √39. B.maxP = 10; minP = √39.
C. maxP = 8; minP = 6. D. max P = 10; minP = 6
Đáp án : A
Giải thích :
Ta có:
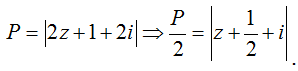
Ta chỉ cần tìm GTLN, GTNN của
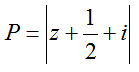
Ta thấy z1 = 1 - 3i; z2 = -2 + i và z0 = 
-i
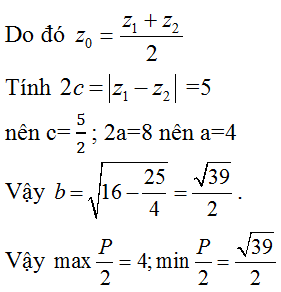
Do đó max P = 8; min P = √39 .
Câu 44. Cho số phức z thỏa mãn:
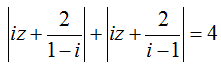
Gọi M vàm n lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của |z| . Tính M.n.
A. 2. B. 1. C. 2√2. D. 2√3.
Đáp án : C
Giải thích :
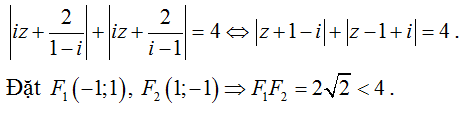
Suy ra quỹ tích điểm biểu diễn số phức z là elíp có tiêu điểm và độ dài trục lớn là 2a = 4 và tiêu cự 2c = 2√2.
Khi đó:
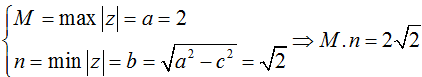
Câu 45. Cho số phức z = a + bi, (a ≥ 0; b ≥ 0; a, b ∈ R). Đặt f(x) = ax2 + bx - 2. Biết:
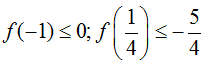
Tính giá trị lớn nhất của |z| .
A. max|z| = 2√5 B. max|z| = 3√2
C. max|z| = 5 D. max|z| = 2√6
Đáp án : A
Giải thích :
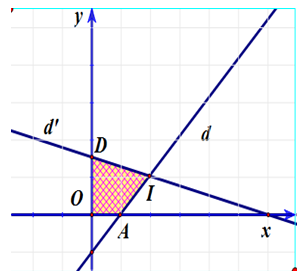
Từ giả thiết ta có:
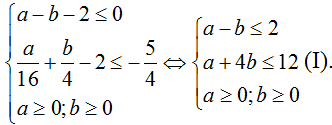
Xét trên hệ tọa độ Oxy các đường thẳng
d: x - y - 2 = 0; d’: x + 4y - 12 = 0 và các trục tọa độ
+ Đường thẳng d ∩ Ox = A(2; 0); d ∩ Oy = (0; -2) = B; d' ∩ Ox = C(12; 0) và hai đường thẳng d ∩ d' = I(4; 2)
+ Miền nghiệm của (I) được biểu diễn trên mặt phẳng tọa độ nằm trong tứ giác OAID kể cả các điểm thuộc trên các cạnh của đa giác.
+ Ta có: |z|2 = a2 + b2 = OM2, |z| lớn nhất khi và chỉ khi OM lớn nhất hay OM2 lớn nhất với M(a; b) là điểm thuộc miền đa giác lồi OAID.
+ Ta có: OA = 2; OI = 2√5; OD = 3. Từ đó suy ra max|z| = 2√5
Dấu bằng diễn ra khi và chỉ khi z = 4 + 2i.
Câu 46. Tập hợp các điểm biểu diễn số phức z thỏa
A. Một parabol. B. Một điểm. C. Một đường thẳng. D. Một đường tròn.
Đáp án : A
Giải thích :
Giả sử z = x + yi, (x, y ∈ R), khi đó ta có: 
= x - yi
Từ đó ta được:
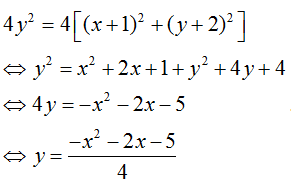
Vậy quỹ tích cần tìm là đường parabol.
Câu 47. Cho hai số phức z1, z2 thỏa mãn |z1| = 2, |z2| = √3 và nếu gọi M, N lần lượt là điểm biểu diễn cho các số phức z1; z2 thì:
A. P = √5. B. P = 4√7. C. P = 3√3. D. P = 5√2
Đáp án : B
Giải thích :
Ta có:
Từ đó ta có: P = |z1 - 2iz2|.|z1 + 2iz2|.
Theo bài gọi điểm biểu diễn cho số phức 2iz là A khi đó N là trung điểm của đoạn OA.
Ta có:
|z1 - 2iz| = MA, theo định lý cô sin cho tam giác OMA ta có:
MA2 = OM2 + OA2 - 2OM.OA.cos30o = 4 + 4.4 - 2.2.2√3.
= 4
Từ đó ta được MA = 2.
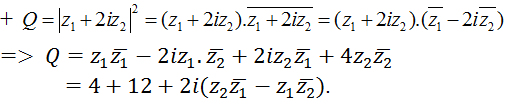
Nếu đặt z1 = a + bi; z2 = x + yi, (a, b, x, y ∈ R), ta có:
Q = 16 + 2i[(x + yi)(a - bi) - (a + bi)(x - yi)] = 16 + 2i(-2bxi + 2ayi) = 16 + 4(bx - ay)
Ta có: iz2 = -y + xi nên ta có:
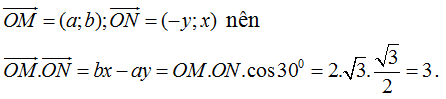
Từ đó ta được Q = 16 + 4.3 = 28, từ đó suy ra |z1 + 2iz2| = 2√7. Từ đó ta được P = 4√7.
Câu 48. Cho số phức z thoả mãn|z| = 1. Gọi M và m là giá trị lớn nhất và nhỏ nhất của biểu thức:
Tính M + m
Đáp án : D
Giải thích :
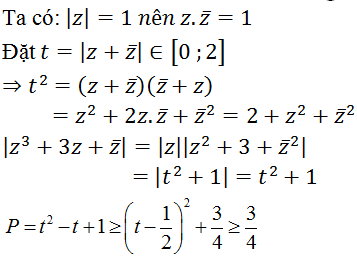
Vậy minP = 
; maxP = 3 khi t = 2
M + n = 
Câu 49 . Cho ba số phức z1; z2; z3 thoả mãn hệ:
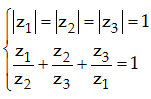
Tính giá trị của biểu thức: T = |az1 + zb2 + cz3|
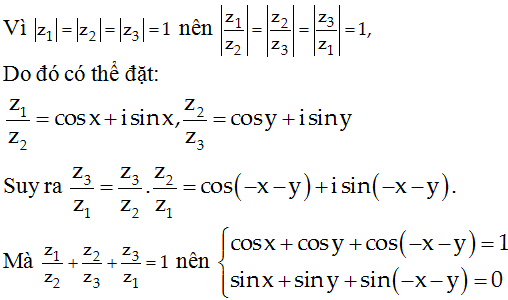
Ta có 0 = sinx + siny + sin(-x - y)
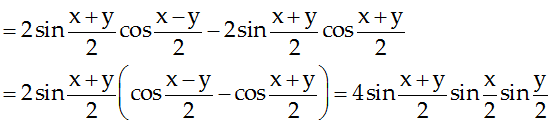
Suy ra hoặc x = k2π hoặc y = k2π hoặc x + y= k2π do đó hai trong ba số z1; z2; z3 bằng nhau.
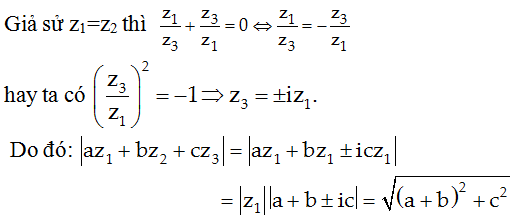
Vậy T nhận một trong ba giá trị sau:
Câu 50. Cho số phức z thoả mãn |z - 3 - 4i| = √5. Gọi M và m là giá trị lớn nhất và giá trị nhỉ nhất của biểu thức P = |z + 2|2 - |z - i|2. Tính module số phức w = M + mi
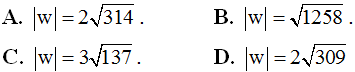
Đáp án : B
Giải thích :
Cách 1:
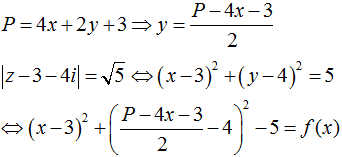
f'(x) = 8(x - 3) - 8(P - 4x - 11) = 0
⇔ x = 0,2P - 1,6
=> y = 0,1P + 1,7
Thay vào f(x) ta được:
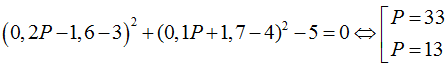
Cách 2:
|z - 3 - 4i| = √5. Nên (x - 3)2 + (y - 4)2 = 5 (C)
Δ 4x + 2y + 3 - P = 0. Tìm P sao cho đường thẳng ∆ và đường tròn (C) có điểm chung
⇔ d(I; Δ) ≤ R ⇔ |23 - P| ≤ 10 ⇔ 13 ≤ P ≤ 33
Vậy Max P = 33; MinP = 12
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.
