Cộng, trừ và nhân số phức(Lý thuyết + 50 bài tập có lời giải)

Đoàn Nguyễn Thành Công Ngày: 01-09-2022 Lớp 12

349

Cộng, trừ và nhân số phức(Lý thuyết + 50 bài tập có lời giải)

A. Tóm tắt lý thuyết

Cho hai số phức z₁ = a + bi và z₂ = c + di thì:

• Phép cộng số phức: z₁ + z₂ = (a + c) + (b + d)i

• Phép trừ số phức: z₁ - z₂ = (a - c) + (b - d)i

- Mọi số phức z = a + bi thì số đối của z là -z = -a - bi: z + (-z) = (-z) + z = 0

• Phép nhân số phức: z₁.z₂ = (ac - bd) + (ad + bc)i

• Phép chia số phức: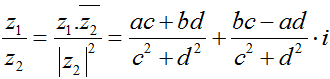 Cộng, trừ và nhân số phức(Lý thuyết + 50 bài tập có lời giải) (ảnh 1) (với z₂ ≠ 0)

- Chú ý :

• Với mọi số thực k và mọi số phức z = a + bi thì:

k(a + b)i = ka + kbi

• Với mọi số phức: 0z = 0

• Phép cộng và phép nhân các số phức có tất cả các tính chất của phép cộng và phép nhân của số thực.

• i^4k = 1; i^{4k + 1} = i; i^{4k + 2} = -1; i^{4k + 3} = -i

B.Bài tập trắc nghiệm

Câu 1: Tổng của hai số phức z₁ = 1 - 2i, z₂ = 2 - 3i là

A. 2 + 5i B. 2 – 5i C. 1 + 5i D. 1 – 5i.

Tổng của hai số phức z₁ = 1 - 2i, z₂ = 1 - 3i là z = (1 + 1) + (-2 - 3)i = 2 - 5i

Câu 2: Cho hai số phức z₁ = 2 + 3i, z₂ = 2 - 4i . Hiệu z₁ - z₂ bằng

A. 2 + 7i B. 2 – i C. 7i D. – 7i.

Hiệu của hai số phức z₁ = 2 + 3i, z₂ = 2 - 4i là z = (2 - 2) + (3 -(-4))i = 7i

Câu 3: Tích của hai số phức z₁ = 3 + 2i, z₂ = 2 - 3i là

A. 6 – 6i B. 12 C. – 5i D. 12 – 5i.

Tích của hai số phức z₁ = 3 + 2i, z₂ = 2 - 3i là z = (3 + 2i)(2 - 3i) = 6 - 9i + 4i - 6i² = 6 - 5i + 6 = 12 - 5i

Câu 4: Số phức z = (1 + i)² bằng

A. 2i B. 1 + 3i C. – 2i D. 0.

Ta có: z = (1 + i)² = 1 + 2i + i² = 1 + 2i - 1 = 2i

Câu 5: Số phức z = (1 - i)³ bằng

A. 1 + i B. – 2 – 2i C. – 2 + 2i D. 4 + 4i

Ta có: z = (1 - i)³ = 1 - 3i + 3i² - i³ = 1 - 3i - 3 + i = -2 - 2i

Câu 6: Môđun của tổng hai số phức z₁ = 3 - 4i và z₂ = 4 + 3i là

A. 5√2 B. 8 C. 10 D. 50.

Ta có: z₁ + z₂ = (3 + 4) + (-4 + 3)i = 7 - i

Câu 7: Cho hai số phức z₁ = 2 + 3i, z₂ = 1 - 2i . Tìm khẳng định sai

A. z₁ + z₂ = 3 + i B. z₁ - z₂ = 1 + 5i

C. z₁.z₂ = 8 - i D.z₁. z₂ = 8 + i

Tổng của z₁ và z₂ là z₁ + z₂ = (2 + 1) + (3 - 2)i = 3 + i

Hiệu của z₁ và z₂ là z₁ - z₂ = (2 - 1) + (3 + 2)i = 1 + 5i

Tích của z₁ và z₂ là z₁. z₂ = (2 + 3i)(1 - 2i) = 2 - 4i + 3i - 6i² = 2 - i + 6 = 8 - i

Vậy chọn đáp án D.

Câu 8: Cho hai số phức z₁= - 3 + 4i, z₂ = 4 - 3i . Môđun của số phức z = z₁ + z₂ + z₁. z₂ là

A. 27 B. √27 C. √677 D. 677.

Ta có

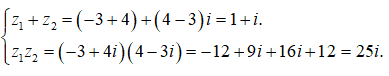
Cộng, trừ và nhân số phức(Lý thuyết + 50 bài tập có lời giải) (ảnh 2)

Do đó z = z₁ + z₂ + z₁. z₂ = 1 + i + 25i = 1 + 26i

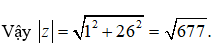
Cộng, trừ và nhân số phức(Lý thuyết + 50 bài tập có lời giải) (ảnh 3)

Chọn đáp án C.

Câu 9: Phần thực và phần ảo của số phức z = (3 + 4i)(4 - 3i) + (2 - i)(3 + 2i) là

A. 32 và 8i B.32 và 8 C. 18 và -14 D. 32 và -8

Ta có

z = (12 - 9i + 16i - 12i²) + (6 + 4i - 3i - 2i²) = (12 + 7i + 12) + (6 + i + 2) = 32 + 8i

Chọn đáp án B.

Câu 10: Cho các số phức z₁ = -1 + i, z₂ = 1 - 2i, z₃ = 1 + 2i . Giá trị của biểu thức T = |z₁z₂ + z₂z₃ + z₃z₁| là

B. 1 B. √13 C. 5 D. 13.

Ta có:

z₂z₃ = (1 - 2i)(1 + 2i) = 1 - 4i² = 5

z₁z₂ + z₁z₃ = z₁(z₂ + z₃) = (-1 + i)(1 - 2i + 1 + 2i) = -2 + 2i

Suy ra

Chọn đáp án B.

Câu 11: Tổng của hai số phức z₁ = 1 - 2i, z₂ = 2 - 3i là

A. 2 + 5i B. 2 – 5i C. 1 + 5i D. 1 – 5i.

Tổng của hai số phức z₁ = 1 - 2i, z₂ = 1 - 3i là z = (1 + 1) + (-2 - 3)i = 2 - 5i.

Câu 12: Cho hai số phức z₁ = 2 + 3i, z₂ = 2 - 4i . Hiệu z₁ - z₂ bằng

A. 2 + 7i B. 2 – i C. 7i D. – 7i.

Hiệu của hai số phức z₁ = 2 + 3i, z₂ = 2 - 4i là z = (2 - 2) + (3 -(-4))i = 7i

Câu 13: Tích của hai số phức z₁ = 3 + 2i, z₂ = 2 - 3i là

A. 6 – 6i B. 12 C. – 5i D. 12 – 5i.

Tích của hai số phức z₁ = 3 + 2i, z₂ = 2 - 3i là:

z = (3 + 2i)(2 - 3i) = 6 - 9i + 4i - 6i² = 6 - 5i + 6 = 12 - 5i

Câu 14: Số phức z = (1 + i)² bằng

A. 2i B. 1 + 3i C. – 2i D. 0.

Ta có: z = (1 + i)² = 1 + 2i + i² = 1 + 2i - 1 = 2i

Câu 15: Số phức z = (1 - i)³ bằng

A. 1 + i B. – 2 – 2i C. – 2 + 2i D. 4 + 4i

Ta có:

z = (1 - i)³ = 1 - 3i + 3i² - i³

= 1 - 3i - 3.(-1) - i²i = 1 - 3i - 3 + i = -2 - 2i

Câu 16: Môđun của tổng hai số phức z₁ = 3 - 4i và z₂ = 4 + 3i là

A. 5√2 B. 8 C. 10 D. 50.

Ta có: z₁ + z₂ = (3 + 4) + (-4 + 3)i = 7 - i

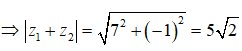
Cộng, trừ và nhân số phức(Lý thuyết + 50 bài tập có lời giải) (ảnh 5)

Câu 17: Cho z = -1 + 3i . Số phức w = iz− + 2z bằng

A. 1 + 5i B. 1 + 7i C. – 1 + 5i D. – 1 + 7i

Ta có: z = -1 + 3i => z− = -1 - 3i => iz− = - i - 3i² = 3 - i

Suy ra: w = 2z + z− = 3 - i + 2(-1 + 3i) = 1 + 5i

Câu 18: Cho z = 1 + 2i . Phần thực và phần ảo của số phức w = 2z + z− là

A. 3 và 2 B. 3 và 2i C. 1 và 6 D. 1 và 6i

Ta có: w = 2z + z− = 2(1 + 2i) + (1 - 2i) = 3 + 2i

Vậy phần thực của w là 3, phần ảo của w là 2

Câu 19: Cho số phức z thỏa mãn (1 + 2i)z + iz− = 2i . Khi đó tích z.iz− bằng

A. – 2 B. 2 C. – 2i D. 2i.

Đặt z = a + bi(a, b ∈ R).

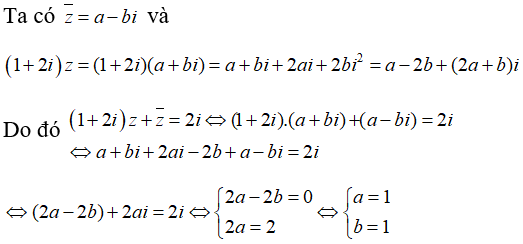
Cộng, trừ và nhân số phức(Lý thuyết + 50 bài tập có lời giải) (ảnh 6)

Suy ra z = 1 + i. Vậy z.z− = |z−|² = 1² + 1² = 2

Câu 20: Môđun của số phức z thỏa mãn 2z + 3(1 - i)iz− = 1 - 9i là

A. 5 B. 13 C. √5 D. √13

Đặt z = a + bi (a, b ∈ R). Ta có: z− = a - bi và (1 - i)z− = (1 - i)(a - bi) = a - bi - ai + bi² = a - b - (a + b)i Do đó 2z + 3(1 - i)z− = 1 - 9i <=> 2(a + bi) + 3[a - b - (a + b)i] = 1 - 9i

<=> (5a - 3b) - (3a + b)i = 1 - 9i

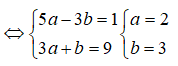
Cộng, trừ và nhân số phức(Lý thuyết + 50 bài tập có lời giải) (ảnh 7)

Câu 21: Cho hai số phức z₁, z₂ thỏa mãn |z₁| = |z₂| = |z₁ + z₂| = 1 . Khi đó |z₁ - z₂| bằng

A. 0 B. 1 C. 2 D. √3

Ta có: |z₁| = |z₂| = 1 => z₁z₁− = z₂z₂− = 1

|z₁| + |z₂| = 1

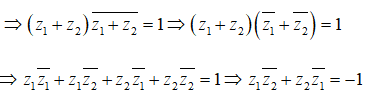
Cộng, trừ và nhân số phức(Lý thuyết + 50 bài tập có lời giải) (ảnh 8)

Do đó

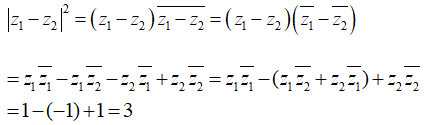
Cộng, trừ và nhân số phức(Lý thuyết + 50 bài tập có lời giải) (ảnh 9)

Vậy |z₁| - |z₂| = √3

Câu 22: Tập hợp các điểm biểu diễn số phức z thỏa mãn |z + 1 - 2i| = 2 là

A. Đường tròn tâm I(1; -2) bán kính R = 2

B. Đường tròn tâm I(1; -2) bán kính R = 4

C. Đường tròn tâm I(-1; 2) bán kính R = 2

D. Đường tròn tâm I(-1; 2) bán kính R = 4

Đặt z = a + bi(a, b ∈ R). Ta có: z + 1 - 2i = (a + 1) + (b - 2)i. Do đó:

|z + 1 - 2i| = 2 <=> (a + 1)² + (b - 2)² = 4

Vậy tập hợp điểm M biểu diễn số phức z là đường tròn tâm I(-1 ;2), bán kính R = 2

Câu 23: Cho hai số phức z₁ = 2 + 3i, z₂ = 1 - 2i . Tìm khẳng định sai

A. z₁ + z₂ = 3 + i

B. z₁ - z₂ = 1 + 5i

C. z₁.z₂ = 8 - i

D.z₁. z₂ = 8 + i

Tổng của z₁ và z₂ là z₁ + z₂ = (2 + 1) + (3 - 2)i = 3 + i

Hiệu của z₁ và z₂ là z₁ - z₂ = (2 - 1) + (3 + 2)i = 1 + 5i

Tích của z₁ và z₂ là z₁. z₂ = (2 + 3i)(1 - 2i) = 2 - 4i + 3i - 6i² = 2 - i + 6 = 8 - i

Chọn đáp án D

Câu 24: Phần thực và phần ảo của số phức z = (3 + 4i)(4 - 3i) + (2 - i)(3 + 2i) là

A. 32 và 8i

B.32 và 8

C. 18 và -14

D. 32 và -8

Ta có

z = (12 - 9i + 16i - 12i²) + (6 + 4i - 3i - 2i²) = (12 + 7i + 12) + (6 + i + 2) = 32 + 8i

Chọn đáp án B

Câu 25: Cho các số phức z₁ = -1 + i, z₂ = 1 - 2i, z₃ = 1 + 2i . Giá trị của biểu thức T = |z₁z₂ + z₂z₃ + z₃z₁| là

B. 1

B. √13

C. 5

D. 13

Ta có:

z₂z₃ = (1 - 2i)(1 + 2i) = 1 - 4i² = 5

z₁z₂ + z₁z₃ = z₁(z₂ + z₃) = (-1 + i)(1 - 2i + 1 + 2i) = -2 + 2i

Suy ra

Chọn đáp án B

Câu 26: Tổng của hai số phức z₁ = 1 - 2i, z₂ = 2 - 3i là

A. 2 + 5i

B. 2 – 5i

C. 1 + 5i

D. 1 – 5i

Tổng của hai số phức z₁ = 1 - 2i, z₂ = 1 - 3i là z = (1 + 1) + (-2 - 3)i = 2 - 5i.

Câu 27: Cho hai số phức z₁ = 2 + 3i, z₂ = 2 - 4i . Hiệu z₁ - z₂ bằng

A. 2 + 7i

B. 2 – i

C. 7i

D. – 7i

Hiệu của hai số phức z₁ = 2 + 3i, z₂ = 2 - 4i là z = (2 - 2) + (3 -(-4))i = 7i

Chọn đáp án C

Câu 28: Tích của hai số phức z₁ = 3 + 2i, z₂ = 2 - 3i là

A. 6 – 6i

B. 12

C. – 5i

D. 12 – 5i

Tích của hai số phức z₁ = 3 + 2i, z₂ = 2 - 3i là:

z = (3 + 2i)(2 - 3i) = 6 - 9i + 4i - 6i² = 6 - 5i + 6 = 12 - 5i

Chọn đáp án D

Câu 29: Tìm số thực x; y để hai số phức $z_{1} = 9 y^{2} - 4 - 10 x i^{5}$ và $z_{2} = 82 + 20 i^{11}$ là liên hợp của nhau?

A. $x = - 2; y = 2.$
B. $x = 2; y = \pm 2 .$
C. $x = 2; y = 2.$
D. $x = - 2; y = \pm 2 .$

Câu 30: Tổng của hai số phức $z$ ₁ = $1 - 2 i$ , $z$ ₂ = 2 - $3 i$ là

A. $2 + 5 i$
B. $2 - 5 i$
C. $1 + 5 i$
D. $1 - 5 i .$

Câu 31: Có bao nhiêu số phức z thỏa mãn: $| z |^{2} + | \bar{z} |^{2} = 26$ và $z + \bar{z}$ = 6

A. 2.
B. 3.
C. 2.
D. 1

Câu 32: Cho hai số phức $z_{1} = 2 + 3 i, z_{2} = 2 - 4 i$ . Hiệu $z_{1} - z_{2}$ bằng

A. $2 + 7 i$
B. $2 - i$
C. $7 i$
D. $- 7 i .$

Câu 33: Cho số phức $z = a + b i$ thỏa mãn

$(z + 1 + i) (\bar{z} - i) + 3 i = 9$ và $| \bar{z} |$ > 2

Tính $P = a + b i$

A.-3
B.-1
C.1
D.2

Câu 34: Tích của hai số phức $z_{1} = 3 + 2 i, z_{2} = 2 - 3 i$ là

A. $6 - 6 i$
B. $12$
C. $- 5 i$
D. $12 - 5 i .$

Câu 35: Cho số phức $z_{1} = 1 + 2 i$ và $z_{2} = - 2 - 2 i$ . Tìm modun của số phức $z_{1} - z_{2}$ ?

A. $| z_{1} - z_{2} |$ = 2 $\sqrt{2}$
B. $| z_{1} - z_{2} |$ = 1
C. $| z_{1} - z_{2} |$ = $\sqrt{17}$
D. $| z_{1} - z_{2} |$ = 5

Câu 36: Số phức z $= (1 + i)^{2}$ bằng

A. $2 i$
B. $1 + 3 i$
C. $- 2 i$
D. 0.

Câu 37: Số phức $z = (1 - i)^{3}$ bằng

A. $1 + i$
B. $- 2 - 2 i$
C. $- 2 + 2 i$
D. $4 + 4 i$

Câu 38: Cho số phức $z$ thỏa mãn $| z - 4 | + | z + 4 |$ = 10. Giá trị lớn nhất và nhỏ nhẩ của $| z |$ lần lượt là:

A. 10 và 4
B. 5 và 4
C. 4 và 3
D. 5 và 3

Câu 39: Môđun của tổng hai số phức $z - 1 = 3 - 4 i$ và $z_{2} = 4 + 3 i$ là

A. 5 $\sqrt{2}$
B. 8
C. 10
D. 50.

Câu 40: Cho số phức $z$ thỏa mãn $(1 - i) z + 2 i \bar{z} = 5 + 3 i$ . Modun của $z$ là:

A. $\sqrt{3}$
B. $\sqrt{5}$
C. 5
D. 3

Câu 41: Cho $z = - 1 + 3 i$ . Số phức $w = i \bar{z} + 2 z$ bằng

A. $1 + 5 i$
B. $1 + 7 i$
C. $- 1 + 5 i$
D. $- 1 + 7 i$

Câu 42: Cho số phức $z$ thỏa mãn điều kiện $2 z - i \bar{z} = 2 + 5 i$ . Số phức $z$ cần tìm là:

A. $z = 3 + 4 i$
B. $z = 3 - 4 i$
C. $z = 4 + 3 i$
D. $z = 4 - 3 i$

Câu 43: Cho $z = 1 + 2 i$ . Phần thực và phần ảo của số phức $w = 2 z + \bar{z}$ là

A. 3 và 2
B. $3 v a ̀ 2 i$
C. 1 và 6
D. $1 v a ̀ 6 i$

Câu 44: Cho số phức z thỏa mãn $(1 + 2 i) z + i \bar{z} = 2 i$ . Khi đó tích $z . i \bar{z}$ bằng

A. – 2
B. 2
C. – 2 $i$
D. 2 $i$ .

Câu 45: Môđun của số phức z thỏa mãn $2 z + 3 (1 - i) i \bar{z} = 1 - 9 i$ là

A. 5
B. 13
C. $\sqrt{5}$
D. $\sqrt{13}$

Câu 46: Cho hai số phức $z_{1}, z_{2}$ thỏa mãn $| z_{1} | = | z_{2} | = | z_{1} + z_{2} | = 1$ . Khi đó $| z_{1} - z_{2} |$ bằng

A. 0
B. 1
C. 2
D. $\sqrt{3}$

Câu 47: Tập hợp các điểm biểu diễn số phức $z$ thỏa mãn $| z + 1 - 2 i |$ = 2 là

A. Đường tròn tâm $I (1; - 2)$ bán kính $R = 2$
B. Đường tròn tâm $I (1; - 2)$ bán kính $R = 4$
C. Đường tròn tâm $I (- 1; 2)$ bán kính $R = 2$
D. Đường tròn tâm $I (- 1; 2)$ bán kính $R = 4$

Câu 48: Cho $z_{1}, z_{2}, z_{3}$ là các số phức thỏa mãn:

$z_{1} + z_{2} + z_{3} = 0$ và $| z_{1} | = | z_{2} | = | z_{3} |$

Khẳng định nào dưới đây sai?

A. $| z_{1}^{3} + z_{2}^{3} + z_{3}^{3} | = | z_{1} |^{3} + | z_{2} |^{3} + | z_{3} |^{3}$
B. $| z_{1}^{3} + z_{2}^{3} + z_{3}^{3} | \leq | z_{1} |^{3} + | z_{2} |^{3} + | z_{3} |^{3}$
C. $| z_{1}^{3} + z_{2}^{3} + z_{3}^{3} | \geq | 3 + | z_{2} |^{3} + | z_{3} |^{3}$
D. $| z_{1}^{3} + z_{2}^{3} + z_{3}^{3} | \neq | z_{1} |^{3} + | z_{2} |^{3} + | z_{3} |^{3}$