Toptailieu.vn xin giới thiệu 50 bài tập trắc nghiệm Ôn tập chương 4 (có đáp án) chọn lọc, hay nhất giúp học sinh lớp 12 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán.
Mời các bạn đón xem:
Ôn tập chương 4
Câu 1: Cho hai số phức z1 = 1 + 2i, z2 = 2 - 3i . Phần thực và phần ảo của số phức w = 3z1 - 2z2 là
A. 1 và 12
B. -1 và 12
C. –1 và 12i
D. 1 và 12i.
Lời giải:
Ta có: w = 3z1 - 2z2 = 3(1 + 2i) - 2(2 - 3i) = -1 + 2i.
Vậy phần thực và phần ảo của w là -1 và 12
Đáp án cần chọn là:B
Câu 2: Phần thực và phần ảo của số phức z = (1 + √3i)2 là
A. 1 và 3
B. 1 và -3
C. -2 và 2√3
D. 2 và -2√3 .
Lời giải:
Ta có: z = 1 + 2√3 + 3i2 = -2 + 2√3i
Vậy phần thực và phần ảo của z là -2 và 2√3
Đáp án cần chọn là:C
Câu 3: Phần ảo của số phức z = (1 + √i)3 là
A. 3√3
B. -3√3
C. – 8i
D. –8.
Lời giải:
Ta có: z = i(1 + √3i)3 = i(1 + 3√3i - 9 - 3√3i) = -8i .
Vậy phần ảo của z là -8
Đáp án cần chọn là:D
Câu 4: Thực hiện phép tính:
ta có:
A. T = 3 + 4i
B. T = -3 + 4i
C. T = 3 – 4i
D. T = -3 – 4i.
Lời giải:
Ta có:
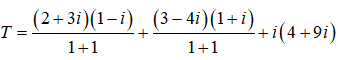
=> T = -3 + 4i
Đáp án cần chọn là:B
Câu 5: Môđun của số phức z thỏa mãn điều kiện z + (2 - i)z− = 13 - 3i là
A. 3
B. 5
C. 17
D. √17
Lời giải:
Môđun của số phức z thỏa mãn điều kiện z + (2 - i)z− = 13 - 3i là:
Đặt z = a + bi(a, b ∈ R). Ta có: z− = a - bi và (2 - i)z− = (2 - i)(a - bi) = 2a - 2bi - ai - b = 2a - b - (2b + a)i
Do đó : z = (2 - i)z− = 13 - 3i ⇔ a + bi + 2a - b - (2b + a)i = 13 - 3i
Đáp án cần chọn là:D
Câu 6: Phần thực và phần ảo của số phức z thỏa mãn (1 - i)z - 1 + 5i = 0 là
A. 3 và –2
B. 3 và 2
C. 3 và – 2i
D. 3 và 2i.
Lời giải:
Ta có: (1 - i)z - 1 + 5i = 0 ⇔ (1 - i)z = 1 - 5i
Vậy phần thực và phần ảo của z là 3 và -2
Đáp án cần chọn là:A
Câu 7: Môđun của số phức z thỏa mãn điều kiện (3z - z−)(1 + i) - 5z = 8i - 1 là
B. 1
B. 5
C. √13
D. 13.
Lời giải:
Đặt z = a + bi(a, b ∈ R).
Ta có: z− = a - bi và 3z - z− = 3(a + bi) - (a - bi) = 2a + 4bi,
Do đó: (3z - z−)(1 + i) = 2a - 4b + (2a + 4b)i - 5(a + bi) = 8i - 1
Theo giả thiết: (2a - 4b) + (2a + 4b)i - 5(a + bi) = 8i - 1
⇔ -3a - 4b + (2a - b)i = -1 + 8i
Đáp án cần chọn là:C
Câu 8: Cho số phức z thỏa mãn: i.z− + z = 2 + 2i và z.z− = 2. Khi đó z2 bằng:
A. 2
B. 4
C. – 2i
D. 2i.
Lời giải:
Đặt z = a + bi(a, b ∈ R). Ta có: z− = a - bi và z.z− = a2 + b2 = 2(1)
Ta có: i.z− + z = 2 + 2i ⇔ i(a - bi) + a + bi = 2 + 2i
⇔ a + b + (a + b)i = 2 + 2i ⇔ a + b = 2 (2)
Từ (1) và (2) suy ra a = b = 1. Suy ra z=1+i
Vậy z2 = (1 + i)2 = 1 + 2i - 1 = 2i
Đáp án cần chọn là:D
Câu 9: Cho số phức z thỏa mãn (1 + i)(z - i) + 2z = 2i. Môđun của số phức:
A. 2
B. 4
C. √10
D. 10
Lời giải:
Đặt z = a + bi(a, b ∈ R). Ta có :
(1 + i)(z - i) = (1 + i)[a + (b - 1)i] = a - b + 1 + (a + b - 1)i
Từ giả thiết ta có: (1 + i)(z - 1) + 2z = 2i
⇔ a - b + 1 + (a + b - 1)i + 2(a + bi) = 2i ⇔ (3a - b + 1) + (a + 3b - 1)i = 2i
Suy ra z = 1 và
Đáp án cần chọn là:C
Câu 10: Cho số phức z thỏa mãn
Khi đó môđun của số phức w = 1 + z + z2 là
A. 5
B. √13
C. 13
D. √5
Lời giải:
Đặt z = a + bi(a, b ∈ R). Ta có
⇔ 5a - 5(b - 1)i = (2 - i)(a + 1 + bi)
⇔ 3a - b - 2 + (a - 7b + 6)i = 0
Suy ra z = 1 + i và w = 1 + (1 + i) + (1 + i)2 = 2 + 3i.
Vậy: |w| = √(4 + 9) = √13
Đáp án cần chọn là:B
Câu 11: Phương trình z4 - 2z2 - 3 = 0 có 4 nghiệm phức z1, z2, z3, z4. Giá trị biểu thức T = |z1|2 + |z2|2 + |z3|2 + |z4|2 bằng
A. 4
B. 8
C. 2√3
D. 2 + 2√3
Lời giải:
Phương trình tương đương với: z2 = -1 = i2 hoặc z2 = 3. Các nghiệm của phương trình là: z1 = i, z2 = -i, z3 = √3, z4 = -√-3.
Vậy T = 1 + 1 + 3 + 3 = 8
Đáp án cần chọn là:B
Câu 12: Tập hợp các điểm biểu diễn số phức z thỏa mãn |z - 2i| = 4 là
A. Đường tròn tâm I(1; -2) bán kính R = 4
B. Đường tròn tâm I(1; 2) bán kính R = 4
C. Đường tròn tâm I(0; 2) bán kính R = 4
D. Đường tròn tâm I(0; -2) bán kính R = 4
Lời giải:
Đặt z = a + bi(a, b ∈ R). Ta có:
|z - 2i| = 4 ⇔ |a + (b - 2)i| = 4
Vậy tập các điểm biểu diễn số phức z là đường tròn tâm I(0 ;2), bán kính R = 4
Đáp án cần chọn là:C
Câu 13: Tập hợp các điểm biểu diễn số phức z thỏa mãn |z− + 3 - 2i| = 4 là
A. Đường tròn tâm I(3; 2) bán kính R = 4
B. Đường tròn tâm I(3; -2) bán kính R = 4
C. Đường tròn tâm I(-3; 2) bán kính R = 4
D. Đường tròn tâm I(-3; -2) bán kính R = 4
Lời giải:
Đặt z = a + bi(a, b ∈ R). Ta có: |z− + 3 - 2i| = 4 ⇔ |a - bi + 3 - 2i| = 4
⇔ |(a + 3) - (b + 2)i| = 4
Vậy tập các điểm biểu diễn số phức z là đường tròn tâm I(-3 ;-2), bán kính R = 4
Đáp án cần chọn là:D
Câu 14: Cho số phức z thỏa mãn điều kiện |z - 3 + 4i| ≤ 2. Trong mặt phẳng Oxy tập hợp điểm biểu diễn số phức w = 2z + 1 - i là hình tròn có diện tích:
A. S = 9π
B. S = 12π.
C. S = 16π.
D.S = 25π.
Lời giải:
Ta có:
<=> |w - 1 + i - 6 + 8i| ≤ 4 <=> |w - 7 + 9i| ≤ 4 (1)
Giả sử w = x + yi, khi đó (1) <=> (x - 7)2 + (y + 9)2 ≤ 16
Suy ra tập hợp điểm biểu diễn số phức w là hình tròn tâm I(7; -9), bán kính r = 4
Vậy diện tích cần tìm là S = π.42 = 16π
Đáp án cần chọn là:C
Câu 15: Cho số phức z thỏa mãn |z| = 1. Tìm giá trị lớn nhất của biểu thức
A.5
B.4
C.6
D.8
Lời giải:
Ta có:
Khi z = i thì A = 6
Đáp án cần chọn là:C
Câu 16. Cho số phức z thỏa mãn |z| = 1. Tìm giá trị lớn nhất max M và giá trị nhỏ nhất min M của biểu thức M = |z2 + z + 1| + |z3 + 1|
A. max M = 5; min M = 1
B. max M = 5; min M = 2
C. max M = 4; min M = 1
D.max M = 4; min M = 2
Lời giải:
Ta có: M ≤ |z|2 + |z| + 1 + |z|3 + 1 = 5 ,
khi z = 1 thì M = 5 nên max M = 5
Mặt khác:
khi z = -1 thì M = 1 nên min M = 1
Đáp án cần chọn là:A
Câu 17. Cho z1; z2 là hai số phức liên hợp của nhau và thỏa mãn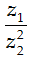 
∈ R và |z1 - z2| = 2√3. Tính môđun của số phức z1.
A. |z1| = √5
B. |z1| = 3
C. |z1| = 2
D. |z1| = 
Lời giải:
Gọi z1 = a + bi; z2 = a - bi.
Không mất tính tổng quát ta coi b ≥ 0
Do |z1 - z2| = 2√3 => |2bi| = 2√3 => b = √3
Do z1; z2 là hai số phức liên hợp của nhau nên z1; z2 ∈ R, mà:
Ta có:
(z1)3 = (a + bi)3 = (a3 - 3ab2) + (3a2b - b3)i ∈ R
Đáp án cần chọn là:C
Câu 18. Biết số phức z thỏa mãn đồng thời hai điều kiện |z - 3 - 4i| = √5 và biểu thức M = |z + 2|2 - |z - i|2 đạt giá trị lớn nhất. Tính môđun của số phức z + i.
A. |z + i| = 2√41
B. |z + i| = 3√5
C. |z + i| = 5√2
D. |z + i| = √41
Lời giải:
Gọi z = x + yi.
Ta có: |z - 3 - 4i| = √5 <=> (C): (x - 3)2 + (y - 4)2 = 5, tâm I(3; 4) và R = √5
Mặt khác:
M = |z + 2|2 - |z - i|2 = (x + 2)2 + y2 - [(x2) + (y - 1)2] = 4x + 2y + 3
<=> d: 4x + 4y + 3 - M = 0
Do số phức z thỏa mãn đồng thời hai điều kiện nên d và (C) có điểm chung
Đáp án cần chọn là:D
Câu 19. Cho số phức z thỏa mãn điều kiện: |z - 1 + 2i| = √5 và w = z + 1 + i có môđun lớn nhất. Số phức z có môđun bằng:
A. 2√5
B. 3√2
C. √6
D. 5√2
Lời giải:
Gọi z = x + y; khi đó: z - 1 + 2i = (x - 1) + (y + 2)i
Ta có:
Suy ra tập hợp điểm M(x; y) biểu diễn số phức z thuộc đường tròn (C) tâm I(1; -2) bán kính R = √5 như hình vẽ:
Dễ thấy O ∈ (C), N(-; -1) ∈ (C),
Theo đề ta có: M(x; y) ∈ (C) là điểm biểu diễn cho số phức z thỏa mãn: w = z + 1 + i = x + yi + 1 + i = (x + 1) + (y + 1)i
Suy ra |z + 1 + i|đạt giá trị lớn nhất khi MN lớn nhất
Mà M, N ∈ (C) nên MN lớn nhất khi MN là đường kính đường tròn (C)
Khi và chỉ khi I là trung điểm MN => M(3; 3) => z = 3 - 3i
Đáp án cần chọn là:B
Câu 20. Gọi A, B, C lần lượt là điểm biểu diễn các số phức
Khi đó, mệnh đề nào dưới đây là đúng.
A. A; B; Cthẳng hàng.
B. Tam giác ABC là tam giác tù.
C. ΔABC là tam giác đều.
D. Tam giác ABC là tam giác vuông cân.
Lời giải:
Ta có z1 = 2 - i; z2 = 3 + i; z3 = 2i.
Từ trên ta được A( 2; -1); B(3; 1); C(0; 2).
Ta được:
- Do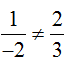 
nên ba điểm A; B; C không thẳng hàng từ đó ta được tam giác ABC.
- Dễ thấy tam giác ABC không phải là tam giác đều và cũng không phải tam giác vuông.
Vậy tam giác ABC là tam giác tù.
Đáp án cần chọn là:B
Câu 21. Cho 3 số phức z1; z2; z3 phân biệt thỏa mãn |z1| = |z2| = |z3| = 3 và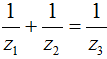 
Biết rằng các điểm biểu diễn cho các số phức z1; z2; z3 lần lượt là A; B; C. Tính số đo góc ∠ACB
A. 60o
B. 90o
C. 150o
D. 120o
Lời giải:
Giả sử zk = xk + yk, khi đó điểm A(x1; y1); B( x2; y2); C(x3; y3) lần lượt là điểm biểu diễn cho các số phức z1; z2; z3 trên mặt phẳng tọa độ Oxy.
+ Từ giả thiết |z1| = |z2| = |z3| = 3 => OA = OB = OC = 3nên A; B; C đều thuộc đường tròn tâm O, bán kính R = 3.
(vì |z1| = |z2| = |z3| = 3 ) hay x1 - y1.i + x2 - y2.i = x3 - y3i.
+ Vì OA = OB = 3 và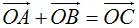 
nên OACB là hình thoi với một đường chéo OC = 3.
+ Từ trên suy ra tam giác OAC; OBC đều cạnh bằng 3 nên ∠ACB = 120o
Đáp án cần chọn là:D
Câu 22. Cho các số phức a; b; c; z thỏa mãn az2 + bz + c = 0 và |a| = |b| = |c| > 0 . Kí hiệu M = max|z|, m = min|z|. Tính mô đun của số phức w = M - mi.
A. |w| = √3
B. |w| = 1
C. |w| = 2√3
D. |w| = 2
Lời giải:
Ta thấy phương trình az2 + bz + c = 0 trên tập số phức luôn có hai nghiệm phân biệt hoặc trùng nhau z1; z2.
Theo định lý vi – ét ta có:
Đặt |z1| = x > 0; x ∈ R , khi đó ta có:
Từ bất đẳng thức |z1| + |z2| ≥ |z1 + z2| nên ba số |z1|, |z2|, |z1 + z2| là 3 cạnh của một tam giác (có thể suy biến thành đoạn thẳng).
Áp dụng bất đẳng thức tam giác ngược ta được:
Đáp án cần chọn là:A
Câu 23. Cho số phức z thỏa mãn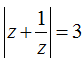 
. Tổng giá trị lớn nhất, nhỏ nhất của |z| là:
A. 3
B. √5
C. √13
D. 5
Lời giải:
Với giả thiết ta có:
Từ đó ta được:
Từ đó bằng cách thay a cụ thể ta được đáp án C.
Đáp án cần chọn là:C
Câu 24. Cho số phức z thỏa mãn |z| = 1 Tìm tổng giá trị lớn nhất, nhỏ nhất của biểu thức P với P = |1 + z22| - |1 + z| ?
A. 2 + √2
B. 1 + 2√2
C. -1 + 2√2
D. 2 - √2
Lời giải:
Ta có:
nên ta có maxP = P(1) = 0; minP = P(0) = -√2.
Hàm số nghịch biến trên .
Từ đó ta được max P = P(-1) = 2; minP = P(0) = -√2.
+ Từ trên ta được:
Đáp án cần chọn là:A
Câu 25. Cho hai số phức z1; z2 thỏa mãn |z1|z1 = 4|z2|z2 và nếu gọi M, N là điểm biểu diễn z1;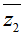 
trong mặt phẳng tọa độ thì tam giác giác MON có diện tích là 8. Tìm giá trị nhỏ nhất của |z1 + z2|
A. 3√3
B.8
C. 6√2
D.5
Lời giải:
Giải theo tự luận
+ Từ giả thiết |z1|z1 = 4|z2|z2, suy ra |z1| = 2|z2| và ta được z1 = 2z2.
+ Giả sử z1 = x + yi; z2 = a + bi. Ta được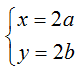 
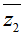
và M(x; y); N(a; -b); N’(a; b) lần lượt là các điểm biểu diễn cho các số phức z1, và z2.
Ta có:
Từ diện tích của tam giác OMN bằng 8 nên |bx + ay| = 16 hay |ab| = 4 (1).
Ta có:
Dấu bằng diễn ra khi và chỉ khi :
Đáp án cần chọn là:C
Câu 26. Cho số phức z thỏa mãn |z - 1 + 3i| + |z + 2 - i| = 8. Tìm giá trị lớn nhất, giá trị nhỏ nhất của P = |2z + 1 + 2i|.
A. maxP = 8; minP = √39.
B.maxP = 10; minP = √39.
C. maxP = 8; minP = 6.
D. max P = 10; minP = 6
Lời giải:
Ta có:
Ta chỉ cần tìm GTLN, GTNN của
Ta thấy z1 = 1 - 3i; z2 = -2 + i và z0 =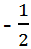 
-i
Do đó max P = 8; min P = √39 .
Đáp án cần chọn là:A
Câu 27. Cho số phức z thỏa mãn:
Gọi M vàm n lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của |z| . Tính M.n.
A. 2.
B. 1.
C. 2√2.
D. 2√3.
Lời giải:
Suy ra quỹ tích điểm biểu diễn số phức z là elíp có tiêu điểm và độ dài trục lớn là 2a = 4 và tiêu cự 2c = 2√2.
Khi đó:
Đáp án cần chọn là:C
Câu 28. Cho số phức z = a + bi, (a ≥ 0; b ≥ 0; a, b ∈ R). Đặt f(x) = ax2 + bx - 2. Biết:
Tính giá trị lớn nhất của |z| .
A. max|z| = 2√5
B. max|z| = 3√2
C. max|z| = 5
D. max|z| = 2√6
Lời giải:
Từ giả thiết ta có:
Xét trên hệ tọa độ Oxy các đường thẳng
d: x - y - 2 = 0; d’: x + 4y - 12 = 0 và các trục tọa độ
+ Đường thẳng d ∩ Ox = A(2; 0); d ∩ Oy = (0; -2) = B; d' ∩ Ox = C(12; 0) và hai đường thẳng d ∩ d' = I(4; 2)
+ Miền nghiệm của (I) được biểu diễn trên mặt phẳng tọa độ nằm trong tứ giác OAID kể cả các điểm thuộc trên các cạnh của đa giác.
+ Ta có: |z|2 = a2 + b2 = OM2, |z| lớn nhất khi và chỉ khi OM lớn nhất hay OM2 lớn nhất với M(a; b) là điểm thuộc miền đa giác lồi OAID.
+ Ta có: OA = 2; OI = 2√5; OD = 3. Từ đó suy ra max|z| = 2√5
Dấu bằng diễn ra khi và chỉ khi z = 4 + 2i.
Đáp án cần chọn là:A
Câu 29. Tập hợp các điểm biểu diễn số phức z thỏa
A. Một parabol.
B. Một điểm.
C. Một đường thẳng.
D. Một đường tròn.
Lời giải:
Giả sử z = x + yi, (x, y ∈ R), khi đó ta có: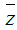 
= x - yi
Từ đó ta được:
Vậy quỹ tích cần tìm là đường parabol.
Đáp án cần chọn là:A
Câu 30. Trong mặt phẳng tọa độ Oxy, gọi H là phần mặt phẳng chứa các điểm biểu diễn của các số phức z thỏa mãn 
và 
có phần thực và ảo đều thuộc [0; 1] . Tính diện tích của H
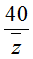
A. 1600.
B. 400π.
C. 50(3 - π).
D. 1200- 200π .
Lời giải:
+ Giả sử z = x + yi, (x, y ∈ R), khi đó:
theo bài ta có: 0 ≤ x ≤ 40; 0 ≤ y ≤ 40.
Từ đó ta thấy điểm biểu diễn M cho các số phức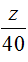 
là hình vuông có OABC như hình vẽ.
Theo bài ta có:
Từ (1) ta được x ≥ 0 và x2 + y2 ≥ 40x <=> (x - 20)2 + y2 ≥ 400 (1').
Từ (2) ta được y ≥ 0 và x2 + y2 ≥ 40y <=> x2 + (y - 20)2 ≥ 400 (2')
Tập hợp các điểm biểu diễn cho miền (H) là nằm trong miền “màu đỏ” ta cần tính diện tích của miền này.
+ Diện tích của một phần bốn cung tròn có bán kính R = 20 là:
Nên diện tích hình hoa văn tạo bởi cung AIO và cung OIC là S* = 100π + 202 + 100π = 400 + 200π và diện tích cần tính bằng: S = 402 - S* = 1200 - 200π.
Đáp án cần chọn là:D
Câu 31. Cho hai số phức z1, z2 thỏa mãn |z1| = 2, |z2| = √3 và nếu gọi M, N lần lượt là điểm biểu diễn cho các số phức z1; z2 thì:
A. P = √5.
B. P = 4√7.
C. P = 3√3.
D. P = 5√2.
Lời giải:
Ta có:
Từ đó ta có: P = |z1 - 2iz2|.|z1 + 2iz2|.
Theo bài gọi điểm biểu diễn cho số phức 2iz là A khi đó N là trung điểm của đoạn OA.
Ta có:
|z1 - 2iz| = MA, theo định lý cô sin cho tam giác OMA ta có:
MA2 = OM2 + OA2 - 2OM.OA.cos30o = 4 + 4.4 - 2.2.2√3.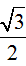
= 4
Từ đó ta được MA = 2.
Nếu đặt z1 = a + bi; z2 = x + yi, (a, b, x, y ∈ R), ta có:
Q = 16 + 2i[(x + yi)(a - bi) - (a + bi)(x - yi)] = 16 + 2i(-2bxi + 2ayi) = 16 + 4(bx - ay)
Ta có: iz2 = -y + xi nên ta có:
Từ đó ta được Q = 16 + 4.3 = 28, từ đó suy ra |z1 + 2iz2| = 2√7. Từ đó ta được P = 4√7.
Đáp án cần chọn là:B
Câu 32. Trong mặt phẳng phức Oxy, tập hợp các điểm biểu diễn số phức z thỏa mãn:
là hai đường thẳng d1 ; d2. Khoảng cách giữa 2 đường thẳng d1 ; d2 là bao nhiêu?
A. d(d1 ; d2) = 2.
B. d(d1 ; d2) = 4.
C. d(d1 ; d2) = 1.
D. d(d1 ; d2) = 6.
Lời giải:
Gọi M(x; y) là điểm biểu diễn số phức z = x + yi
Ta có:
⇔ |x2 + 2xyi - y2 + x2 - 2xyi - y2 + 2x2 + 2y2| = 16
⇔ | 4x2| = 16 ⇔ x = ± 2
=< d(d1 ; d2)=4.
Đáp án cần chọn là:B
Câu 33. Cho số phức z thỏa mãn điều kiện |z - 1| = √2. Tìm giá trị lớn nhất của T = | z + i| + |z - 2 - i|
A. max T = 8√2.
B. max T = 4 .
C. max T = 4√2.
D. maxT = 8 .
Lời giải:
T = | z + i| + |z - 2 - i| = |(z - 1) + (1 + i)| + |(z - 1) - (1 + i)|
Đặt w = z - 1. Ta có |w| = 1 và T = |w + (1 + i)| + |w - (1 + i)|
Đặt w = x + yi . Khi đó |w|2 = 1 = x2 + y2
Vậy maxT = 4 .
Đáp án cần chọn là:B
Câu 34. Cho số phức z thoả mãn:
Giá trị lớn nhất của biểu thức P = |z - 5 - 2i| bằng
A. √2 + 5√3
B. √2 + 3√5
C. √5 + 2√3
D. √5 + 3√2
Lời giải:
Cách 1: Đại số
Đặt z = a + bi.
Từ giả thiết
Dễ thấy P lớn nhất khi ab ≤ 0.
Khi đó :
Do a;b ≤ 0 nên từ (1) ta có (a + 1)2 + (b + 1)2 = 2.
Suy ra
Dấu "=" xảy ra khi
Chọn B.
Cách 2: Hình học
Đặt z = a + bi.
Từ giả thiết
Tập hợp M biểu diễn z thuộc các phần đường tròn cùng bán kính là R = √2 có tâm là A(-1;1); B(1;1); C(1;-1); D(-1; -1) nằm chọn vẹn trong 1 góc phần tư (bỏ đi các cung nhỏ).
P = ME với E(5;2). Từ hình vẽ ta thấy max P = HE = ED + radic;2 = 3√5 + √2 .
Đáp án cần chọn là:B
Câu 35. Cho phương trình: ( z2-z) ( z+3) (z+ 2) =10 . Tính tổng tất cả các phần thực của các nghiệm phương trình trên..
A. -1
B. -2
C. -3
D. -4
Lời giải:
Phương trình đã cho tương đương với phương trình
Z( z+ 2) ( z-1) ( z+ 3)
Hay ( z2+ 2z) ( z2+ 2z-3) = 10
Đặt t= z2+ 2z. Khi đó phương trình trở thành: t2-2t-10= 0.
Tổng tất cả các phần thực của các nghiệm phương trình đã cho là :
-1+ ( -1) + (-1) + ( -1) = -4.
Đáp án cần chọn là:D
Câu 36. Cho A; B; C tương ứng là các điểm trong mặt phẳng phức biểu diễn các số phức
Z1=1+2i; z1=-2+5i ; z1=2+4i . Số phức z biểu diễn bởi điểm D sao cho tứ giác ABCD là hình bình hành là
A. -1+7i.
B. 5+i.
C. 1+5i.
D.3+5i.
Lời giải:
Đáp án cần chọn là:B
Câu 37. Cho 3 điểm A ; B ;C lần lượt biểu diễn cho các số phức z1 ; z1 ; z1 .Biết |z1|= |z2|=|z3| và z1+ z2= 0 . Khi đó tam giác ABC là tam giác gì?
A. Tam giác ABC đều.
B. Tam giác ABC vuông tại C.
C. Tam giác ABC cân tại C.
D. Tam giác ABC vuông cân tại C
Lời giải:
Vì z1+ z2= 0 nên z1 ; z2 là hai số phức đối nhau, do đó hai điểm A: B đối xứng qua gốc O ( tức O là trung điểm của đoạn thẳng AB).
Vậy tam giác ABC có độ dài đường trung tuyến bằng một nửa cạnh huyền nên vuông tại C .
Đáp án cần chọn là:B
Câu 38. Tập hợp các điểm trong mặt phẳng tọa độ biểu diễn số phức z thoả mãn điều kiện:
là hình gì?
A. Một đường thẳng.
B. Một đường Parabol.
C. Một đường Elip.
D. Một đường tròn.
Lời giải:
Quỹ tích các số phức z là một đường Parabol.
Đáp án cần chọn là:B
Câu 39. Gọi M là điểm biểu diễn của số phức z thỏa mãn 
. Tập hợp tất cả những điểm M như vậy là
A. một parabol.
B. một đường thẳng.
C. một đường tròn.
D. một elip
Lời giải:
Gọi số phức z=x+yi có điểm biểu diễn là M(x;y) trên mặt phẳng tọa độ:
Theo đề bài ta có:
Đáp án cần chọn là:A
Câu 40. Xác định tập hợp các điểm M trong mặt phẳng phức biểu diễn các số phức z thỏa mãn điều kiện
A. Là đường Hyperbol.y=-1/x
B. Là đường Hyperbol.y=1/x
C. Là đường tròn tâm 0 bán kính R=4.
D. Là hai đường Hyperbol y=-1/x và y=1/x
Lời giải:
Gọi M(x; y) là điểm biểu diễn số phức z=x+yi
Đáp án cần chọn là:D
Câu 41. Có bao nhiêu số phức z thỏa mãn |z|= √(2 ) và z2 là số thuẩn ảo.
A. 2
B. 3
C. 4
D. 5
Lời giải:
Đặt z= x+ yi
Vậy các số phức cần tìm là: z= 1+ i; z= 1-i; z= -1 + i và z= -1- i ..
Đáp án cần chọn là:C
Câu 42. Tính tổng phần ảo các số phức z thỏa mãn |z|= 5 và phần thực của nó bằng 2 lần phần ảo.
A. 0
B. 1
C. 2
D.3
Lời giải:
Gọi số phức cần tìm là z= x= yi.
Ta có:
Đáp án cần chọn là:A
Câu 43. Cho số phức z thỏa mãn ( 1- 3i) z là số thực và |z−-2+5i|=1. Hỏi có bao nhiêu số phức z thỏa mãn
A. 1
B. 2
C. 3
D. 4
Lời giải:
Gọi số phức cần tìm là z = a+ bi .
Ta có ( 1-3i) z= ( 1-3i) ( a+ bi)
= a+ 3b- 3ai + bi= a+ 3b+ ( b- 3a) i
+Do ( 1-3i) z là số thực nên b- 3a= 0 hay b= 3a
+ ta có |z−-2+5i|=1⇔|a-2+(-b+5)i|=1
Hay ( a-2) 2+ ( 5- 3a) 2= 1
Vậy có hai số phức z thỏa mãn là z= 2+ 6i và z= 7/5+ 21/5 i
Đáp án cần chọn là:B
Câu 44. Tìm số phức z biết |iz +1 | =√(2 ) và ( 1+ i) z+ 1 – 2i là số thuần ảo
A. z= 1
B. z= 1+ 2i
C. z= - 1 và z= 1+ 2i
D. Đáp án khác
Lời giải:
Đáp án cần chọn là:C
Câu 45. Biết z1; z1 là số phức thỏa mãn 
Tính z12; z22
A.-111/4+ i
B. -111+ i
C.-111+ 4i
D. -44+ i
Lời giải:
Gọi z= a+ bi
Ta được: ( a+ bi+ 1) 2+ |a+b i-1| 2 + 10i = a- bi + 3
Tương đương: ( 2a 2-a-1) + ( 2ab+ 3b+ 10) i = 0
Đáp án cần chọn là:A
Câu 46. Biết z1; z2 là số phức thỏa điều kiện 
A. –i
B. i
C. 1+ i
D. 0
Lời giải:
Đáp án cần chọn là:D
Câu 47. Cho phương trình z2+ mz-6i=0 Để phương trình có tổng bình phương hai nghiệm bằng 5 thì m có dạng m= ± ( a+ bi) . Giá trị a+2b là:\
A.0
B. 1
C.- 2
D. - 1
Lời giải:
Gọi z1; z1 là hai nghiệm của phương trình đã cho
Theo bài cho, tổng bình phương hai nghiệm bằng 5. Ta có:
z12+ z22 = S2- 2P= m2+ 12i= 5
Suy ra: m2= 5- 12i
Do đó; m= ±( 3-2i)
Vậy a= 3 ; b= -2 và a+ 2b= -1
Đáp án cần chọn là:D
Câu 48. Trong tập số phức, giá trị của m để phương trình bậc hai z2+ mz+ i= 0 có tổng bình phương hai nghiệm bằng -4i là:
A.±( 1-i)
B.1-i
C.±( 1+ i)
D. -1-i
Lời giải:
Gọi z1; z2 là hai nghiệm của phương trình.
Đáp án cần chọn là:A
Câu 49. Gọi z1 ; z2 là hai nghiệm của phương trình z2+ 2z+ 8= 0, trong đó z1 có phần ảo dương. Giá trị của số phức 
A. 12+6i
B. 10
C. 8
D.12- 6i
Lời giải:
Đáp án cần chọn là:C
Câu 50.
Cho z1; z2; z3; z4 là các nghiệm của phương trình: ( z2+1) ( z2-2z+ 2) = 0 . Tính s=z12014 +z22014+ z32014+ z42014
A.5
B.4
C.-2
D.3
Lời giải:
Đáp án cần chọn là:C
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.
