Toptailieu.vn xin giới thiệu 50 bài tập trắc nghiệm Phép chia số phức (có đáp án) chọn lọc, hay nhất giúp học sinh lớp 12 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán.

Mời các bạn đón xem:

Phép chia số phức

Câu 1: Số phức

A. -1+i

B.1-i

C. -1-i

D. 1+5i.

Lời giải:

Ta có

Đáp án cần chọn là:A

Câu 2: Số phức z thỏa mãn z(1 + 2i) + 1 - i = 2i là

A. -1+i 

B. 1-i

C. 1+i

D. -1-i.

Lời giải:

Ta có:z(1 + 2i) + 1 - i = 2i là <=> z(1 + 2i) = -1 + 3i

Do đó:

 

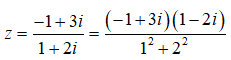
Đáp án cần chọn là:C

Câu 3: Phần thực và phần ảo của số phức

A. 0 và 1

B. 0 và i

C. 0 và -1

D. 0 và – i.

Lời giải:

Ta có

Vậy phần thực và phần ảo của z là 0 và -1

Đáp án cần chọn là:C

Câu 4: Cho số phức

Phần thực và phần ảo của số phức w = (z + 1)(z + 2) là

A. 2 và 1

B. 1 và 3

C. 2 và i

D. 1 và 3i.

Lời giải:

Ta có

Suy ra w = (z + 1)(z + 2) = (i + 1)(i + 2) = -1 + 2i + i + 2 = 1 + 3i

Vậy phần thực và phần ảo của w là 1 và 3

Đáp án cần chọn là:B

Câu 5: Các số thực x, y thỏa mãn

Khi đó, tổng T = x + y bằng

A. 4

B.5

C. 6

D. 7.

Lời giải:

Ta có

Vậy T = -2 + 8 = 6

Đáp án cần chọn là:C

Câu 6: Cho số phức z thỏa mãn (3 + 2i)z + (2 - i)² = 4 + i. Môđun của số phức w = (z + 1)z− là

A. 2

B. 4

C. 10

D. √10

Lời giải:

Ta có:

Đáp án cần chọn là:D

Câu 7: Cho số phức z thỏa mãn 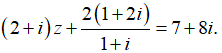 Môđun của số phức w = z + i + 1 là

A. 3

B. 4

C. 5

D. 6.

Lời giải:

Đáp án cần chọn là:C

Câu 8. Cho số phức z thỏa z=(1-i/1+i)²⁰¹⁶Viết z dưới dạng z=a+bi. Khi đó tổng a+b có giá trị bằng bao nhiêu?

A.3

B.-1

C. 1.

D. 2.

Lời giải:

Đáp án cần chọn là:C

Câu 9. Tìm phần thực của số phức 

A. 3/ 5

B. 8/5

C. 6/5

D. Đáp án khác

Lời giải:

Đáp án cần chọn là:C

Câu 10. Tìm phần thực a của số phức z thỏa mãn (1+ i) 2( 2-i) z= 8+ i+ (1+ 2i) z.

A.a=2

B.a= -3

C.a=-2.

D.a=3

Lời giải:

Ta có: (1+ i) 2( 2-i) z= 8+ i+ (1+ 2i) z.

Suy ra: (2+4i)z-(1+2i)z=8=i

Vậy phần thực của z bằng 2.

Đáp án cần chọn là:A

Câu 11. Cho số phức 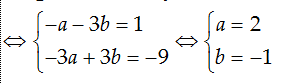 Tìm phần thực a và phần ảo b của số phức X−

A.a=2; b=6

B. a=-2; b= -6

C.a=-2; b=6

D. a=2; b= -3

Lời giải:

Đáp án cần chọn là:C

Câu 12. Cho số phức thỏa mãn điều kiện 

A. 10.

B.-10 .

C. 100.

D.-100 .

Lời giải:

Suy ra w= 1+ 2z+ z²= ( 1+ z) ²= ( 3-i) ²= 8-6i nên modul của w=10.

Đáp án cần chọn là:A

Câu 13. Cho số phức z thỏa mãn điều kiện:(1+i) z−-1-3i=0. Phần ảo của số phức

w=1-iz+z là

A. 1.

B. -3

C.-2 .

D. -1 .

Lời giải:

Vậy z= 2-i và w= 1-iz+ z= 1- i( 2-i) + 2-i= 2-3i

Phần ảo của w là -3

Đáp án cần chọn là:B

Câu 14. Tìm phần thực, phần ảo của số phức z thỏa ( z/2 – 1) ( 1-i) = ( 1+ i) ³⁹⁷⁹

A. Phần thực là 2¹⁹⁹⁰ và phần ảo là 2.

B. Phần thực là - 2¹⁹⁹⁰ và phần ảo là 2.

C. Phần thực là -2¹⁹⁸⁹ và phần ảo là 1.

D. Phần thực là 2¹⁹⁸⁹ và phần ảo là 1

Lời giải:

Ta có

Đáp án cần chọn là:B

Câu 15. Cho số phức z= 1+ ( 1+ i) + ( 1+i) ²+ ...+ (1+ i) ²⁶ . Phần thực của số phức z là

A. 2¹³

B.-( 1+ 2¹³)

C.- 2¹³

D. 1+ 2¹³

Lời giải:

Số phức z là tổng của cấp số nhân với số hạng đầu là 1 và công bội q=1+i.

Do đó :

Vậy phần thực là 2¹³

Đáp án cần chọn là:A

Câu 16. Giải các phương trình sau đây ( 2+ i) z= z+ 2i-1

A. z= 1+ i

B.. z= 0,5+ 1,5 i

C. z= 2+ i

D. Đáp án khác

Lời giải:

Gọi M(x; y) là điểm biểu diễn của số phức w trên mặt phẳng Oxy. Khi đó tập hợp điểm biểu diễn của số phức z là đường tròn tâm I( 0; -1), bán kính r= 1.

Đáp án cần chọn là:B

Câu 17. Cho các số phức z thỏa mãn |z-2-4i|=2. Gọi z₁; z₂ số phức có module lớn nhất và nhỏ nhất. Tổng phần ảo của hai số phức bằng?

A.8i

B. 4

C. -8

D. 8.

Lời giải:

Đáp án cần chọn là:D

Câu 18. Cho số phức z thỏa mãn 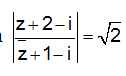Tìm giá trị nhỏ nhất và giá trị lớn nhất của modul z lần lượt là .

A. √10-1; √(10 )+3

B. √10-3; √(10 )+3

C. √10-1; √(10 )+1

D. √10; √(10 )+3

Lời giải:

Giả sử z= x+ yi. Từ giả thiết:

Đáp án cần chọn là:A

Câu 19. Cho số phức 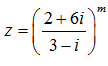m nguyên dương. Có bao nhiêu giá trị 1≤ m≤ 50 để z là số thuần ảo?

A. 26

B. 25.

C. 24.

D. 50.

Lời giải:

Đáp án cần chọn là:B

Câu 20. Tìm mô-đun của số phức w= b+ ci biết số phức 

là nghiệm của phương trình z2+ 8bz+ 64c= 0 .

A.2√5

B. 7

C.√29

D.√19

Lời giải:

Đáp án cần chọn là:C

Câu 21. Cho số phức z thỏa mãn (z+i)/(z-i) là số thuần ảo. Tập hợp các điểm M biểu diễn số phức z là:

A. Đường tròn tâm O, bán kính R=1.

B. Hình tròn tâm O, bán kính R=1 (kể cả biên).

C. Hình tròn tâm O, bán kính R=1 (không kể biên).

D. Đường tròn tâm O, bán kính R=1 bỏ đi một điểm (0;1)

Lời giải:

Đáp án cần chọn là:D

Câu 22. Cho a,b,c là 3 số phức phân biệt khác 0 và modul của chúng bằng nhau . Nếu một nghiệm của phương trình az2+ bz+ c = 0 có môđun bằng 1 thì khẳng định nào sau đây đúng

A. c²= ab

B. a²= bc

C. b= ac

D. b²= ac

Lời giải:

Đáp án cần chọn là:D

Câu 23. Tìm số phức z biết |iz +1 | =√(2 ) và ( 1+ i) z+ 1 – 2i là số thuần ảo

A. z= 1

B. z= 1+ 2i

C. z= - 1 và z= 1+ 2i

D. Đáp án khác

Lời giải:

Đáp án cần chọn là:C

Câu 24. Tìm số nguyên dương n bé nhất để(√3+i/1-i) ³ là số thực.

A. 6

B. 12

C. 10

D. 24

Lời giải:

Đáp án cần chọn là:B

Câu 25. Tính giá trị của biểu thức sau.

A. -8

B. - 12

C. – 16

D. -18

Lời giải:

Đáp án cần chọn là:A

Câu 26. Biểu thức sau có modul bằng bao nhiêu

A. 1

B. 2

C. 3

D. 4 .

Lời giải:

Đáp án cần chọn là:A

Câu 27. Tìm modul của biểu thức sau.

A. 2

B. 4

C. 1

D. 3

Lời giải:

Đáp án cần chọn là:C

Câu 28. Cho z₁; z₂ là hai nghiệm phức của phương trình z²- 2z+ 4= 0. Tìm phần thực, phần ảo của số phức:w=(z₁/z₂)²⁰¹³ lần luợt là bao nhiêu, biết z₁ có phần ảo dương.

A. 0; 1

B. 1;2

C. 1; 0

D. tất cả sai

Lời giải:

Vậy phần thực bằng 1, phần ảo bằng 0.

Đáp án cần chọn là:C

Câu 29. Cho các số phức z thỏa mãn: ( 2-z) ⁵= z⁵. Hỏi phần thực của z là bao nhiêu?

A. 0

B.1

C. 2

D. Chưa kết luận được

Lời giải:

Vậy z luôn có phần thực là 1.

Đáp án cần chọn là:B

Câu 30. Cho phương trình 8z²-4( a+ 1) z+ 4a+1= 0 (1) với a là tham số. Tính tổng tất cả các giá trị của a để (1) có hai nghiệm z₁ ; z₂ thỏa mãn z₁/ z₂ là số ảo, trong đó z₂ là số phức có phần ảo dương.

A. 1

B. 2

C. 3

D. 4

Lời giải:

Từ giả thiết suy ra z₁; z₂ không phải là số thực.

Do đó , hay 4( a+1)²-8( 4a+1) < 0

Hay a2-6a-1< 0

Tương đương: ( a+1) ²-( - ( a²-6a-1) ) = 0 hay a²-2a= 0

Vậy a= 0 hoặc a= 2.

Đối chiếu với điều kiện (*) ta có giá trị của a là a= 0 hoặc a= 2 .

Đáp án cần chọn là:B

Câu 31: Số phức 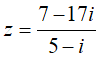 có phần thực là

A. 2.

B.  .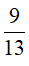

C. 3.

D. -3 .

Lời giải:

=> phần thực của z là 2

Đáp án cần chọn là:A

Câu 32:Phần thực, phần ảo của số phức z thỏa mãn 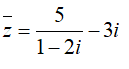 lần lượt là

A. 1;1.

B.1;-2 

C. 1;2.

D.1;-1

Lời giải:

Phần thực, phần ảo của z lần lượt là 1;1.

Đáp án cần chọn là:A

Câu 33: Cho số phức z thỏa mãn điều kiện:(1 + i)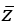 - 1 - 3i = 0. Phần ảo của số phứcw = 1 - iz + z là

A. 1.

B. -3.

C. -2.

D. -1.

Lời giải:

Phần ảo của w là -3

Đáp án cần chọn là:B

Câu 34:Tìm phần thực, phần ảo của số phức z thỏa 

A. Phần thực là 2¹⁹⁹⁰ và phần ảo là 2.

B. Phần thực là -2¹⁹⁹⁰ và phần ảo là 2.

C. Phần thực là -2¹⁹⁸⁹ và phần ảo là 1.

D. Phần thực là 2¹⁹⁸⁹ và phần ảo là 1

Lời giải:

Ta có:

Đáp án cần chọn là:B

Câu 35:Cho số phức z = 1 + (1 + i) + (1 + i)² + ...+ (1 + i)²⁶ . Phần thực của số phức z là

A. 2¹³

B. -(1 + 2¹³)

C. -2¹³

D. (1 + 2¹³)

Lời giải:

Số phức z là tổng của cấp số nhân với số hạng đầu là 1 và công bội q = 1 + i. Do đó :

Vậy phần thực là 2¹³

Đáp án cần chọn là:A

Câu 36: Cho số phức 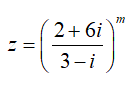 , m nguyên dương. Có bao nhiêu giá trị m ∈ [1;50] để z là số thuần ảo?

A. 26.

B. 25.

C. 24.

D. 50.

Lời giải:

Z là số thuần ảo khi và chỉ khi m = 2k + 1

Mà

Với 25 giá trị của k cho ta tương ứng 25 giá trị m thỏa yêu cầu đề bài.

Đáp án cần chọn là:B

Câu 37:Cho số phức Tìm 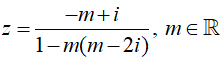 |z|_max

A.  .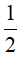

B. 0.

C. 1.

D. 2.

Lời giải:

Ta có:

Đáp án cần chọn là:A

Câu 38: Tìm phần thực của số phức 25i/z , biết rằng .z/2-i+(4-3i)z−= 26+6i

A. 3

B. -2

C. – 4

D. 5

Lời giải:

Gọi số phức cần tìm là z= a+ bi .

Ta có

Vậy phần thực là -4, phần ảo là 3.

Đáp án cần chọn là:C

Câu 38: Cho số phức z thỏa z=(1-i/1+i)²⁰¹⁶Viết z dưới dạng z=a+bi. Khi đó tổng a+b có giá trị bằng bao nhiêu?

A.3

B.-1 .

C. 1.

D. 2.

Lời giải:

Đáp án cần chọn là:C

Câu 39: Cho 2 số phức 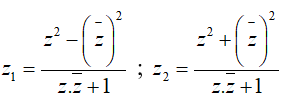 với z = x + yi, x,y ∈ R .

Mệnh đề nào sau đây đúng?

A.z₁ và z₂ là số thuần ảo.

B. z₂ là số thuần ảo.

C. z₁ là số thuần ảo.

D. z₁ và z₂ là số thực

Lời giải:

Khi đó : 

Suy ra z₁ là số thuần ảo; z₂là số thuần thực.

Đáp án cần chọn là:C

Câu 40: Cho số phức z thỏa 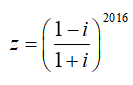 . Viết z dưới dạng z = a + bi. Khi đó tổng a+b có giá trị bằng bao nhiêu?

A.3

B. -1

C. 1.

D. 2.

Lời giải:

Đáp án cần chọn là:C

Câu 41: Cho số phức z thỏa mãn điều kiện |z - 3 + 4i| ≤ 2. Trong mặt phẳng Oxy tập hợp điểm biểu diễn số phức w = 2z + 1 - i là hình tròn có diện tích:

A. S = 9π

B. S = 12π.

C. S = 16π.

D.S = 25π.

Lời giải:

Ta có:

<=> |w - 1 + i - 6 + 8i| ≤ 4 <=> |w - 7 + 9i| ≤ 4 (1)

Giả sử w = x + yi, khi đó (1) <=> (x - 7)² + (y + 9)² ≤ 16

Suy ra tập hợp điểm biểu diễn số phức w là hình tròn tâm I(7; -9), bán kính r = 4

Vậy diện tích cần tìm là S = π.4² = 16π

Đáp án cần chọn là:C

Câu 42: Cho số phức z thỏa mãn |z| = 1. Tìm giá trị lớn nhất của biểu thức

A.5

B.4

C.6

D.8

Lời giải:

Ta có:

Khi z = i thì A = 6

Đáp án cần chọn là:C

Câu 43. Cho số phức z thỏa mãn |z| = 1. Tìm giá trị lớn nhất max M và giá trị nhỏ nhất min M của biểu thức M = |z² + z + 1| + |z³ + 1|

A. max M = 5; min M = 1

B. max M = 5; min M = 2

C. max M = 4; min M = 1

D.max M = 4; min M = 2

Lời giải:

Ta có: M ≤ |z|² + |z| + 1 + |z|³ + 1 = 5 ,

khi z = 1 thì M = 5 nên max M = 5

Mặt khác:

khi z = -1 thì M = 1 nên min M = 1

Đáp án cần chọn là:A

Câu 44. Cho z₁; z₂ là hai số phức liên hợp của nhau và thỏa mãn 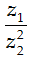 ∈ R và |z₁ - z₂| = 2√3. Tính môđun của số phức z₁.

A. |z₁| = √5

B. |z₁| = 3

C. |z₁| = 2

D. |z₁| =

Lời giải:

Gọi z₁ = a + bi; z₂ = a - bi.

Không mất tính tổng quát ta coi b ≥ 0

Do |z₁ - z₂| = 2√3 => |2bi| = 2√3 => b = √3

Do z₁; z₂ là hai số phức liên hợp của nhau nên z₁; z₂ ∈ R, mà:

Ta có:

(z₁)³ = (a + bi)³ = (a³ - 3ab²) + (3a²b - b³)i ∈ R

Đáp án cần chọn là:C

Câu 45. Biết số phức z thỏa mãn đồng thời hai điều kiện |z - 3 - 4i| = √5 và biểu thức M = |z + 2|² - |z - i|² đạt giá trị lớn nhất. Tính môđun của số phức z + i.

A. |z + i| = 2√41

B. |z + i| = 3√5

C. |z + i| = 5√2

D. |z + i| = √41

Lời giải:

Gọi z = x + yi.

Ta có: |z - 3 - 4i| = √5 <=> (C): (x - 3)² + (y - 4)² = 5, tâm I(3; 4) và R = √5

Mặt khác:

M = |z + 2|² - |z - i|² = (x + 2)² + y² - [(x²) + (y - 1)²] = 4x + 2y + 3

<=> d: 4x + 4y + 3 - M = 0

Do số phức z thỏa mãn đồng thời hai điều kiện nên d và (C) có điểm chung

Đáp án cần chọn là:D

Câu 46. Cho số phức z thỏa mãn 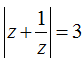. Tổng giá trị lớn nhất, nhỏ nhất của |z| là:

A. 3

B. √5

C. √13

D. 5

Lời giải:

Với giả thiết ta có:

Từ đó ta được:

Từ đó bằng cách thay a cụ thể ta được đáp án C.

Đáp án cần chọn là:C

Câu 47. Cho số phức z thỏa mãn |z| = 1 Tìm tổng giá trị lớn nhất, nhỏ nhất của biểu thức P với P = |1 + z²2| - |1 + z| ?

A. 2 + √2

B. 1 + 2√2

C. -1 + 2√2

D. 2 - √2

Lời giải:

Ta có:

nên ta có maxP = P(1) = 0; minP = P(0) = -√2.

Hàm số nghịch biến trên .

Từ đó ta được max P = P(-1) = 2; minP = P(0) = -√2.

+ Từ trên ta được:

Đáp án cần chọn là:A

Câu 48. Cho số phức z thỏa mãn:

Gọi M vàm n lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của |z| . Tính M.n.

A. 2.

B. 1.

C. 2√2.

D. 2√3.

Lời giải:

Suy ra quỹ tích điểm biểu diễn số phức z là elíp có tiêu điểm và độ dài trục lớn là 2a = 4 và tiêu cự 2c = 2√2.

Khi đó:

Đáp án cần chọn là:C

Câu 49. Cho số phức z thỏa mãn điều kiện |z - 1| = √2. Tìm giá trị lớn nhất của T = | z + i| + |z - 2 - i|

A. max T = 8√2.

B. max T = 4 .

C. max T = 4√2.

D. maxT = 8 .

Lời giải:

T = | z + i| + |z - 2 - i| = |(z - 1) + (1 + i)| + |(z - 1) - (1 + i)|

Đặt w = z - 1. Ta có |w| = 1 và T = |w + (1 + i)| + |w - (1 + i)|

Đặt w = x + yi . Khi đó |w|² = 1 = x² + y²

Vậy maxT = 4 .

Đáp án cần chọn là:B

Câu 50. Trong C, phương trình z+1/z=2i có nghiệm là:

A.(1±√3)i

B. (5±√2)i

C. (1±√2)i

D.(2±√(5)i)

Lời giải:

Đáp án cần chọn là:A