Khái niệm về thể tích của khối đa diện (Lý thuyết + 50 bài tập có lời giải)

A. Tóm tắt lý thuyết

I. NHẮC LẠI MỘT SỐ ĐỊNH NGHĨA

    • Hình lăng trụ là hình có hai đáy là hai đa giác bằng nhau nằm trên hai mặt phẳng song song với nhau và các mặt bên đều là các hình bình hành.

1. Hình lăng trụ đứng

    Định nghĩa. Hình lăng trụ đứng là hình lăng trụ có cạnh bên vuông góc với mặt đáy.

    Tính chất. Các mặt bên của hình lăng trụ đứng là các hình chữ nhật và vuông góc với mặt đáy.

2. Hình lăng trụ đều

    Định nghĩa. Hình lăng trụ đều là hình lăng trụ đứng có đáy là đa giác đều.

    Tính chất. Các mặt bên của hình lăng trụ đều là các hình chữ nhật bằng nhau và vuông góc với mặt đáy.

    • Hình hộp là hình lăng trụ có đáy là hình bình hành.

1. Hình hộp đứng

    Định nghĩa. Hình hộp đứng là hình hộp có cạnh bên vuông góc với mặt đáy.

    Tính chất. Hình hộp đứng có 2 đáy là hình bình hành, 4 mặt xung quanh là 4 hình chữ nhật.

2. Hình hộp chữ nhật

    Định nghĩa. Hình hộp chữ nhật là hình hộp đứng có đáy là hình chữ nhật.

    Tính chất. Hình hộp chữ nhật có 6 mặt là 6 hình chữ nhật.

3. Hình lập phương

    Định nghĩa. Hình lập phương là hình hộp chữ nhật 2 đáy và 4 mặt bên đều là hình vuông

    Tính chất. Hình lập phương có 6 mặt đều là hình vuông.

    • Hình chóp là hình có đáy là một đa giác và các mặt bên là các tam giác có chung một đỉnh.

II. THỂ TÍCH

1. Công thức tính thể tích khối chóp

    Trong đó: S là diện tích đáy, h là chiều cao khối chóp.

2. Công thức tính thể tích khối lăng trụ

    Trong đó: B là diện tích đáy, h là hiều cao khối lăng trụ

    ● Thể tích khối hộp chữ nhật: V = abc

    Trong đó: a, b, c là ba kích thước của khối hộp chữ nhật.

    ● Thể tích khối lập phương: V = a3

    Trong đó a là độ dài cạnh của hình lập phương.

III. TỈ SỐ THỂ TÍCH

    Cho khối chóp S.ABC và A', B', C' là các điểm tùy ý lần lượt thuộc SA, SB, SC ta có

 

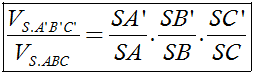
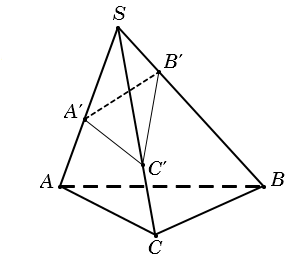
    Phương pháp này được áp dụng khi khối chóp không xác đinh được chiều cao một cách dễ dàng hoặc khối chóp cần tính là một phần nhỏ trong khối chóp lớn và cần chú ý đến một số điều kiện sau

    - Hai khối chóp phải cùng chung đỉnh.

    - Đáy hai khối chóp phải là tam giác.

    - Các điểm tương ứng nằm trên các cạnh tương ứng.

B. Bài tập trắc nghiệm

Câu 1.​​ Cho hình chóp​​ S.ABCD​​ có đáy​​ ABCD​​ là hình vuông cạnh​​ a, cạnh bên​​ SA​​ vuông góc với mặt phẳng đáy và​​ SA=a2.​​ Tính thể tích​​ V​​ của khối chóp​​ S.ABCD.​​ 

A.​​ V=a326.​​  B.​​ V=a324.​​  C.​​ V=a32.​​  D.​​ V=a323.​​ 

Câu 2.​​ Cho hình chóp​​ S.ABC​​ có tam giác​​ SBC​​ là tam giác vuông cân tại​​ S,​​ SB=2a​​ và khoảng cách từ​​ A​​ đến mặt phẳng​​ SBC​​ bằng​​ 3a.​​ Tính theo​​ a​​ thể tích​​ V​​ của khối chóp​​ S.ABC.

 A.​​ V=2a3. B.​​ V=4a3.  ​​ ​​ ​​ ​​ ​​ ​​ ​​ ​​ ​​ ​​ ​​ ​​​​  C.​​ V=6a3 D.​​ V=12a3.

Câu 3.​​ (ĐỀ CHÍNH THỨC 2016 – 2017)​​ Cho khối chóp​​ S.ABC​​ có​​ SA​​ vuông góc với đáy,​​ SA=4,  AB=6,  BC=10​​ và​​ CA=8. Tính thể tích​​ V​​ của khối chóp​​ S.ABC.

 A.​​ V=40.​​  B.​​ V=192.​​  C.​​ V=32.​​  D.​​ V=24.

Câu 4.​​ Cho hình chóp​​ S.ABCD​​ có đáy​​ ABCD​​ là hình chữ nhật có cạnh​​ AB=a,​​ BC=2a. Hai mặt bên​​ SAB​​ và​​ SAD​​ cùng vuông góc với mặt phẳng đáy​​ ABCD, cạnh​​ SA=a15​​ .​​ Tính theo​​ a​​ thể tích​​ V​​ của khối chóp​​ S.ABCD.

 A.​​ V=2a3156.​​  B.​​ V=2a3153.​​  C.​​ V=2a315.​​  D.​​ V=a3153.​​ 

Câu 5.​​ Cho hình chóp​​ S.ABCD​​ có đáy​​ ABCD​​ là hình vuông cạnh​​ a. Cạnh bên​​ SA​​ vuông góc với đáy​​ ABCD​​ và​​ SC=a5. Tính theo​​ a​​ thể tích​​ V​​ khối chóp​​ S.ABCD.​​ 

 A.​​ V=a333.​​  B.​​ V=a336.​​  C.​​ V=a33.​​  D.​​ V=a3153.​​ 

Câu 6.​​ Cho hình chóp​​ S.ABC​​ có đáy​​ ABC​​ là tam giác vuông tại​​ B​​ và​​ BA=BC=a. Cạnh bên​​ SA=2a​​ và vuông góc với mặt phẳng đáy. Tính theo​​ a​​ thể tích​​ V​​ của khối chóp​​ S.ABC.

 A. .V=a3..​​  B.​​ V=a332.​​  C.​​ V=a33.​​  D.​​ V=2a33.

Câu 7.​​ Cho hình chóp​​ S.ABCD​​ có đáy là hình thang vuông tại​​ A​​ và​​ B,​​ AB=BC=1,​​ AD=2. Cạnh bên​​ SA=2​​ và vuông góc với đáy. Tính thể tích khối chóp​​ S.ABCD.

 A.​​ V=1.​​  B.​​ V=32.​​  C.​​ V=13.​​  D.​​ V=2.​​ 

Câu 8.​​ Cho hình chóp​​ S.ABC​​ có đáy​​ ABC​​ là tam giác vuông tại​​ A​​ và có​​ AB=a,​​ BC=a3. Mặt bên​​ SAB​​ là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng​​ ABC. Tính​​ theo​​ a​​ thể tích​​ V​​ của khối chóp​​ S.ABC.

 A.​​ V=a3612.​​  B.​​ V=a364.​​  C.​​ V=2a3612.​​  D.​​ V=a366.​​ 

Câu 9.​​ Cho khối chóp​​ S.ABCD​​ có đáy​​ ABCD​​ là hình vuông cạnh​​ a, tam giác​​ SAB​​ cân tại​​ S​​ và nằm trong mặt phẳng vuông góc với mặt đáy,​​ SA=2a. Tính theo​​ a​​ thể tích​​ V​​ của khối chóp​​ S.ABCD.

 A.​​ V=a31512.​​  B.​​ V=a3156.​​  C.​​ V=2a3.​​  D.​​ V=2a33.​​ 

Câu 10.​​ (ĐỀ CHÍNH THỨC 2016 – 2017)​​ Cho hình chóp đều​​ S.ABC​​ có cạnh đáy bằng​​ a, cạnh bên gấp hai lần cạnh đáy. Tính thể tích​​ V​​ của khối chóp đã cho.

 A.​​ V=13 a312.​​  B.​​ V=11 a312.​​  C.​​ V=11 a36.​​  D.​​ V=11 a34.

Câu 11.​​ Cho hình chóp đều​​ S.ABC​​ có cạnh đáy bằng​​ a, cạnh bên bằng​​ a216. Tính theo​​ a​​ thể tích​​ V​​ của khối chóp đã cho.

 A.​​ V=a338.​​  B.​​ V=a3312.​​  C.​​ V=a3324.​​  D.​​ V=a336.

Câu 12.​​ (ĐỀ THỬ NGHIỆM 2016 – 2017)​​ Cho hình chóp​​ S.ABC​​ có đáy​​ ABC​​ là tam giác đều cạnh​​ 2a​​ và thể tích bằng​​ a3. Tính chiều cao​​ h​​ của hình chóp đã cho.​​ 

 A.​​ h=a36.​​  B.​​ h=a32.​​  C.​​ h=a33.​​  D.​​ h=a3.

Câu 13.​​ Cho hình chóp​​ S.ABC​​ có đáy​​ ABC​​ là tam giác vuông cân tại​​ B,​​ AB=a. Cạnh bên​​ SA=a2, hình chiếu của điểm​​ S​​ lên mặt phẳng đáy trùng với trung điểm của cạnh huyền​​ AC. Tính theo​​ a​​ thể tích​​ V​​ của khối chóp​​ S.ABC.

 A.​​ V=a3612.​​  B.​​ V=a364.​​  C.​​ V=2a3612.​​  D.​​ V=a366.

Câu 14.​​ Cho hình chóp​​ S.ABCD​​ có đáy​​ ABCD​​ là hình thoi cạnh bằng​​ 1,​​ góc​​ ABC^=60°.​​ Cạnh bên​​ SD=2.​​ Hình chiếu vuông góc của​​ S​​ trên mặt phẳng​​ ABCD​​ là điểm​​ H​​ thuộc đoạn​​ BD​​ thỏa​​ HD=3HB.​​ Tính thể tích​​ V​​ của khối chóp​​ S.ABCD.

 A.​​ V=524.​​  B.​​ V=1524.​​  C.​​ V=158.​​  D.​​ V=1512.

Câu 15.​​ Cho hình chóp​​ S.ABCD​​ có đáy​​ ABCD​​ là hình vuông cạnh​​ a. Tam giác​​ SAB​​ vuông tại​​ S​​ và nằm trong mặt phẳng vuông góc với đáy. Hình chiếu vuông góc của​​ S​​ trên​​ AB​​ là điểm​​ H​​ thỏa​​ AH=2BH. Tính theo​​ a​​ thể tích​​ V​​ của khối chóp​​ S.ABCD.

 A.​​ V=a326.​​  B.​​ V=a323.​​  C.​​ V=a339.​​  D.​​ V=a329.​​ 

Câu 16.​​ Cho hình chóp​​ S.ABCD​​ có đáy​​ ABCD​​ là hình vuông tâm​​ O, cạnh​​ a. Cạnh bên​​ SA​​ vuông góc với đáy, góc​​ SBD^=600. Tính thể tích​​ V​​ của khối chóp​​ S.ABCD.

 A.​​ V=a3.​​  B.​​ V=a332.​​  C.​​ V=a33.​​  D.​​ V=2a33.​​ 

Câu 17.​​ Cho hình chóp​​ S.ABC​​ có đáy​​ ABC​​ là tam giác vuông tại​​ B,​​ AC=2a,​​ AB=SA=a. Tam giác​​ SAC​​ vuông tại​​ S​​ và nằm trong mặt phẳng vuông góc với đáy​​ ABC. Tính theo​​ a​​ thể tích​​ V​​ của khối chóp​​ S.ABC.

 A.​​ V=a34.​​  B.​​ V=3a34.​​  C.​​ V=a3.​​  D.​​ V=2a33.​​ 

Câu 18.​​ Cho hình chóp​​ S.ABCD​​ có đáy​​ ABCD​​ là hình vuông. Cạnh bên​​ SA=a​​ và vuông góc với đáy; diện tích tam giác​​ SBC​​ bằng​​ a222(đvdt). Tính theo​​ a​​ thể tích​​ V​​ của khối chóp​​ S.ABCD.

 A.​​ V=a3.​​  B.​​ V=a332.​​  C.​​ V=a33.​​  D.​​ V=2a33.​​ 

Câu 19.​​ Cho hình chóp​​ S.ABC​​ có đáy​​ ABC​​ là tam giác vuông cân tại​​ C, cạnh huyền​​ AB​​ bằng​​ 3. Hình chiếu vuông góc của​​ S​​ xuống mặt đáy trùng với trọng tâm của tam giác​​ ABC​​ và​​ SB=142. Tính theo​​ a​​ thể tích​​ V​​ của khối chóp​​ S.ABC.

 A.​​ V=32.​​  B.​​ V=14.​​  C.​​ V=34. D.​​ V=1.

Câu 20.​​ Cho hình chóp đều​​ S.ABCD​​ có cạnh đáy bằng​​ a, cạnh bên hợp với mặt đáy một góc​​ 600. Tính theo​​ a​​ thể tích​​ V​​ của khối chóp​​ S.ABCD.

A.​​ V=a366.​​  B.​​ V=a362. C.​​ V=a363.​​  D.​​ V=a33.​​ 

Câu 21.​​ Cho hình chóp​​ S.ABCD​​ có đáy​​ ABCD​​ là hình chữ nhật với​​ AB=a,​​ AC=5a. Đường thẳng​​ SA​​ vuông góc với mặt đáy, cạnh bên​​ SB​​ tạo với mặt đáy một góc​​ 600. Tính theo​​ a​​ thể tích​​ V​​ của khối chóp​​ S.ABCD.

 A.​​ V=62a3.​​  B.​​ V=42a3.​​  C.​​ V=22a3.​​  D.​​ V=2a3.​​ 

Câu 22.​​ Cho hình chóp​​ S.ABC​​ có đáy​​ ABC​​ là tam giác đều cạnh​​ a,​​ SA​​ vuông góc với mặt phẳng​​ ABC; góc giữa đường thẳng​​ SB​​ và mặt phẳng​​ ABC​​ bằng​​ 600. Tính theo​​ a​​ thể tích​​ V​​ của khối chóp​​ S.ABC.

 A.​​ V=a34.​​  B.​​ V=3a34.​​  C.​​ V=a32.​​  D.​​ V=a3.​​ 

Câu 23.​​ Cho hình chóp​​ S.ABCD​​ có đáy​​ ABCD​​ là hình thoi cạnh​​ a, góc​​ BAD^=1200. Cạnh bên​​ SA​​ vuông góc với đáy​​ ABCD​​ và​​ SD​​ tạo với đáy​​ ABCD​​ một góc​​ 600. Tính theo​​ a​​ thể tích​​ V​​ của khối chóp​​ S.ABCD.

 A.​​ V=a34.​​  B.​​ V=3a34.​​  C.​​ V=a32.​​  D.​​ V=a3.​​ 

Câu 24.​​ Cho hình chóp​​ S.ABCD​​ có đáy​​ ABCD​​ là hình vuông cạnh bằng​​ 1. Hình chiếu vuông góc của​​ S​​ trên mặt phẳng​​ ABCD​​ là trung điểm​​ H​​ của cạnh​​ AB, góc giữa​​ SC​​ và mặt đáy bằng​​ 300. Tính thể tích​​ V​​ của khối chóp​​ S.ABCD.

 A.​​ V=156.​​  B.​​ V=1518.​​  C.​​ V=13.​​  D.​​ V=56.​​ 

Câu 25.​​ Cho hình chóp​​ S.ABCD​​ có đáy​​ ABCD​​ là hình chữ nhật với​​ AC=2a,BC=a. Đỉnh​​ S​​ cách​​ đều các điểm​​ A,B,C.​​ Biết góc giữa đường thẳng​​ SB​​ và mặt phẳng​​ ABCD​​ bằng​​ 60o.​​ Tính theo​​ a​​ thể tích​​ V​​ của khối chóp​​ S.ABCD.​​ 

 A.​​ V=a34.​​  B.​​ V=3a34.​​  C.​​ V=a32.​​  D.​​ V=a3.​​ 

Câu 26.​​ Cho hình chóp​​ S.ABC​​ có đáy​​ ABC​​ là tam giác vuông cân tại​​ A,​​ AB=AC=a. Cạnh bên​​ SA​​ vuông góc với đáy​​ ABC. Gọi​​ I​​ là trung điểm của​​ BC,​​ SI​​ tạo với mặt phẳng​​ ABC​​ góc​​ 600.​​ Tính theo​​ a​​ thể tích​​ V​​ của khối chóp​​ S.ABC.

 A.​​ V=a364.​​  B.​​ V=a366.​​  C.​​ V=a32.​​  D.​​ V=a3612.​​ 

Câu 27.​​ Cho hình chóp​​ S.ABC​​ có đáy​​ ABC​​ là tam giác đều cạnh​​ a, hình chiếu vuông góc của đỉnh​​ S​​ trên mặt phẳng​​ ABC​​ là trung điểm​​ H​​ của​​ cạnh​​ BC. Góc giữa đường thẳng​​ SA​​ và mặt phẳng​​ ABC​​ bằng​​ 600.​​ Tính theo​​ a​​ thể tích​​ V​​ của khối chóp​​ S.ABC.

 A.​​ V=a338.​​  B.​​ V=3a338.​​  C.​​ V=a334.​​  D.​​ V=a333.

Câu 28. Cho hình chóp​​ S.ABC​​ có đáy​​ ABC​​ là tam giác vuông tại​​ B; đỉnh​​ S​​ cách đều các điểm​​ A,B,C.​​ Biết​​ AC=2a,BC=a; góc giữa đường thẳng​​ SB​​ và mặt đáy​​ ABC​​ bằng​​ 600. Tính theo​​ a​​ thể tích​​ V​​ của khối chóp​​ S.ABC.

 A.​​ V=a364.​​  B.​​ V=a366.​​  C.​​ V=a32.​​  D.​​ V=a3612.​​ 

Câu 29.​​ Cho hình chóp​​ S.ABCD​​ có đáy​​ ABCD​​ là hình vuông tâm​​ O,​​ BD=1. Hình chiếu vuông góc​​ H​​ của đỉnh​​ S​​ trên mặt phẳng đáy​​ ABCD​​ là trung điểm​​ OD. Đường thẳng​​ SD​​ tạo với mặt đáy một góc bằng​​ 600. Tính thể tích khối chóp​​ S.ABCD.

 A.​​ V=324.​​  B.​​ V=38.​​  C.​​ V=18.​​  D.​​ V=312.​​ 

Câu 30.​​ Cho hình chóp​​ S.ABCD​​ có đáy​​ ABCD​​ là hình thoi cạnh​​ a. Tam giác​​ ABC​​ đều, hình chiếu vuông góc​​ H​​ của đỉnh​​ S​​ trên mặt phẳng​​ ABCD​​ trùng với trọng tâm của tam giác​​ ABC. Đường thẳng​​ SD​​ hợp với mặt phẳng​​ ABCD​​ góc​​ 300. Tính theo​​ a​​ thể tích​​ V​​ của khối chóp​​ S.ABCD.​​ 

 A.​​ V=a333.​​  B.​​ V=a33.​​  C.​​ V=a339.​​  D.​​ V=2a339.​​ 

Câu 31.​​ Cho hình chóp​​ S.ABCD​​ có đáy​​ ABCD​​ là hình thang cân với cạnh đáy​​ AD​​ và​​ BC;​​ AD=2a,AB=BC=CD=a.​​ Cạnh bên​​ SA​​ vuông góc với mặt phẳng​​ ABCD​​ và​​ SD​​ tạo với mặt phẳng​​ ABCD​​ góc​​ 450. Tính thể tích​​ V​​ của khối chóp đã cho.

 A.​​ V=a336.​​  B.​​ V=a332.​​  C.​​ V=3a332.​​  D.​​ V=a33.​​ 

Câu 32.​​ Cho hình chóp​​ S.ABCD​​ có đáy​​ ABCD​​ là hình chữ nhật, mặt bên​​ SAD​​ là tam giác vuông tại​​ S. Hình chiếu vuông góc của​​ S​​ trên mặt đáy là điểm​​ H​​ thuộc cạnh​​ AD​​ sao cho​​ HA=3HD. Biết rằng​​ SA=2a3​​ và​​ SC​​ tạo với đáy một góc bằng​​ 300. Tính theo​​ a​​ thể tích​​ V​​ của khối chóp​​ S.ABCD.

 A.​​ V=86a39.​​  B.​​ V=82a3.​​  C.​​ V=86a3.​​  D.​​ V=86a33.​​ 

Câu 33.​​ Cho hình chóp​​ S.ABCD​​ có đáy​​ ABCD​​ là hình chữ nhật, cạnh bên​​ SA​​ vuông góc với đáy và​​ SA=AB=a. Gọi​​ N​​ là trung điểm​​ SD, đường thẳng​​ AN​​ hợp với đáy​​ ABCD​​ một góc​​ 300. Tính theo​​ a​​ thể tích​​ V​​ của khối chóp​​ S.ABCD.

 A.​​ V=a339.​​  B.​​ V=a333.​​  C.​​ V=a33.​​  D.​​ V=a336.​​ 

Câu 34. (ĐỀ THAM KHẢO 2016 – 2017)​​ Cho hình chóp​​ S.ABCD​​ có đáy​​ ABCD​​ là hình vuông cạnh​​ a,​​ SA​​ vuông góc với mặt đáy,​​ SD​​ tạo với mặt phẳng​​ SAB​​ một góc bằng​​ 300. Tính theo​​ a​​ thể tích​​ V​​ của khối chóp​​ S.ABCD.

 A.​​ V=6a318.​​  B.​​ V=3a3.​​  C.​​ V=6a33.​​  D.​​ V=3a33.

Câu 35.​​ Cho hình chóp​​ S.ABCD​​ có đáy​​ ABCD​​ là hình vuông cạnh bằng​​ 3, tam giác​​ SBC​​ vuông tại​​ S​​ và nằm trong mặt phẳng vuông góc với đáy,​​ đường thẳng​​ SD​​ tạo với mặt phẳng​​ SBC​​ một góc​​ 600. Tính thể tích​​ V​​ của khối chóp​​ S.ABCD.

 A.​​ V=16.​​  B.​​ V=6.​​  C.​​ V=63.​​  D.​​ V=3.​​ 

Câu 36.​​ Cho hình chóp đều​​ S.ABC​​ có cạnh đáy bằng​​ a, góc giữa mặt bên với mặt đáy bằng​​ 600. Tính theo​​ a​​ thể tích​​ V​​ của khối chóp​​ S.ABC.

 A.​​ V=a3324.​​  B.​​ V=a338.​​  C.​​ V=a38.​​  D.​​ V=a3312.​​ 

Câu 37.​​ Cho hình chóp​​ S.ABCD​​ có đáy​​ ABCD​​ là hình vuông cạnh​​ a. Đường thẳng​​ SA​​ vuông góc đáy và mặt bên​​ SCD​​ hợp với đáy một góc bằng​​ 600. Tính theo​​ a​​ thể tích​​ V​​ của khối chóp​​ S.ABCD.

 A.​​ V=a339.​​  B.​​ V=a336.​​  C.​​ V=a33.​​  D.​​ V=a333.​​ 

Câu 38.​​ (ĐỀ CHÍNH THỨC 2016 – 2017)​​ Cho khối chóp​​ S.ABCD​​ có đáy là hình chữ nhật,​​ AB=a,  AD=a3,​​ SA​​ vuông góc với đáy và mặt phẳng​​ SBC​​ tạo với đáy một góc​​ 600. Tính thể tích​​ V​​ của khối chóp​​ S.ABCD.

 A.​​ V=3a3.​​  B.​​ V=3 a33.​​  C.​​ V=a3.​​  D.​​ V=a33.

Câu 39.​​ Cho hình chóp​​ S.ABCD​​ có đáy​​ ABCD​​ là hình vuông cạnh​​ a, cạnh bên​​ SA​​ vuông góc với mặt phẳng đáy, góc giữa mặt phẳng​​ SBD​​ và mặt phẳng​​ ABCD​​ bằng​​ 600. Tính theo​​ a​​ thể tích​​ V​​ của khối chóp​​ S.ABCD.

 A.​​ V=a3612.​​  B.​​ V=a3.​​  C.​​ V=a366. D.​​ V=a362.​​ 

Câu 40.​​ Cho hình chóp​​ S.ABCD​​ có đáy​​ ABCD​​ là hình thoi cạnh​​ a, đường chéo​​ AC=a, tam giác​​ SAB​​ cân tại​​ S​​ và nằm trong mặt phẳng vuông góc với đáy, góc giữa​​ SCD​​ và đáy bằng​​ 450. Tính theo​​ a​​ thể tích​​ V​​ của khối chóp​​ S.ABCD.

 A.​​ V=a34.​​  B.​​ V=3a34.​​  C.​​ V=a32. D.​​ V=a312.​​ 

Câu 41.​​ Cho hình chóp​​ S.ABCD​​ có đáy​​ ABCD​​ là hình thang vuông tại​​ A​​ và​​ D,​​ AD=DC=1,​​ AB=2; cạnh bên​​ SA​​ vuông góc với đáy; mặt phẳng​​ SBC​​ tạo với mặt đáy​​ ABCD​​ một góc​​ 450. Tính thể tích​​ Vcủa khối chóp​​ S.ABCD.

 A.​​ V=2.​​  B.​​ V=322.​​  C.​​ V=22.​​  D.​​ V=26.​​ 

Câu 42.​​ Cho tứ diện​​ ABCD​​ có​​ SΔABC=4cm2,​​ SΔABD=6cm2,​​ AB=3cm. Góc giữa hai mặt phẳng​​ ABC​​ và​​ ABD​​ bằng​​ 60ο. Tính thể tích​​ V​​ của khối tứ diện đã cho.

 A.​​ V=233cm3. B.​​ V=433cm3. C.​​ V=23cm3. D.​​ V=833cm3.

Câu 43. (ĐỀ MINH HỌA 2016 – 2017)​​ Cho tứ diện​​ ABCD​​ có các cạnh​​ AB,AC​​ và​​ AD​​ đôi một vuông góc với nhau;​​ AB=6a, AC=7a​​ và​​ AD=4a.​​ Gọi​​ M,N,P​​ tương ứng là trung điểm các cạnh​​ BC, CD, BD.​​ Tính thể tích​​ V​​ của tứ diện​​ AMNP.​​ 

 A.​​ V=72a3. B.​​ V=14a3. C.​​ V=283a3. D.​​ V=7a3.​​ 

Câu 44.​​ (ĐỀ THỬ NGHIỆM 2016 – 2017)​​ Cho tứ diện​​ ABCD​​ có thể tích bằng​​ 12​​ và​​ G​​ là trọng tâm của tam giác​​ BCD. Tính thể tích​​ V​​ của khối chóp​​ A.GBC.

 A.​​ V=3.​​  B.​​ V=4.​​  C.​​ V=6.​​  D.​​ V=5.

Câu 45.​​ (ĐỀ CHÍNH THỨC 2016 – 2017)​​ Cho khối chóp​​ S.ABCD​​ có đáy​​ ABCD​​ là hình vuông cạnh​​ a,​​ SA​​ vuông góc với đáy và khoảng cách từ​​ A​​ đến mặt phẳng​​ SBC​​ bằng​​ a22. Tính thể tích​​ V​​ của khối chóp đã cho.​​ 

 A.​​ V=a32.​​  B.​​ V=a3.​​  C.​​ V=3 a39.​​  D.​​ V=a33.

Câu 46.​​ Cho hình chóp​​ S.ABC​​ có đáy​​ ABC​​ là tam giác vuông cân ở​​ B,​​ AC=a2,​​ SA=a​​ và vuông góc với đáy​​ ABC. Gọi​​ G​​ là trọng tâm tam giác​​ SBC. Mặt phẳng​​ α​​ qua​​ AG​​ và song song với​​ BC​​ cắt​​ SB,​​ SC​​ lần lượt tại​​ M,​​ N. Tính theo​​ a​​ thể tích​​ V​​ của khối chóp​​ S.AMN.

 A.​​ V=2a327. B.​​ V=2a329.​​  C.​​ V=a39. D.​​ V=a327.​​ 

Câu 47.​​ Cho hình chóp​​ S.ABCD​​ có đáy​​ ABCD​​ là hình vuông cạnh​​ a. Gọi​​ M​​ và​​ N​​ lần lượt là trung điểm của các cạnh​​ AB​​ và​​ AD;​​ H​​ là giao điểm của​​ CN​​ và​​ DM. Biết​​ SH​​ vuông góc với mặt phẳng​​ ABCD​​ và​​ SH=a3. Tính thể tích khối chóp​​ S.CDNM.

 A.​​ V=5a338. B.​​ V=5a3324.​​  C.​​ V=5a38. D.​​ V=5a3312.

Câu 48.​​ Cho hình chóp tứ giác đều​​ S.ABCD​​ có đáy​​ ABCD​​ là hình vuông tâm​​ O, cạnh​​ 2a. Mặt bên tạo với đáy góc​​ 600. Gọi​​ K​​ là hình chiếu vuông góc của​​ O​​ trên​​ SD. Tính theo​​ a​​ thể tích​​ V​​ của khối tứ diện​​ DKAC.

 A.​​ V=2a3315. B.​​ V=4a335.​​  C.​​ V=4a3315. D.​​ V=a33.

Câu 49*.​​ Cho hình chóp​​ S.ABC​​ có​​ ASB^=CSB^=600,ASC^=900​​ và​​ SA=SB=a,​​ SC=3a. Tính thể tích​​ V​​ của khối chóp​​ S.ABC.

 A.​​ V=a363. B.​​ V=a3612. C.​​ V=a3312. D.​​ V=a324.

Câu 50.​​ Cho hình chóp​​ S.ABCD​​ có đáy​​ ABCD​​ là hình vuông cạnh​​ a,​​ SA=SB,​​ SC=SD,​​ SAB⊥SCD​​ và tổng diện tích hai tam giác​​ SAB​​ và​​ SCD​​ bằng​​ 7a210.​​ Tính thể tích​​ V​​ của khối chóp​​ S.ABCD.

 A.​​ V=a35.​​  B.​​ V=4a315.​​  C.​​ V=4a325.​​  D.​​ V=12a325.

C. Đáp án và lời giải

Câu 1.​​ 

 

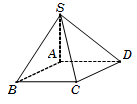
Diện tích hình vuông​​ ABCD​​ là​​ SABCD=a2.

Chiều cao khối chóp là​​ SA=a2.​​ 

Vậy thể tích khối chóp​​ VS.ABCD=13SABCD.SA=a323.

Chọn D. 

Câu 2.​​ Ta chọn​​ SBC​​ làm mặt đáy​​ →​​ chiều cao khối chóp là​​ dA,SBC=3a.

Tam giác​​ SBC​​ vuông cân tại​​ S​​ nên​​ SΔSBC=12SB2=2a2.

Vậy thể tích khối chóp​​ V=13SΔSBC.dA,SBC=2a3.​​ Chọn A.

Câu 3.​​ 

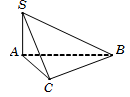
Tam giác​​ ABC, có​​ AB2+AC2=62+82=102=BC2

→tam giác​​ ABC​​ vuông tại​​ A→SΔABC=12AB.AC=24.

Vậy thể tích khối chóp​​ VS.ABC=13SΔABC.SA=32.​​ Chọn C. 

Câu 4.​​ 

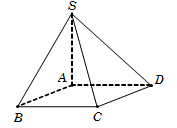
Vì hai mặt bên​​ SAB​​ và​​ SAD​​ cùng vuông góc với​​ ABCD, suy ra​​ SA⊥ABCD. Do đó chiều cao khối chóp là​​ SA=a15.

Diện tích hình chữ nhật​​ ABCD​​ là​​ SABCD=AB.BC=2a2.

Vậy thể tích khối chóp​​ VS.ABCD=13SABCD.SA=2a3153.​​ 

Chọn B. 

Câu 5.​​ 

 

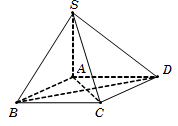
Đường chéo hình vuông​​ AC=a2.

Xét tam giác​​ SAC, ta có​​ SA=SC2-AC2=a3.

Chiều cao khối chóp là​​ SA=a3.​​ 

Diện tích hình vuông​​ ABCD​​ là​​ SABCD=a2.

Vậy thể tích khối chop​​ VS.ABCD=13SABCD.SA=a333.​​ 

Chọn A. 

Câu 6.

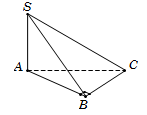
Diện tích tam giác vuông​​ SΔABC=12BA.BC=a22.

Chiều cao khối chóp là​​ SA=2a.​​ 

Vậy thể tích khối chóp​​ VS.ABC=13SABC.SA=a33.

Chọn C. 

Câu 7.​​ 

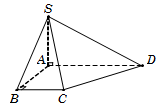
Diện tích hình thang​​ ABCD​​ là​​ 

SABCD=AD+BC2.AB=32.

Chiều cao khối chóp là​​ SA=2.

Vậy thể tích khối chóp​​ VS.ABCD=13SABCD.SA=1.​​ 

Chọn A. 

Câu 8.​​ 

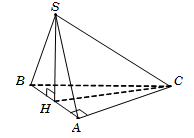
Gọi​​ H​​ là trung điểm của​​ AB, suy ra​​ SH⊥AB.

Do​​ SAB⊥ABC​​ theo giao tuyến​​ AB​​ nên​​ SH⊥ABC.

Tam giác​​ SAB​​ là đều cạnh​​ AB=a​​ nên​​ SH=a32.

Tam giác vuông​​ ABC, có​​ AC=BC2-AB2=a2.

Diện tích tam giác vuông​​ SΔABC=12AB.AC=a222.

Vậy​​ VS.ABC=13SΔABC.SH=a3612.​​ Chọn A. 

Câu 9.

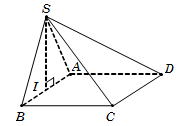
Gọi​​ I​​ là trung điểm của​​ AB. Tam giác​​ SAB​​ cân tại​​ S​​ và có​​ I​​ là trung điểm​​ AB​​ nên​​ SI⊥AB. Do​​ SAB⊥ABCD​​ theo giao tuyến​​ AB​​ nên​​ SI⊥ABCD.

Tam giác vuông​​ SIA, có​​ 

SI=SA2-IA2=SA2-AB22=a152.

Diện tích hình vuông​​ ABCD​​ là​​ SABCD=a2.

Vậy​​ VS.ABCD=13SABCD.SI=a3156.​​ 

Chọn B. 

Câu 10.​​ 

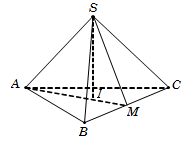
Gọi​​ I​​ là tâm đường tròn ngoại tiếp tam giác​​ ABC.​​ Vì​​ S.ABC​​ là khối chóp đều nên suy ra  SI⊥ABC.

Gọi​​ M​​ là trung điểm của​​ BC  ⇒  AI=23AM=a33.

Tam giác​​ SAI​​ vuông tại​​ I, có​​ 

SI=SA2-SI2=2a2-a332=a333.

Diện tích tam giác​​ ABC​​ là​​ SΔABC=a234. 

Vậy thể tích khối chóp​​ VS.ABCD=13SΔABC.SI=11 a312.​​ 

Chọn B.

Câu 11.​​ 

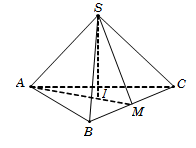
Gọi​​ I​​ là tâm đường tròn ngoại tiếp tam giác​​ ABC.​​ Vì​​ S.ABC​​ là khối chóp đều nên suy ra  SI⊥ABC.

Gọi​​ M​​ là trung điểm của​​ BC  ⇒  AI=23AM=a33.

Tam giác​​ SAI​​ vuông tại​​ I, có ​​ 

SI=SA2-AI2a2162-a332=a2.

Diện tích tam giác​​ ABC​​ là​​ SΔABC=a234. 

Vậy thể tích khối chóp​​ VS.ABC=13SΔABC.SI=a3324​​ 

Chọn C.

 

Câu 12.​​ Xét hình chóp​​ S.ABC​​ có đáy​​ ABC​​ là tam giác đều cạnh​​ 2a⇒  SΔABC=a23.​​ 

Thể tích khối chóp​​ VS.ABC=13SΔABC.h→h=3.VS.ABCSΔABC=3a3a23=a3.​​ Chọn D.

Câu 13.​​ Gọi​​ M​​ là trung điểm​​ AC. Theo giả thiết, ta có​​ SM⊥ABC⇒SM⊥AC.

Tam giác vuông​​ ABC, có​​ AC=AB2=a2.

Tam giác vuông​​ SMA, có​​ 

SM=SA2-AM2=SA2-AC22=a62.

Diện tích tam giác vuông cân​​ ABC​​ là​​ SΔABC=a22.

Vậy​​ VS.ABC=13SΔABC.SM=a3612.​​ Chọn A. 

Câu 14.​​ 

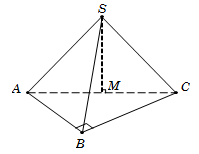
Vì​​ ABC^=60°​​ nên tam giác​​ ABC​​ đều.

Suy ra​​ 

BO=32;BD=2BO=3;HD=34BD=334.

Tam giác vuông​​ SHD, có​​ SH=SD2-HD2=54.

Diện tích hình thoi​​ ABCD​​ là​​ SABCD=2SΔABC=32 . 

Vậy thể tích khối chóp​​ VS.ABCD=13SABCD.SH=1524.​​ Chọn B.

Câu 15.​​ 

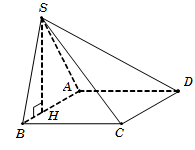
Trong tam giác vuông​​ SAB, ta có​​ 

SA2=AH.AB=23AB.AB=23a2;

SH=SA2-AH2=a23.

Diện tích hình vuông​​ ABCD​​ là​​ SABCD=a2.

Vậy​​ VS.ABCD=13SABCD.SH=a329.​​ Chọn D. 

Câu 16.​​ 

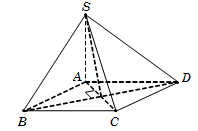
Ta có​​ ΔSAB=ΔSAD→SB=SD.

Hơn nữa, theo giả thiết​​ SBD^=600.

Do đó​​ ΔSBD​​ đều cạnh​​ SB=SD=BD=a2.

Tam giác vuông​​ SAB, ta có​​ SA=SB2-AB2=a.

Diện tích hình vuông​​ ABCD​​ là​​ SABCD=a2.

Vậy​​ VS.ABCD=13SABCD.SA=a33​​ (đvtt).​​ Chọn C. 

Câu 17.​​ 

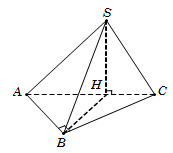
Kẻ​​ SH⊥AC. Do​​ SAC⊥ABC​​ theo giao tuyến​​ AC​​ nên​​ SH⊥ABC.

Trong tam giác vuông​​ SAC, ta có

 SC=AC2-SA2=a3,​​ SH=SA.SCAC=a32.

Tam giác vuông​​ ABC, có​​ BC=AC2-AB2=a3.

Diện tích tam giác​​ ABC​​ là​​ SΔABC=12AB.BC=a232.

Vậy​​ VS.ABC=13SΔABC.SH=a34.​​ Chọn A. 

Câu 18.​​ 

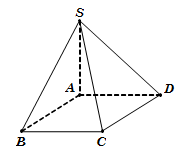
Ta có​​ BC⊥AB​​ (do​​ ABCD​​ là hình vuông). 1

Lại có​​ BC⊥SA​​ (do​​ SA​​ vuông góc với đáy​​ ABCD). 2

Từ​​ 1​​ và​​ 2, suy ra​​ BC⊥SAB⇒BC⊥SB. Do đó tam giác​​ SBC​​ vuông tại​​ B.​​ 

Đặt cạnh hình vuông là​​ x>0.

Tam giác​​ SAB​​ vuông tại​​ A​​ nên

SB=SA2+AB2=a2+x2.

Theo chứng minh trên, ta có tam giác​​ SBC​​ vuông tại​​ B​​ nên​​ 

a222=SΔABC=12SB.BC=12a2+x2.x→x=a.

Diện tích hình vuông​​ ABCD​​ là​​ SABCD=a2.

Vậy​​ VS.ABCD=13SABCD.SA=a33.​​ Chọn C.

Câu 19.​​ Gọi​​ M,N​​ lần lượt là trung điểm​​ AB,AC.​​ Suy ra​​ G=CM∩BN​​ là trọng tâm tam giác​​ ABC.​​ Theo giả thiết, ta có​​ SG⊥ABC.

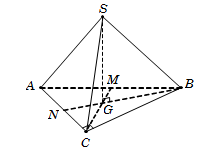
Tam giác​​ ABC​​ vuông cân tại​​ C, suy ra​​ CA=CB=AB2=32​​ 

và​​ CM⊥AB.

Ta có​​ CM=12AB=32, suy ra​​ GM=13CM=12;

BG=BM2+GM2=102;SG=SB2-GB2=1.

Diện tích tam giác​​ ABC​​ là​​ SΔABC=12CA.CB=94.

Vậy​​ VS.ABC=13SΔABC.SG=34.​​ Chọn C. 

Câu 20.​​ Gọi​​ O=AC∩BD.​​ Do​​ S.ABCD​​ là hình chóp đều nên​​ SO⊥ABCD.

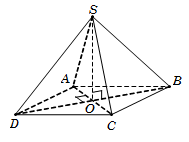
Suy ra​​ OB​​ là hình chiếu của​​ SB​​ trên​​ ABCD.

Khi đó​​ 600=SB,ABCD^=SB,OB^=SBO^.

Tam giác vuông​​ SOB, có​​ SO=OB.tanSBO^=a62.

Diện tích hình vuông​​ ABC​​ là​​ SABCD=AB2=a2.

Vậy​​ VS.ABCD=13SABCD.SO=a366.​​ Chọn A. 

 

Câu 21.​​ Trong tam giác vuông​​ ABC, ta có​​ BC=AC2-AB2=26a.

Vì​​ SA⊥ABCD​​ nên hình chiếu vuông góc của​​ SB​​ trên mặt phẳng​​ ABCD​​ là​​ AB.

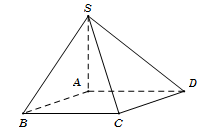
Do đó​​ 600=SB,ABCD^=SB,AB^=SBA^.

Tam giác vuông​​ SAB, có​​ SA=AB.tanSBA^=a3.

Diện tích hình chữ nhật​​ SABCD=AB.BC=26a2.

Vậy​​ VS.ABCD=13SABCD.SA=22a3.​​ Chọn C. 

Câu 22.​​ Do​​ SA⊥ABCD​​ nên ta có​​ 

600=SB,ABC^=SB,AB^=SBA^.

Tam giác vuông​​ SAB, có​​ SA=AB.tanSBA^=a3.

Diện tích tam giác đều​​ ABC​​ là​​ SΔABC=a234.

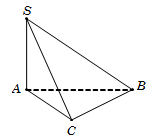
Vậy​​ VS.ABC=13SΔABC.SA=a34.​​ Chọn A. 

Câu 23.​​ Do​​ SA⊥ABCD​​ nên ta có​​ 600=SD,ABCD^=SD,AD^=SDA^.

Tam giác vuông​​ SAD, có​​ SA=AD.tanSDA^=a3.

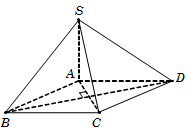
Diện tích hình thoi​​ 

SABCD=2SΔBAD=AB.AD.sinBAD^=a232.

Vậy thể tích khối chop​​ VS.ABCD=13SABCD.SA=a32.​​ 

Chọn C. 

Câu 24.​​ Vì​​ SH⊥ABCD​​ nên hình chiếu vuông góc của​​ SC​​ trên mặt phẳng đáy​​ ABCD​​ là​​ HC.​​ Do đó​​ 300=SC,ABCD^=SC,HC^=SCH^.

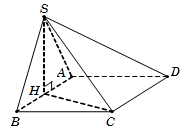
Tam giác vuông​​ BCH, có​​ HC=BC2+BH2=52.

Tam giác vuông​​ SHC, có​​ SH=HC.tanSCH^=156.

Diện tích hình vuông​​ ABCD​​ là​​ SABCD=1.​​ 

Vậy​​ VS.ABCD=13SABCD.SH=1518.​​ Chọn B. 

Câu 25.​​ Gọi​​ O​​ là trung điểm​​ AC, suy ra​​ O​​ là tâm đường tròn ngoại tiếp tam giác​​ ABC.​​ Theo giả thiết đỉnh​​ S​​ cách​​ đều các điểm​​ A,B,C​​ nên hình chiếu của​​ S​​ xuống đáy là điểm​​ O→SO⊥ABCD→hình chiếu vuông góc của​​ SB​​ trên mặt đáy​​ ABCD​​ là​​ OB.​​ 

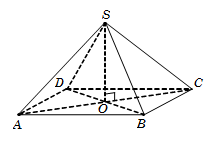
Do đó​​ 600=SB,ABCD^=SB,OB^=SBO^.

Tam giác vuông​​ SOB, có​​ SO=OB.tanSBO^=a3.

Tam giác vuông​​ ABC, có​​ AB=AC2-BC2=a3.

Diện tích hình chữ nhật​​ SABCD=AB.BC=a23.

Vậy​​ VS.ABCD=13SABCD.SO=a3.​​ Chọn D.

Câu 26.​​ Vì​​ SA⊥ABC​​ nên hình chiếu vuông góc của​​ SI​​ trên mặt phẳng​​ ABC​​ là​​ AI. Do đó​​ 60o=SI,ABC^=SI,AI^=SIA^.

Tam giác​​ ABC​​ vuông ​​ tại​​ A, suy ra trung tuyến​​ AI=12BC=a22.

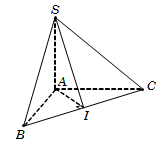
Tam giác vuông​​ SAI, có​​ SA=AI.tanSIA^=a62.

Diện tích tam giác vuông​​ SΔABC=12AB.AC=a22.

Vậy​​ VS.ABC=13SA.SΔABC=a3612.​​ Chọn D.

Câu 27.​​ Vì​​ SH⊥ABC​​ nên hình chiếu vuông góc của​​ SA​​ trên mặt đáy​​ ABC​​ là​​ HA. Do đó​​ 600=SA,ABC^=SA,HA^=SAH^.

Tam giác​​ ABC​​ đều cạnh​​ a​​ nên​​ AH=a32.

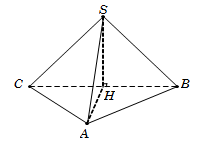
Tam giác vuông​​ SHA, có​​ SH=AH.tanSAH^=3a2.

Diện tích tam giác đều​​ ABC​​ là​​ SΔABC=a234.

Vậy​​ VS.ABC=13SΔABC.SH=a338.​​ Chọn A. 

Câu 28. Gọi​​ H​​ là trung điểm​​ AC. Do tam giác​​ ABC​​ vuông tại​​ B​​ nên​​ H​​ là tâm đường tròn ngoại tiếp tam giác​​ ABC. Đỉnh​​ S​​ cách đều các điểm​​ A,B,C​​ nên hình chiếu của​​ S​​ trên mặt đáy​​ ABC​​ trùng với tâm đường tròn ngoại tiếp tam giác​​ ABC, suy ra​​ SH⊥ABC. Do đó​​ 600=SB,ABC^=SB,BH^=SBH^.

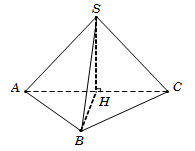
Tam giác vuông​​ SHB, có​​ 

SH=BH.tanSBH^=AC2.tanSBH^=a3.

Tam giác vuông​​ ABC, có​​ AB=AC2-BC2=a3.

Diện tích tam giác vuông​​ SΔABC=12BA.BC=a232.

Vậy​​ VS.ABC=13SΔABC.SH=a32.​​ Chọn C. 

Câu 29.​​ Vì​​ SH⊥ABCD​​ nên hình chiếu vuông góc của​​ SD​​ trên mặt đáy​​ ABCD​​ là​​ HD. Do đó​​ 600=SD,ABCD^=SD,HD^=SDH^.

Tam giác vuông​​ SHD, có​​ 

SH=HD.tanSDH^=BD4.tanSDH^=34.

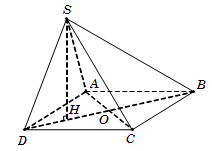
Trong hình vuông​​ ABCD, có​​ AB=BD2=12.

Diện tích hình vuông​​ ABCD​​ là​​ SABCD=AB2=12.

Vậy​​ VS.ABCD=13SABCD.SH=324.​​ Chọn A. 

Câu 30.​​ Gọi​​ O=AC∩BD;​​ M​​ là trung điểm​​ AB. Suy ra​​ H=BO∩CM.

Theo giả thiết​​ SH⊥ABCD​​ nên hình chiếu vuông góc của​​ SD​​ trên mặt đáy​​ ABCD​​ là​​ HD. Do đó​​ 300=SD,ABCD^=SD,HD^=SDH^.

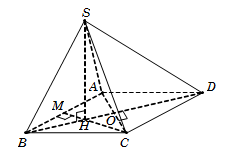
Tam giác​​ ABC​​ và​​ ADC​​ đều cạnh​​ a, suy ra

OD=a32OH=13BO=a36⇒HD=OD+OH=2a33.

Tam giác vuông​​ SHD, có​​ SH=HD.tanSDH^=2a3.

Diện tích hình thoi​​ SABCD=2SΔABC=2.a234=a232.

Vậy​​ VS.ABCD=13SABCD.SH=a339.​​ Chọn C.

 

Câu 31.​​ Ta có​​ 450=SD,ABCD^=SD,AD^=SDA^.

Suy ra tam giác​​ SAD​​ vuông cân tại​​ A​​ nên​​ SA=AD=2a.

Trong​​ hình thang​​ ABCD, kẻ​​ BH⊥AD​​ H∈AD.

Do​​ ABCD​​ là hình thang cân​​ nên​​ AH=AD-BC2=a2.

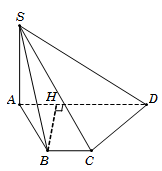
Tam giác​​ AHB,​​ có​​ BH=AB2-AH2=a32.

Diện tích​​ SABCD=12AD+BCBH=3a234.

Vậy​​ VS.ABCD=13SABCD.SA=a332.​​ Chọn B.

Câu 32.​​ Hình chiếu vuông góc của​​ SC​​ trên mặt đáy là​​ HC​​ nên​​ 

 300=SC,ABCD^=SC,HC^=SCH^.

Tam giác vuông​​ SAD, có​​ SA2=AH.AD

 ⇔12a2=34AD.AD=34AD2.

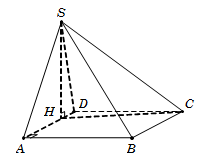
Suy ra​​ AD=4a,​​ HA=3a,​​ HD=a,​​ SH=HA.HD=a3,

HC=SH.cotSCH^=3a,CD=HC2-HD2=2a2.

Diện tích hình chữ nhật​​ ABCD​​ là​​ SABCD=AD.CD=82a2.

Vậy ​​ thể tích khối chop​​ VS.ABCD=13SABCD.SH=86a33.​​ Chọn D.

Câu 33.​​ Tam giác​​ SAD​​ vuông tại​​ A, có​​ AN​​ là trung tuyến nên​​ AN=12SD.

Gọi​​ M​​ là trung điểm​​ AD, suy ra​​ MN∥SA​​ nên​​ MN⊥ABCD.

Do đó​​ 300=AN,ABCD^=AN,AM^=NAM^.

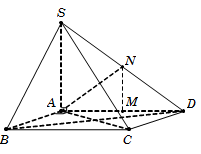
Tam giác vuông​​ NMA, có​​ AM=AN.cosNAM^=SD34.

Tam giác​​ SAD, có​​ SD2=SA2+AD2⇔SD2=a2+SD322​​ .

Suy ra​​ SD=2a​​ nên​​ AD=a3.​​ 

Diện tích hình chữ nhật​​ SABCD=AB.AD=a23.

Vậy​​ VS.ABCD=13SABCD.SA=a333.​​ Chọn B.

Câu 34.​​ ABCD​​ là hình vuông suy ra​​ AB⊥AD. (1)​​ 

Vì​​ SA⊥ABCD →SA⊥AD.​​   2​​ 

Từ​​ 1​​ và​​ 2, suy ra​​ AD⊥SAB.

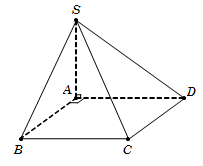
Khi đó​​ SA​​ là hình chiếu của​​ SD​​ trên mặt phẳng​​ SAB.

Do đó​​ 300=  SD;SAB^=SD;SA^=DSA^.

Tam giác​​ SAD​​ vuông tại​​ A, có​​ SA=ADtanDSA^=a3.

Vậy thể tích khối chóp​​ VS.ABCD=13SABCD.SA=a333.​​ Chọn D.

Câu 35.​​ Kẻ​​ SH⊥BC. Vì​​ SBC⊥ABCD​​ theo giao tuyến​​ BC​​ nên​​ SH⊥ABCD.

Ta có​​ DC⊥BCDC⊥SH⇒DC⊥SBC. Do đó​​ 600=SD,SBC^=SD,SC^=DSC^.

Từ​​ DC⊥SBC→DC⊥SC.

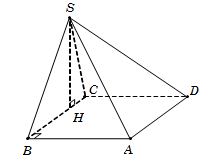
Tam giác vuông​​ SCD,​​ có​​ SC=DCtanDSC^=1.

Tam giác vuông​​ SBC, có​​ 

SH=SB.SCBC=BC2-SC2.SCBC=63.

Diện tích hình vuông​​ ABCD​​ là​​ SABCD=3.

Vậy​​ VS.ABCD=13SABCD.SH=63.​​ Chọn C. 

 

Câu 36.​​ Gọi​​ E,F​​ lần lượt là trung điểm​​ BC,BA​​ vàO=AE∩CF.

Do​​ S.ABC​​ là hình chóp đều nên​​ SO⊥ABC.

Khi đó​​ 600=SBC,ABC^=SE,OE^=SEO^.

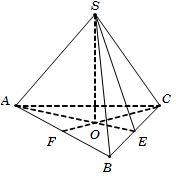
Tam giác vuông​​ SOE, có​​ 

SO=OE.tanSEO^=AE3.tan600=a36.3=a2.

Diện tích tam giác đều​​ ABC​​ là​​ SΔABC=a234.

Vậy​​ VS.ABC=13SΔABC.SO=a3324.​​ Chọn A.

 

Câu 37.​​ Ta có​​ SA⊥ABCD⇒SA⊥CDnên cóCD⊥ADCD⊥SA⇒CD⊥SAD⇒CD⊥SD.

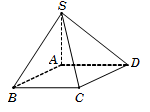
Do​​ SCD∩ABCD=CDSD⊥CD;AD⊥CD, suy ra​​ 600=SCD,ABCD^=SD,AD^=SDA^.

Tam giác vuông​​ SAD, có​​ SA=AD.tanSDA^=a3.

Diện tích hình vuông​​ ABCD​​ là​​ SABCD=AB2=a2.

Vậy thể tích khối chóp​​ VS.ABCD=13SABCD.SA=a333.

Chọn D. 

Câu 38.​​ Ta có​​ SA⊥ABCD⇒SA⊥BCnên cóBC⊥ABBC⊥SA⇒BC⊥SAB⇒BC⊥SB.

 

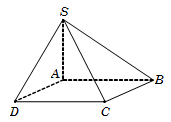
Do​​ SBC∩ABCD=BCSB⊥BC;AB⊥BC, suy ra​​ 600=SBC,ABCD^=SB,AB^=SBA^.

Tam giác vuông​​ SAB, có​​ SA=AB.tanSBA^=a3.

Diện tích hình chữ nhật​​ ABCD​​ là​​ 

SABCD=AB.AD=a23.

Vậy thể tích khối chóp​​ VS.ABCD=13SABCD.SA=a3.

Chọn C. 

Câu 39.​​ Vì​​ SA⊥ABCD⇒SA⊥BD. 1

Gọi​​ O=AC∩BD, suy ra​​ BD⊥AO. 2

Từ​​ 1​​ và​​ 2, suy ra​​ BD⊥SAO⇒BD⊥SO.

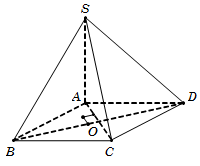
Do​​ SBD∩ABCD=BDSO⊥BD,AO⊥BD, suy ra​​ 

 600=SBD,ABCD^=SO,AO^=SOA^.

Tam giác vuông​​ SAO, ta có​​ SA=AO.tanSOA^=a62.

Diện tích hình vuông​​ ABCD​​ là​​ SABCD=a2.

Vậy​​ VS.ABCD=13SABCD.SA=a366.​​ Chọn C.

Câu 40.​​ Gọi​​ H​​ là trung điểm​​ AB, suy ra​​ SH⊥AB.​​ 

Mà​​ SAB⊥ABCD​​ theo giao tuyến​​ AB​​ nên​​ SH⊥ABCD.

Tam giác​​ ABC​​ đều cạnh​​ a​​ nên

​​ CH⊥AB→CH⊥CDCH=AB32=a32.

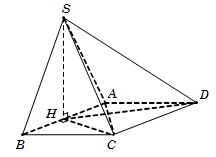
Ta có​​ SCD∩ABCD=CDSC⊂SCD,SC⊥CDHC⊂ABCD,HC⊥CD​​ suy ra​​ 

450=SCD,ABCD^=SC,HC^=SCH^.

Tam giác vuông​​ SHC, có​​ SH=HC.tanSCH^=a32.

Diện tích hình thoi​​ ABCD​​ là​​ SABCD=2SΔADC=a232.

Vậy thể tích khối chóp​​ VS.ABCD=13SABCD.SH=a34.​​ Chọn A.

Câu 41.​​ Gọi​​ I​​ là trung điểm​​ AB, suy ra​​ CI=AD=1=12AB.

Do đó tam giác​​ ABC​​ vuông tại​​ C. Suy ra​​ BC⊥AC​​ nên​​ 

450=SBC,ABCD^=SC,AC^=SCA^.

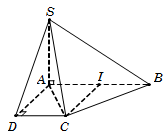
Ta có​​ AC=AD2+DC2=2.

Tam giác vuông​​ SAC, có​​ SA=AC.tanSCA^=2.

Diện tích hình thang​​ SABCD=AB+DCAD2=32.

Vậy thể tích khối chóp​​ VS.ABCD=13SABCD.SA=22.

Chọn C.

Câu 42.​​ 

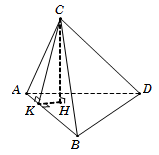
Kẻ​​ CK⊥AB. Ta có​​ SΔABC=12AB.CK→CK=83cm.​​ 

Gọi​​ H​​ là chân đường cao của hình chóp hạ từ đỉnh​​ C.​​ 

Xét tam giác vuông​​ CHK, ta có​​ 

CH=CK.sinCKH^=CK.sinABC,ABD^=433.

Vậy thể tích khối tứ diện​​ V=13SΔABD.CH=833cm3.​​ Chọn D.

Câu 43.​​ Do​​ AB,AC​​ và​​ AD​​ đôi một vuông góc với nhau nên

VABCD=16AB.AC.AD=16.6a.7a.4a=28a3.

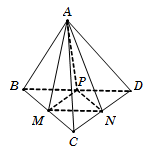
Dễ thấy​​ SΔMNP=14SΔBCD.

Suy ra​​ VAMNP=14VABCD=7a3.​​ Chọn D.

Câu 44.​​ Vì​​ G​​ là trọng tâm của tam giác​​ BCD​​ nên​​ SΔGBC=13SΔDBC.

Suy ra​​ VA.GBC=13VABCD=13.12=4.​​ Chọn B.

Câu 45.​​ Gọi​​ H​​ là hình chiếu của​​ A​​ trên​​ SB⇒AH⊥SB.

Ta có​​ SA⊥ABCD⇒SA⊥BCAB⊥BC⇒BC⊥SAB⇒AH⊥BC.

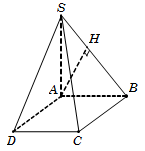
Suy ra​​ AH⊥SBC⇒dA,SBC=AH=a22.

Tam giác​​ SAB​​ vuông tại​​ A, có​​ 1AH2=1SA2+1AB2⇒SA=a.

Vậy​​ V=13.SA.SABCD=a33.​​ Chọn D. 

Câu 46.​​ Từ giả thiết suy ra​​ AB=BC=a.

Diện tích tam giác​​ SΔABC=12AB.BC=a22.​​ 

Do đó​​ VS.ABC=13SΔABC.SA=a36.

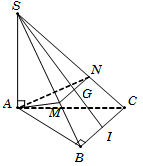
Gọi​​ I​​ là trung điểm​​ BC.​​ 

Do​​ G​​ là trọng tâm​​ ΔSBC​​ nên​​ SGSI=23.

Vì​​ BC∥α→BC​​ song song với giao tuyến​​ MN

→ΔAMN∽ΔABC​​ theo tỉ số​​ 23→SΔAMN=49SΔSBC.​​ 

Vậy thể tích khối chóp​​ VS.AMN=49.VS.ABC=2a327.

Chọn A.

Nhận xét.​​ 

1) bạn đọc có thể tham khảo cách giải khác bằng tỉ số thể tích​​ 

2) Hai tam giác đồng dạng theo tỉ số​​ k​​ thì tỉ số thể tích bằng​​ k2.​​ 

 

Câu 47.​​ 

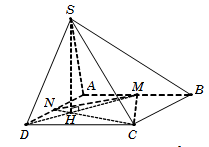
Theo giả thiết, ta có​​ SH=a3.

Diện tích tứ giác​​ SCDNM=SABCD-SΔAMN-SΔBMC

=AB2-12AM.AN-12BM.BC=a2-a28-a24=5a28.

Vậy​​ VS.CDNM=13SCDNM.SH=5a3324.​​ Chọn B. 

Câu 48.​​ Gọi​​ M​​ là trung điểm​​ CD, suy ra​​ OM⊥CD​​ nên​​ 

 600=SCD,ABCD^=SM,OM^=SMO^.

Tam giác vuông​​ SOM, có​​ SO=OM.tanSMO^=a3.

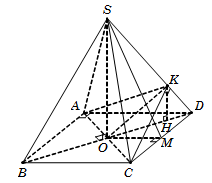
Kẻ​​ KH⊥OD⇒KH∥SO​​ nên​​ KH⊥ABCD.

Tam giác vuông​​ SOD, ta có​​ KHSO=DKDS=DO2DS2

=OD2SO2+OD2=25→KH=25SO=2a35.

Diện tích tam giác​​ SΔADC=12AD.DC=2a2.

Vậy​​ VDKAC=13SΔADC.KH=4a3315.​​ Chọn C.

Câu 49*.​​ Gọi​​ M​​ là trung điểm của​​ AB⇒SM⊥AB.​​ (1)​​ 

Ta có​​ SA=SBASB^=600⇒ΔSAB​​ đều→AB=aSM=a32.

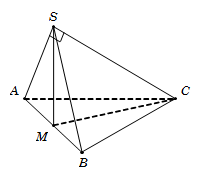
Tam giác​​ SAC, có​​ AC=SA2+SC2=a10.

Tam giác​​ SBC, có​​ BC=SB2+SC2-2SB.SC.cosBSC^=a7.

Tam giác​​ ABC, có​​ cosBAC^=AB2+AC2-BC22AB.AC=105.​​ 

→CM=AM2+AC2-2AM.AC.cosBAC^=a332.​​ 

Ta có​​ SM2+MC2=SC2=9a2→ΔSMC​​ vuông tại​​ M→SM⊥MC.​​  2

Từ​​ 1​​ và​​ 2, ta có​​ SM⊥ABC.

Diện tích tam giác​​ SΔABC=12AB.AC.sinBAC^=a262.

Vậy thể tích khối chop​​ VSABC=13SΔABC.SM=a324.​​ Chọn D.

Cách 2.​​ (Dùng phương pháp tỉ số thể tích).

Trên cạnh​​ SC​​ lấy điểm​​ D​​ sao cho​​ SD=a.

Dễ dàng suy ra

​​ AB=CD=a,AD=a2SA=SD=a,AD=a2→ΔABDvuongcanΔSADvuongcan.

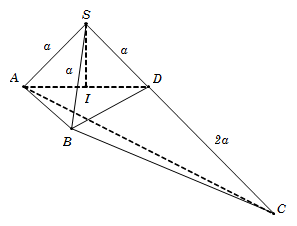
Lại có​​ SA=SB=SD=a​​ nên hình chiếu vuông góc của​​ S​​ trên mặt phẳng​​ ABD​​ là trung điểm​​ I​​ của​​ AD.

Ta tính được​​ SI=a22​​ và​​ SΔABD=12a2.

Suy ra​​ VS.ABD=13SΔABD.SI=a3212.

Ta có​​ VS.ABDVS.ABC=SDSC=13

→VS.ABC=3VS.ABD=a324.​​ 

 

 

Cách 3.​​ Phương pháp trắc nghiệm.​​ ''​​ Cho hình chóp​​ S.ABC​​ có​​ ASB^=α,BSC^=β,CSA^=γ​​ và​​ SA=a,​​ SB=b,​​ SC=c.''​​ Khi đó ta có:​​ 

VS.ABC=abc61-cos2α-cos2β-cos2γ-2cosαcosβcosγ.

Áp dụng công thức, ta được​​ VS.ABC=a324.​​ 

 

Câu 50.​​ Gọi​​ M,  N​​ lần lượt là trung điểm của​​ AB​​ và​​ CD.

 

Tam giác​​ SAB​​ cân tại​​ S​​ suy ra​​ SM⊥AB⇒SM⊥d,​​ với​​ d=SAB∩SCD.

Vì​​ SAB⊥SCD​​ suy ra​​ SM⊥SCD⇒SM⊥SN​​ và​​ SMN⊥ABCD.

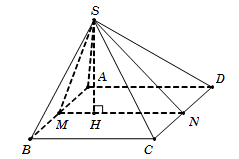
Kẻ​​ SH⊥MN→SH⊥ABCD.

Ta có​​ SΔSAB+SΔSCD=7a210⇔12AB.SM+12CD.SN=7a210→SM+SN=7a5.

Tam giác​​ SMN​​ vuông tại​​ S​​ nên​​ SM2+SN2=MN2=a2.

Giải hệ​​ SM+SN=7a5SM2+SN2=a2⇔SM=3a5&SN=4a5→SH=SM.SNMN=12a25.

Vậy thể tích khối chóp​​ VS.ABCD=13.SABCD.SH=4a325.​​ Chọn C.