I. KHỐI LĂNG TRỤ VÀ KHỐI CHÓP
Khối lăng trụ là phần không gian được giới hạn bởi một hình lăng trụ kể cả hình lăng trụ ấy.
Khối chóp là phần không gian được giới hạn bởi một hình chóp kể cả hình chóp ấy.
Khối chóp cụt là phần không gian được giới hạn bởi một hình chóp cụt kể cả hình chóp cụt ấy.
II. KHÁI NIỆM VỀ HÌNH ĐA DIỆN VÀ KHỐI ĐA DIỆN
1. Khái niệm về hình đa diện
Hình đa diện là hình được tạo bởi một số hữu hạn các đa giác thỏa mãn hai tính chất:
• Hai đa giác phân biệt chỉ có thể hoặc không có điểm chung, hoặc chỉ có một đỉnh chung, hoặc chỉ có một cạnh chung.
• Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác.
Mỗi đa giác như trên được gọi là một mặt của hình đa diện.
Các đỉnh, các cạnh của đa giác ấy theo thứ tự gọi là các đỉnh, các cạnh của hình đa diện.
2. Khái niệm về khối đa diện
• Khối đa diện là phần không gian được giới hạn bởi một hình đa diện, kể cả hình đa diện đó.
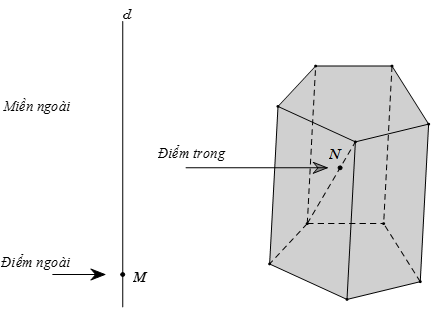
• Những điểm không thuộc khối đa diện được gọi là điểm ngoài của khối đa diện. Tập hợp các điểm ngoài được gọi là miền ngoài của khối đa diện. Những điểm thuộc khối đa diện nhưng không thuộc hình đa diện ứng với đa diện ấy được gọi là điểm trong của khối đa diện. Tập hợp các điểm trong được gọi là miền trong của khối đa diện.
• Mỗi khối đa diện được xác định bởi một hình đa diện ứng với nó. Ta cũng gọi đỉnh, cạnh, mặt, điểm trong, điểm ngoài… của một khối đa diện theo thứ tự là đỉnh, cạnh, mặt, điểm trong, điểm ngoài… của hình đa diện tương ứng.
Ví dụ
- Các hình dưới đây là những khối đa diện:
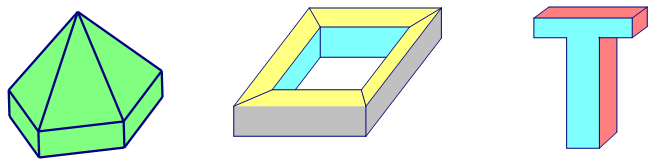
- Các hình dưới đây không phải là những khối đa diện:
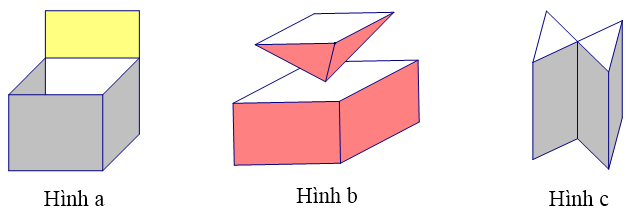
Giải thích: Hình a không phải là hình đa diện vì tồn tại cạnh không phải là cạnh chung của 2 mặt; Hình b không phải là hình đa diện vì có một điểm đặc biệt trong hình, điểm đó không phải là đỉnh chung của 2 đa giác; Hình c không phải là hình đa diện vì tồn tại một cạnh là cạnh chung của bốn đa giác.
III . HAI ĐA DIỆN BẰNG NHAU
1. Phép dời hình trong không gian
• Trong không gian, quy tắc đặt tương ứng mỗi điểm M với điểm M' xác định duy nhất được gọi là một phép biến hình trong không gian.
• Phép biến hình trong không gian được gọi là phép dời hình nếu nó bảo toàn khoảng cách giữa hai điểm tùy ý.
a) Phép tịnh tiến theo vectơ v→, là phép biến hình biến mỗi điểm M thành điểm M' sao cho MM'→ = v→. Kí hiệu là Tv→ .
b) Phép đối xứng qua mặt phẳng (P) là phép biến hình biến mỗi điểm thuộc (P) thành chính nó, biến mỗi điểm M không thuộc (P) thành điểm M' sao cho (P) là mặt phẳng trung trực của MM'.
Nếu phép đối xứng qua mặt phẳng (P) biến hình (H) thành chính nó thì (P) được gọi là mặt phẳng đối xứng của (H).
c) Phép đối xứng tâm O là phép biến hình biến điểm O thành chính nó, biến mỗi điểm M khác O thành điểm M' sao cho O là trung điểm của MM'.
Nếu phép đối xứng tâm O biến hình (H) thành chính nó thì O được gọi là tâm đối xứng của (H).
d) Phép đối xứng qua đường thẳng Δ là là phép biến hình biến mọi điểm thuộc đường thẳng Δ thành chính nó, biến mỗi điểm M không thuộc Δ thành điểm M' sao cho Δ là đường trung trực của MM'.
Nếu phép đối xứng qua đường thẳng Δ biến hình (H) thành chính nó thì Δ được gọi là trục đối xứng của (H).
Nhận xét
• Thực hiện liên tiếp các phép dời hình sẽ được một phép dời hình.
• Phép dời hình biến đa diện (H) thành đa diện (H'), biến đỉnh, cạnh, mặt của (H) thành đỉnh, cạnh, mặt tương ứng của (H').
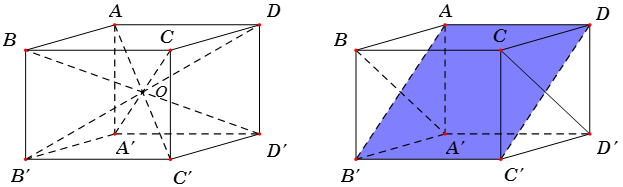
Ví dụ: Cho hình lập phương ABCD.A'B'C'D'. Khi đó:
- Các hình chóp A.A'B'C'D' và C'.ABCD bằng nhau (vì qua phép đối xứng tâm O hình chóp A.A'B'C'D' biến thành hình chóp C'.ABCD).
- Các hình lăng trụ ABC.A'B'C' và AA'D'.BB'C' bằng nhau (vì qua phép đối xứng qua mặt phẳng (AB'C'D) thì hình lăng trụ ABC.A'B'C' biến thành hình lăng trụ AA'D'.BB'C').
2. Hai hình bằng nhau
Hai hình được gọi là nếu có một phép dời hình biến hình này thành hình kia.
Đặc biệt, hai đa diện được gọi là bằng nhau nếu có một phép dời hình biến đa diện này đa diện kia.
IV. PHÂN CHIA VÀ LẮP GHÉP CÁC KHỐI ĐA DIỆN
Nếu khối đa diện (H) là hợp của hai khối đa diện (H1) và (H2) sao cho (H1) và (H2) không có chung điểm trong nào thì ta nói có thể phân chia được khối đa diện (H) thành hai khối đa diện (H1) và (H2). Khi đó ta cũng nói có thể ghép hai khối đa diện (H1) và (H2) để được khối đa diện (H.
Ví dụ: 1 Với khối chóp tứ giác S.ABCD, xét hai khối chóp tam giác S.ABC và S.ACD. Ta thấy rằng:
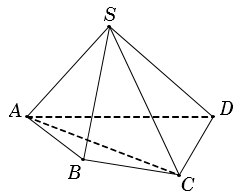
- Hai khối chóp S.ABC và S.ACD không có điểm trong chung (tức là không tồn tại điểm trong của khối chóp này là điểm trong của khối chóp kia và ngược lại).
- Hợp của hai khối chóp S.ABC và S.ACD chính là khối chóp S.ABCD
Vậy khối chóp S.ABCD được phân chia thành hai khối chóp S.ABC và S.ACD hay hai khối chóp S.ABC và S.ACD được ghép lại thành khối chóp S.ABCD
Ví dụ 2. Cắt khối lăng trụ ABC.A'B'C' bởi mặt phẳng (A'BC). Khi đó, khối lăng trụ được phân chia thành hai khối đa diện A'ABC và A'BCC'B'.
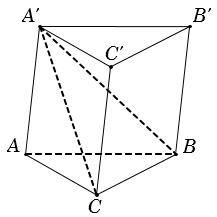
Nếu ta cắt khối chóp A'BCC'B' bởi mặt phẳng (A'B'C) thì ta chia khối chóp A'BCC'B' thành hai khối chóp A'BCB' và A'CC'B'.
Vậy khối lăng trụ ABC.A'B'C' được chia thành ba khối tứ diện là A'ABC, A'BCB' và A'CC'B'.
MỘT SỐ KẾT QUẢ QUAN TRỌNG
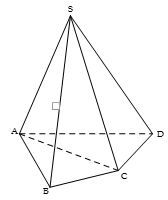
Kết quả 1: Một khối đa diện bất kì có ít nhất 4 mặt.
Kết quả 2: Mỗi hình đa diện có ít nhất 4 đỉnh.
Kết quả 3: Mỗi hình đa diện có ít nhất 6 cạnh.
Kết quả 4: Mỗi đỉnh của một hình đa diện là đỉnh chung của ít nhất 3 cạnh.
Kết quả 5: Không tồn tại hình đa diện có 7 cạnh.
Kết quả 6: Cho (H) là đa diện mà các mặt của nó là những đa giác có p cạnh. Nếu số mặt của (H) là lẻ thì p phải là số chẵn.
Chứng minh: Gọi M là số các mặt của khối đa diện (H). Vì mỗi mặt của (H) có p cạnh nên M mặt sẽ có p.M cạnh. Nhưng do mỗi cạnh là cạnh chung của đúng hai đa giác nên số cạnh của (H) bằng C = (pM)/2. Vì M lẻ nên p phải là số chẵn.
Kết quả 7: (Suy ra từ chứng minh kết quả 6): Cho (H) là đa diện có M mặt, mà các mặt của nó là những đa giác có p cạnh. Khi đó số cạnh của (H) là C = (pM)/2.
Kết quả 8: Mỗi khối đa diện có các mặt là các tam giác thì tổng số các mặt của nó phải là một số chẵn.
Chứng minh: Gọi số cạnh và số mặt của khối đa diện lần lượt là C và M
Vì mỗi mặt có ba cạnh và mỗi cạnh là cạnh chung của đúng hai mặt nên ta có số cạnh của đa diện là 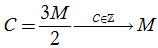
Kết quả 9: Mỗi khối đa diện bất kì luôn có thể được phân chia được thành những khối tứ diện.
Kết quả 10: Nếu khối đa diện có mỗi đỉnh là đỉnh chung của ba cạnh thì số đỉnh phải là số chẵn. (Tổng quát: Một đa diện mà mỗi đỉnh của nó đều là đỉnh chung của một số lẻ mặt thì tổng số đỉnh là một số chẵn)
B.Bài tập trắc nghiệm
Câu 1. Cho các hình sau:
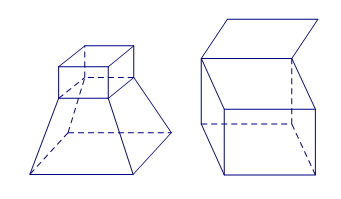
Hình 1 Hình 2
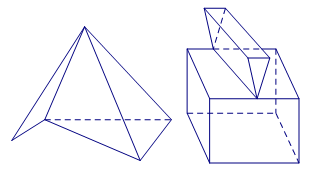
Hình 3 Hình 4
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình đa diện là:
A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4.
Chọn A.
Câu 2. Cho các hình sau:
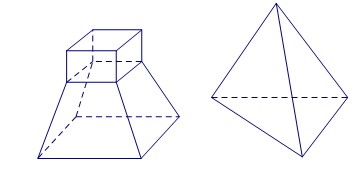
Hình 1 Hình 2
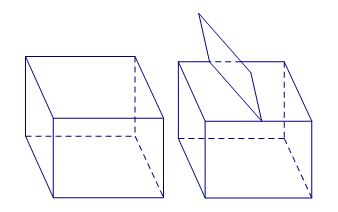
Hình 3 Hình 4
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình không phải đa diện là:
A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4.
Chọn D.
Câu 3. Cho các hình sau:

Hình 1 Hình 2
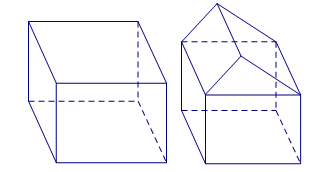
Hình 3 Hình 4
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), số hình đa diện là:
A. 1. B. 2. C. 3. D. 4.
Các hình đa diện là: Hình 1; Hình 3; Hình 4. Chọn C.
Câu 4. Vật thể nào trong các vật thể sau không phải là khối đa diện?
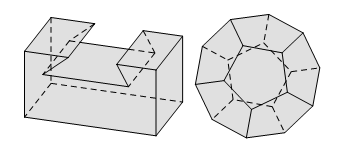
A. B.

C. D.
Chọn C. Vì hình C vi phạm tính chất Mỗi cạnh của miền đa giác nào cũng là cạnh chung của đúng hai miền đa giác.
Câu 5. (ĐỀ THAM KHẢO 2016 – 2017) Hình đa diện trong hình vẽ bên có bao nhiêu mặt ?
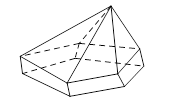
A. B.
C. D.
Chọn C.
Câu 6. Hình đa diện trong hình vẽ bên có bao nhiêu mặt ?
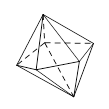
A. B.
C. D.
Chọn B.
Câu 7. Hình đa diện trong hình vẽ bên có bao nhiêu mặt ?
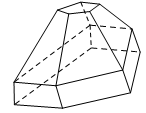
A. B.
C. D.
Chọn B.
Câu 8. Khối đa diện nào sau đây có số mặt nhỏ nhất?
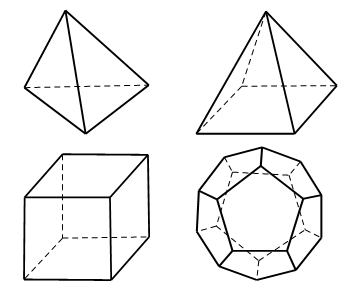
A. Khối tứ diện đều. B. Khối chóp tứ giác.
C. Khối lập phương. D. Khối 12 mặt đều.
Chọn A.
Câu 9. Hình đa diện trong hình vẽ bên có bao nhiêu cạnh?
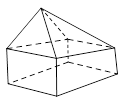
A. B.
C. D.
Chọn D
Câu 10. Cho một hình đa diện. Trong các khẳng định sau, khẳng định nào sai?
A. Mỗi đỉnh là đỉnh chung của ít nhất ba cạnh.
B. Mỗi mặt có ít nhất ba cạnh.
C. Mỗi cạnh là cạnh chung của ít nhất ba mặt.
D. Mỗi đỉnh là đỉnh chung của ít nhất ba mặt.
Ta thấy các đáp án A, B, D đều đúng dựa vào khái niệm hình đa diện.
Chọn C.
Câu 11. Gọi Đ là số các đỉnh, M là số các mặt, C là số các cạnh của một hình đa diện bất kỳ. mệnh đề nào sau đây là đúng?
A. Đ>4,M>4,C>6. B. Đ>5,M>5,C>7.
C. Đ≥4,M≥4,C≥6. D. Đ≥5,M≥5,C≥7.
Xét hình đa diện là hình tứ diện thì kết quả về quan hệ số đỉnh và số mặt thỏa mãn đáp án C. Chọn C.
Câu 12. Một hình đa diện có các mặt là những tam giác. Gọi là tổng số mặt và là tổng số cạnh của đa diện đó. Mệnh đề nào sau đây đúng.
A. 3C=2M. B. C=M+2. C. M≥C. D. 3M=2C.
Vì mỗi mặt là những tam giác nên có tổng số cạnh là Mỗi cạnh là cạnh chung của đúng hai mặt nên ta có hệ thức Chọn D.
Câu 13. (ĐỀ THỬ NGHIỆM 2016 – 2017) Hình đa diện nào dưới đây không có tâm đối xứng?
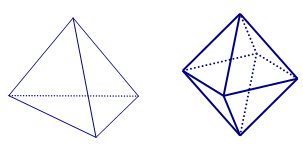
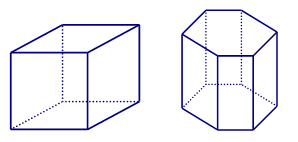
A. Tứ diện đều. B. Bát diện đều. C. Hình lập phương. D. Lăng trụ lục giác đều.
Chọn A.
Câu 14. Gọi n1,n2,n3 lần lượt là số trục đối xứng của khối tứ diện đều, khối chóp tứ giác đều và khối lập phương. Mệnh đề nào sau đây là đúng?
A. n1=0,n2=0,n3=6. B. n1=0,n2=1,n3=9.
C. n1=3,n2=1,n3=9. D. n1=0,n2=1,n3=3.
Khối tứ diện đều có 3 trục đối xứng (đi qua trung điểm của các cặp cạnh đối diện). Khối chóp tứ giác đều có 1 trục đối xứng (đi qua đỉnh và tâm của mặt tứ giác). Khối lập phương có 9 trục đối xứng (Loại 1: đi qua tâm của các mặt đối diện ; Loại 2: đi qua trung điểm các cặp cạnh đối diện). Chọn C.
Câu 15. Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng?
\A. 4 mặt phẳng. B. 1 mặt phẳng.
C. 2 mặt phẳng. D. 3 mặt phẳng.
Hình chóp tứ giác đều có 4 mặt phẳng đối xứng bao gồm:
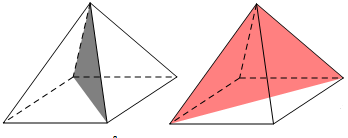

2 mặt phẳng đi qua đỉnh hình chóp và chứa đường trung bình của đáy.
2 mặt phẳng đi qua đỉnh hình chóp và chứa đường chéo của đáy.
Chọn A.
Câu 16. Số mặt phẳng đối xứng của hình tứ diện đều là:
A. 4 mặt phẳng. B. 6 mặt phẳng.
C. 8 mặt phẳng. D. 10 mặt phẳng.
Các mặt phẳng đối xứng của hình tứ diện đều là các mặt phẳng chứa một cạnh và qua trung điểm cạnh đối diện.
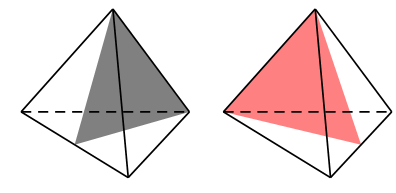
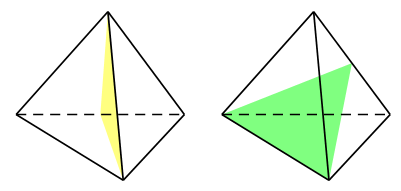
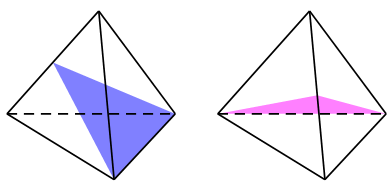
Vậy hình tứ diện đều có 6 mặt phẳng đối xứng. Chọn B.
Câu 17. (ĐỀ CHÍNH THỨC 2016 – 2017) Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng ?
A. 4 mặt phẳng. B. 1 mặt phẳng.
C. 2 mặt phẳng. D. 3 mặt phẳng.
Hình lăng trụ tam giác đều có mặt phẳng đối xứng (hình vẽ bên dưới).
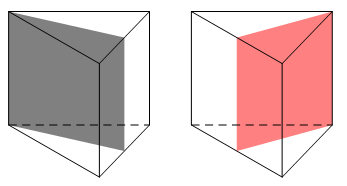
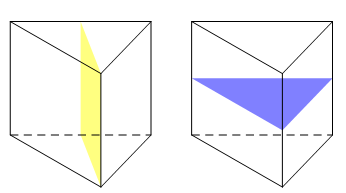
Chọn A.
Câu 18. Hình hộp chữ nhật có ba kích thước đôi một khác nhau có bao nhiêu mặt phẳng đối xứng?
A. mặt phẳng. B. mặt phẳng.
C. mặt phẳng. D. mặt phẳng.
Hình hộp chữ nhật (không là hình lập phương) có các mặt phẳng đối xứng là các mặt các mặt phẳng trung trực của các cặp cạnh đối.
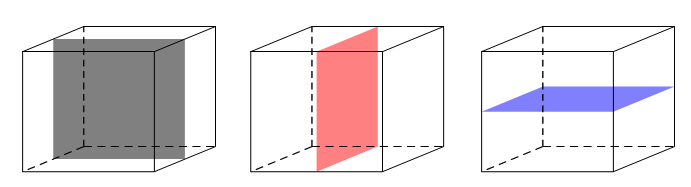
Chọn D.
Hình hộp chữ nhật (không là hình lập phương) có các mặt phẳng đối xứng là các mặt các mặt phẳng trung trực của các cặp cạnh đối.
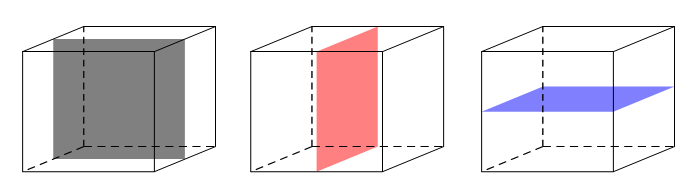
Chọn D.
Câu 19. Một hình hộp đứng có đáy là hình thoi (không phải là hình vuông) có bao nhiêu mặt phẳng đối xứng?
A. mặt phẳng. B. mặt phẳng.
C. mặt phẳng. D. mặt phẳng.
Hình hộp đứng có đáy là hình thoi (không phải là hình chữ nhật) có 3 mặt phẳng đối xứng bao gồm:
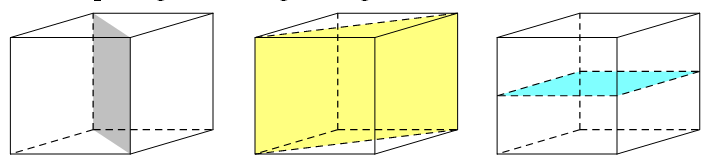
2 mặt phẳng chứa đường chéo của đáy và vuông góc với đáy.
Một mặt phẳng là mặt phẳng trung trực của cạnh bên.
Chọn D.
Câu 20. Hình lập phương có tất cả bao nhiêu mặt phẳng đối xứng?
A. mặt phẳng. B. mặt phẳng.
C. mặt phẳng. D. mặt phẳng.
Có 9 mặt đối xứng (như hình vẽ sau). Chọn B.
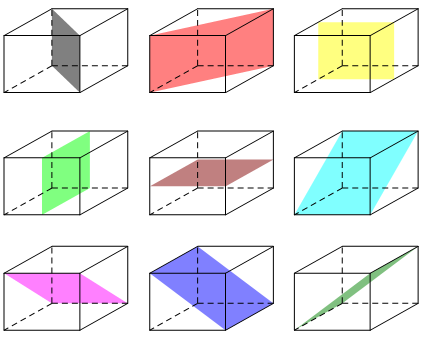
Câu 21. Số mặt phẳng đối xứng của hình bát diện đều là:
A. mặt phẳng. B. mặt phẳng.
C. mặt phẳng. D. mặt phẳng.
Gọi bát diện đều . Có 9 mặt phẳng đối xứng, bao gồm: 3 mặt phẳng , , và 6 mặt phẳng mà mỗi mặt phẳng là mặt phẳng trung trực của hai cạnh song song (chẳng hạn và ).
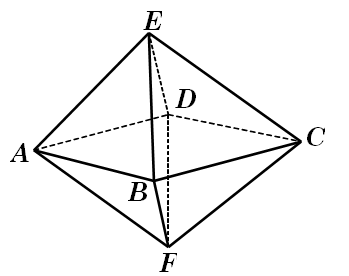
Chọn B.
Câu 22. Có tất cả bao nhiêu mặt phẳng cách đều bốn đỉnh của một tứ diện?
A. mặt phẳng. B. mặt phẳng.
C. mặt phẳng. D. Có vô số mặt phẳng.
Có loại mặt phẳng thỏa mãn đề bài là:
Loại 1: Mặt phẳng qua trung điểm của cạnh bên có chung đỉnh. Có 4 mặt phẳng thỏa mãn loại này (vì có 4 đỉnh)
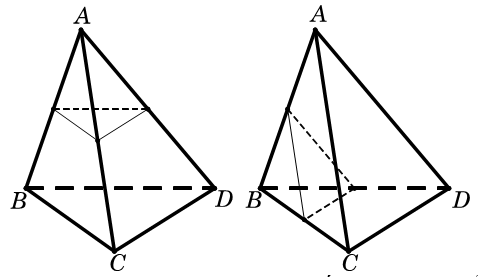
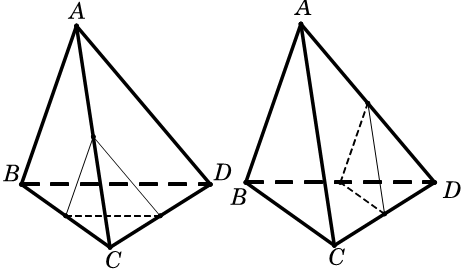
Nhận xét. Loại này ta thấy có 1 điểm nằm khác phía với 3 điểm còn lại.
Loại 2: Mặt phẳng qua trung điểm của cạnh ( cạnh này thuộc cặp cạnh, mỗi cặp cạnh là chéo nhau). Có mặt phẳng như thế.
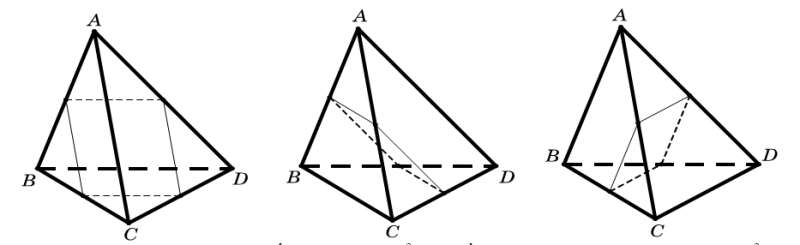
Nhận xét. Loại này ta thấy có 2 điểm nằm khác phía với 2 điểm còn lại.
Chọn C.
Câu 23.(ĐỀ CHÍNH THỨC 2016 – 2017) Mặt phẳng AB'C' chia khối lăng trụ ABC.A'B'C' thành các khối đa diện nào ?
A. Một khối chóp tam giác và một khối chóp tứ giác.
B. Hai khối chóp tam giác.
C. Một khối chóp tam giác và một khối chóp ngũ giác.
D. Hai khối chóp tứ giác.
Dựa vào hình vẽ, ta thấy mặt phẳng AB'C' chia khối lăng trụ ABC.A'B'C' thành khối chóp tam giác A.A'B'C' và khối chóp tứ giác A.BCC'B'.
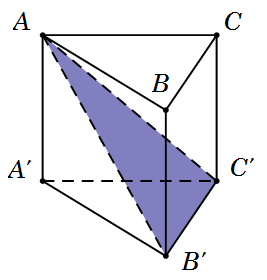
Chọn A.
Câu 24. Lắp ghép hai khối đa diện H1,H2 để tạo thành khối đa diện H, trong đó H1 là khối chóp tứ giác đều có tất cả các cạnh bằng a, H2 là khối tứ diện đều cạnh a sao cho một mặt của H1 trùng với một mặt của H2 như hình vẽ. Hỏi khối da diện H có tất cả bao nhiêu mặt?
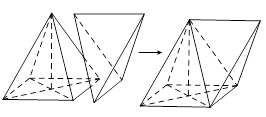
A. 5. B. 7. C. 8. D. 9.
Khối đa diện H có đúng 5 mặt. Chọn A.
Sai lầm hay gặp: Khối chóp tứ giác đều có 5 mặt. Khối tứ diện đều có 4 mặt.
Ghép hai hình lại như hình vẽ ta được khối đa diện H có 8 mặt.
Câu 25. Có thể chia một hình lập phương thành bao nhiêu khối tứ diện bằng nhau?
A. B. C. D.
Lần lượt dùng mặt phẳng BDD'B' ta chia thành hai khối lập phương thành hai khối lăng trụ ABD.A'B'D' và BCD.B'C'D'.
Với khối ABD.A'B'D' ta lần lượt dùng các mặt phẳng AB'D' và AB'D chia thành ba khối tứ diện bằng nhau.
Tương tự với khối BCD.B'C'D'.
Vậy có tất cả 6 khối tứ diện bằng nhau. Chọn C.
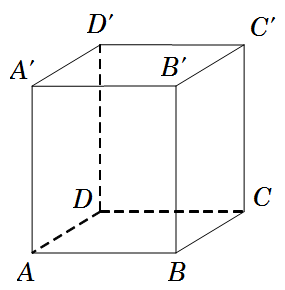
Câu 26: Trong các mệnh đề sau, mệnh đề nào đúng?
Khối đa diện có các mặt là những tam giác thì:
A. Số mặt và số đỉnh của nó bằng nhau
B. Số mặt và số cạnh của nó bằng nhau
C. Số mặt của nó là một số chẵn
D. Số mặt của nó là một số lẻ
Ta có thể dùng các phản ví dụ để loại dần các mệnh để sai. Tứ diện (có 4 đỉnh, 4 mặt và 6 cạnh) ta thấy ngay mệnh đề B và D sai.
Từ hình bát diện đều (có 6 đỉnh, 8 mặt) ta thấy mệnh đề A sai.
Vậy C là mệnh đề đúng.
Câu 27: Trong các mệnh đề sau, mệnh đề nào sai ?
A. Tồn tại một hình đa diện có số cạnh bằng 7
B. Tồn tại một hình đa diện có số cạnh nhỏ hơn 7
C. Số cạnh của một hình đa diện luôn lớn hơn hoặc bằng 6
D. Tồn tại một hình đa diện có số cạnh lớn hơn 7
Câu C luôn đúng ( theo lí thuyết).
Từ hình tứ diện suy ra câu B đúng.
Từ hình hộp suy ra câu D đúng.
Vậy câu A sai.
Câu 28: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Trong một hình đa diện tổng của số mặt và số cạnh nhỏ hơn số đỉnh.
B. Trong một hình đa diện tổng của số mặt và số đỉnh lớn hơn số cạnh
C. Trong một hình đa diện tổng số cạnh và số đỉnh nhỏ hơn số mặt
D. Tồn tại một hình đa diện có tổng của số mặt và số đỉnh nhỏ hơn số cạnhTa có thể sử dụng công thức Ơle: d + m – 2 = c suy ra B là mệnh đề đúng.
Câu 29: Trong các hình sau đây, hình nào là hình đa diện?
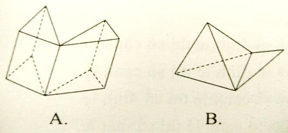
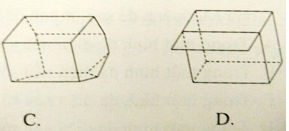
Hình A có một cạnh là cạnh chung của bốn mặt, các hình B, D có cạnh chỉ thuộc một mặt nên không phải hình đa diện.
Câu 30: Trong các hình sau đây, hình nào không phải là hình đa diện?
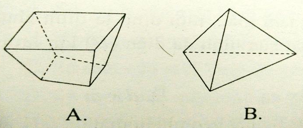
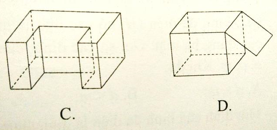
Hình D có cạnh chỉ thuộc một mặt nên không phải là hình đa diện.
Câu 31: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Mỗi hình đa diện có ít nhất 8 mặt
B. Mỗi hình đa diện có ít nhất 6 mặt
C. Mỗi hình đa diện có ít nhất 5 mặt
D. Mỗi hình đa diện có ít nhất 4 mặt
Khẳng định D đúng: mỗi hình đa diện có ít nhất 4 mặt
Câu 32: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Mỗi hình đa diện có ít nhất 8 cạnh
B. Mỗi hình đa diện có ít nhất 7 cạnh
C. Mỗi hình đa diện có ít nhất 6 cạnh
D. Mỗi hình đa diện có ít nhất 9 cạnh
Khẳng định C đúng: Mỗi hình đa diện có ít nhất 6 cạnh- đó là hình tứ diện.
Câu 33: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Mỗi hình đa diện có ít nhất 8 đỉnh
B. Mỗi hình đa diện có ít nhất 6 đỉnh
C. Mỗi hình đa diện có ít nhất 5 đỉnh
D. Mỗi hình đa diện có ít nhất 4 đỉnh
Khẳng định D đúng: Mỗi hình đa diện có ít nhất 4 đỉnh. Tứ diện có 4 đỉnh.
Câu 34: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Tồn tại một hình đa diện có số mặt lớn hơn số cạnh
B. Tồn tại một hình đa diện có số mặt lớn hơn số đỉnh
C. Trong một hình đa diện số mặt luôn lớn hơn hoặc bằng số đỉnh
D. Tồn tại một hình đa diện có số đỉnh lớn hơn số cạnh
Ta có khối bát diện đều có 8 mặt và 6 đỉnh. Do đó tồn tại khối đa diện có số mặt lớn hơn số đỉnh.
Chọn B
Câu 35 Trong các mệnh đề sau, mệnh đề nào đúng?
A. Trong một hình đa diện nếu số mặt và số đỉnh lẻ thì số cạnh chẵn
B. Trong một hình đa diện nếu số mặt và số đỉnh lẻ thì số cạnh lẻ
C. Trong một hình đa diện nếu số mặt và số cạnh lẻ thì số đỉnh lẻ
D. Trong một hình đa diện nếu số đỉnh và số cạnh lẻ thì số mặt lẻ
Ta có: Đ + M - C = 2.
Đáp án A. Nếu số M và số Đ là lẻ thì tổng số M + số Đ là chẵn. Do đó số C là chẵn. A đúng, B sai.
Đáp án C. Nếu số M và số C là lẻ thì tổng số M + số C là chẵn. Do đó số Đ là chẵn. C sai.
Đáp án D. Nếu số Đ và số C là lẻ thì tổng số Đ + số C là chẵn. Do đó số C là chẵn. D sai.
Chọn A
Câu 36: Trong các mệnh đề sau, mệnh đề nào đúng?
Cho hình đa diện (H) có các mặt là nhứng tam giác, mỗi đỉnh là đỉnh chung của đúng 3 mặt. Gọi số các đỉnh, cạnh, mặt của hình đa diện (H) lần lượt là d, c, m. Khi đó:
A. d > m B. d < m C. d = m D. d + m = c
Câu 12: Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất bao nhiêu mặt?
A. 2 mặt B. 3 mặt C. 4 mặt D. 5 mặt
Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất 3 mặt.
Câu 37: Có ít nhất bao nhiêu cạnh xuất phát từ mỗi đỉnh của một hình đa diện?
A. 5 cạnh B. 4 cạnh C. 3 cạnh D. 2 cạnh
Có ít nhất 3 cạnh xuất phát từ mỗi đỉnh của một hình đa diện.
Câu 38: Hãy chọn cụm từ (hoặc từ) cho dưới đây để sau khi điền nó vào chỗ trống mệnh đề sau trở thành mệnh đề đúng
“Số cạnh của một hình đa diện luôn….”
A. Chẵn B. Lẻ
C. Nhỏ hơn hoặc bằng số đỉnh D. Lớn hơn hoặc bằng 6
“Số cạnh của một hình đa diện luôn lớn hơn hoặc bằng 6”
Câu 39: Trong các mệnh đề sau, mệnh đề nào sai?
A. Số cạnh của một hình đa diện luôn lớn hơn hoặc bằng 6
B. Số cạnh của một hình đa diện luôn lớn hơn hoặc bằng 7
C. Số mặt của một hình đa diện luôn lớn hơn hoặc bằng 4
D. Số đỉnh của một hình đa diện luôn lớn hơn hoặc bằng 4
Mệnh đề : Số cạnh của một hình đa diện luôn lớn hơn hoặc bằng 7 là sai cần sửa thành: Số cạnh của một hình đa diện luôn lớn hơn hoặc bằng 6.
Câu 40: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Số cạnh của một hình đa diện luôn chẵn
B. Số đỉnh của một hình đa diện luôn chẵn
C. Số mặt của một hình đa diện luôn chẵn
D. Số đỉnh của một hình lăng trụ luôn chẵn
Mệnh đề: “Số đỉnh của một hình lăng trụ luôn chẵn” là đúng. Hình lăng trụ có hai đáy là hai đa giác bằng nhau. Nếu đáy là đa giác n đỉnh thì số đỉnh của hình lăng trụ là 2n.
Câu 41: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Một hình đa diện có các mặt là những tam giác thì số mặt của nó là số chẵn
B. Một hình đa diện có các mặt là những tam giác thì số mặt của nó là số lẻ
C. Tồn tại một hình đa diện có các mặt là những tam giác sao cho số mặt của nó là số lẻ
D. Tồn tại một hình đa diện có các mặt là những tam giác sao cho số mặt của nó bằng số cạnh
Nếu mỗi mặt của đa diện (H) là đa giác có đúng p cạnh thì ta có: M. p= 2C
Trong đó, M là số mặt, C là số cạnh.
Do đó, nếu một hình đa diện có các mặt là những tam giác
=> p = 3. Khi đó, 3M = 2C
Suy ra; M là số chẵn.
Câu 42: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Số cạnh của một hình lăng trụ luôn chẵn
B. Số đỉnh của một hình chop luôn chẵn
C. Số mặt của một hình lăng trụ luôn chẵn
D. Số cạnh của một hình chop luôn chẵn
Nếu hình chóp có đáy là n - đa giác thì số cạnh của hình chóp là 2n.
Do đó, số cạnh của một hình chóp luôn chẵn.
Câu 43: Hai hình đa diện bằng nhau khi và chỉ khi:
A. Có phép tịnh tiến biến hình này thành hình kia
B. Có phép dời hình biến hình này thành hình kia
C. Có các cạnh tương ứng bằng nhau
D. Có các mặt tương ứng là các đa giác bằng nhau
Hai hình đa diện bằng nhau khi và chỉ khi: Có phép dời hình biến hình này thành hình kia
Câu 44: Trong các mệnh đề sau đây mệnh đề nào đúng?
A. Tồn tại các khối đa diện đều loại (5;3)
B. Tồn tại các khối đa diện đều loại (5;4)
C. Tồn tại các khối đa diện đều loại (5;5)
D. Tồn tại các khối đa diện đều loại (4;5)
Tồn tại các khối đa diện đều loại (5;3) gọi là khối mười hai mặt đều.
Câu 45: Mỗi cạnh của một khối đa diện là cạnh chung của bao nhiêu mặt của khối đa diện:
A. Hai mặt
B. Ba mặt
C. Bốn mặt
D. Năm mặt
Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng 2 đa giác
Câu 46: Trong các mệnh đề sau mệnh đề nào sai:
A. Hình lăng trụ đều có cạnh bên vuông góc với đáy.
B. Hình lăng trụ đều có các mặt bên là các hình chữ nhật.
C. Hình lăng trụ đều có các cạnh bên bằng đường cao của lăng trụ.
D. Hình lăng trụ đều có tất cả các cạnh đều bằng nhau
Đáp án D
Phương án A. Đúng: Vì hình lăng trụ đều là hình lăng trụ đứng có đáy là đa giác đều nên lăng trụ đều có cạnh bên vuông góc với đáy.
Phương án B. Đúng.
Phương án C. Đúng.
Phương án D. Sai: Do lăng trụ đều có cạnh đáy và chiều cạnh bên có thể không bằng nhau.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.