Toptailieu.vn xin giới thiệu 50 bài tập trắc nghiệm Ôn tập chương I (có đáp án) chọn lọc, hay nhất giúp học sinh lớp 12 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán.
Mời các bạn đón xem:
Ôn tập chương I
Câu 1: Trong các mệnh đề sau đây, mệnh đề nào đúng?
A. Hai khối đa diện có thể tích bằng nhau thì bằng nhau
B. Hai khối chóp có hai đáy là hai tam giác đều bằng nhau thì thể tích bằng nhau
C. Hai khối lăng trụ có chiều cao bằng nhau thì thể tích bằng nhau
D. Hai khối đa diện bằng nhau có thể tích bằng nhau
Lời giải:
Phương án A. Sai: Xem lại định nghĩa
“Hai đa diện được gọi là bằng nhau nếu có 1 phép dời hình biến đa diện này thành đa diện kia”.
Phương án B. Sai vì Vchóp = 1/3 hSđáy nên hai chóp có thể tích bằng nhau thì cần thêm điều kiện đường cao bằng nhau.
Phương án C. Sai Vlăng trụ = h.Sđáy
Thiếu điều kiện hai đáy có diện tích bằng nhau.
Phương án D. Đúng. Vì hai khối đa diện bằng nhau được tạo thành từ một phép dời hình, nó bảo toàn khoảng cách giữa các điểm. Do đó thể tích của chúng bằng nhau.
Đáp án cần chọn là:D
Câu 2: Trong các mệnh đề sau đây mệnh đề nào đúng?
A. Tồn tại các khối đa diện đều loại (5;3)
B. Tồn tại các khối đa diện đều loại (5;4)
C. Tồn tại các khối đa diện đều loại (5;5)
D. Tồn tại các khối đa diện đều loại (4;5)
Lời giải:
Tồn tại các khối đa diện đều loại (5;3) gọi là khối mười hai mặt đều.
Đáp án cần chọn là:A
Câu 3: Mỗi cạnh của một khối đa diện là cạnh chung của bao nhiêu mặt của khối đa diện:
A. Hai mặt
B. Ba mặt
C. Bốn mặt
D. Năm mặt
Lời giải:
Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng 2 đa giác
Đáp án cần chọn là:A
Câu 4: Trong các mệnh đề sau mệnh đề nào sai:
A. Hình lăng trụ đều có cạnh bên vuông góc với đáy.
B. Hình lăng trụ đều có các mặt bên là các hình chữ nhật.
C. Hình lăng trụ đều có các cạnh bên bằng đường cao của lăng trụ.
D. Hình lăng trụ đều có tất cả các cạnh đều bằng nhau
Lời giải:
Phương án A. Đúng: Vì hình lăng trụ đều là hình lăng trụ đứng có đáy là đa giác đều nên lăng trụ đều có cạnh bên vuông góc với đáy.
Phương án B. Đúng.
Phương án C. Đúng.
Phương án D. Sai: Do lăng trụ đều có cạnh đáy và chiều cạnh bên có thể không bằng nhau.
Đáp án cần chọn là:D
Câu 5: Mỗi hình dưới đây gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó).
Số đa diện lồi trong các hình vẽ trên là:
A. 1
B. 2
C. 3
D. 4
Lời giải:
Hai đa diện lồi là hình 1 và 4.
Đáp án cần chọn là:B
Câu 6: Kim tự tháp Kê-ốp ở Ai Cập được xây dựng vào khoảng 2500 năm trước công nguyên. Kim tự tháp này là một hình chóp tứ giác đều có chiều cao là 147m, cạnh đáy dài 230m. Tính thể tích của nó
A. 2 592 100m3
B. 52900 m3
C. 7776300 m3
D. 1470000 m3
Lời giải:
Đáp án cần chọn là:A
Câu 7. Cho các hình sau:
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình đa diện là:
A. Hình 1.
B. Hình 2.
C. Hình 3.
D. Hình 4.
Lời giải:
Hình đa diện là hình tạo bởi một số hữu hạn các đa giác thỏa mãn hai tính chất sau:
1. Hai đa giác bất kì hoặc không có điểm chung hoặc chỉ có một đỉnh chung hoặc chỉ có một cạnh chung.
2. Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác.
Các hình 2, 3, 4 đều không thỏa mãn tính chất số 2.
Đáp án cần chọn là:A
Câu 8. Cho các hình sau:
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình đa diện là: Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình không phải đa diện là:
A. Hình 1.
B. Hình 2.
C. Hình 3.
D. Hình 4.
Lời giải:
Áp dụng các tính chất của hình đa diện:
+ Mỗi cạnh là cạnh chung bất kì của đúng hai mặt;
+ Hai mặt bất kì hoặc có 1 đỉnh chung, hoặc 1 cạnh chung, hoặc không có điểm chung nào.
Hình 4 không có tính chất 2: hai mặt bất kì có 1 điểm chung – nhưng điểm đó không phải là đỉnh.
Đáp án cần chọn là:D
Câu 9. Cho các hình sau:
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình đa diện là:
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), số hình đa diện là:
A. 1.
B. 2.
C. 3.
D. 4.
Lời giải:
Các hình 1; hình 3; hình 4 là các hình hữu hạn đa giác phẳng thỏa mãn 2 điều kiện:
+ Hai đa giác bất kì hoặc không có điểm chung, hoặc có 1 đỉnh chung hoặc có 1 cạnh chung
+ Mỗi cạnh của 1 đa giác là cạnh chung của đúng 2 đa giác.
Do đó, các hình 1, 3 và hình 4 là các hình đa diện.
Đáp án cần chọn là:C
Câu 10: Trong các mệnh đề sau đây, mệnh đề nào đúng?
A. Hai khối đa diện có thể tích bằng nhau thì bằng nhau
B. Hai khối chóp có hai đáy là hai tam giác đều bằng nhau thì thể tích bằng nhau
C. Hai khối lăng trụ có chiều cao bằng nhau thì thể tích bằng nhau
D. Hai khối đa diện bằng nhau có thể tích bằng nhau
Lời giải:
Phương án A. Sai: Xem lại định nghĩa
“Hai đa diện được gọi là bằng nhau nếu có 1 phép dời hình biến đa diện này thành đa diện kia”.
Phương án B. Sai vì Vchóp = 1/3 hSđáy nên hai chóp có thể tích bằng nhau thì cần thêm điều kiện đường cao bằng nhau.
Phương án C. Sai Vlăng trụ = h.Sđáy
Thiếu điều kiện hai đáy có diện tích bằng nhau.
Phương án D. Đúng. Vì hai khối đa diện bằng nhau được tạo thành từ một phép dời hình, nó bảo toàn khoảng cách giữa các điểm. Do đó thể tích của chúng bằng nhau.
Đáp án cần chọn là:D
Câu 11: Trong các mệnh đề sau đây mệnh đề nào đúng?
A. Tồn tại các khối đa diện đều loại (5;3)
B. Tồn tại các khối đa diện đều loại (5;4)
C. Tồn tại các khối đa diện đều loại (5;5)
D. Tồn tại các khối đa diện đều loại (4;5)
Lời giải:
Tồn tại các khối đa diện đều loại (5;3) gọi là khối mười hai mặt đều.
Đáp án cần chọn là:A
Câu 12: Mỗi cạnh của một khối đa diện là cạnh chung của bao nhiêu mặt của khối đa diện:
A. Hai mặt
B. Ba mặt
C. Bốn mặt
D. Năm mặt
Lời giải:
Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng 2 đa giác
Đáp án cần chọn là:A
Câu 13: Trong các mệnh đề sau mệnh đề nào sai:
A. Hình lăng trụ đều có cạnh bên vuông góc với đáy.
B. Hình lăng trụ đều có các mặt bên là các hình chữ nhật.
C. Hình lăng trụ đều có các cạnh bên bằng đường cao của lăng trụ.
D. Hình lăng trụ đều có tất cả các cạnh đều bằng nhau
Lời giải:
Phương án A. Đúng: Vì hình lăng trụ đều là hình lăng trụ đứng có đáy là đa giác đều nên lăng trụ đều có cạnh bên vuông góc với đáy.
Phương án B. Đúng.
Phương án C. Đúng.
Phương án D. Sai: Do lăng trụ đều có cạnh đáy và chiều cạnh bên có thể không bằng nhau.
Đáp án cần chọn là:D
Câu 14: Cho khối chóp S.ABC có SA = 9, SB = 4, SC = 8 và đôi một vuông góc. Các điểm A', B', C' thỏa mãn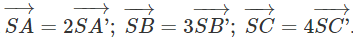 
Thể tích khối chóp S.A'B'C' là:
A. 24
B. 16
C. 2
D. 12
Lời giải:
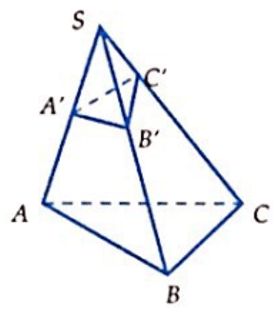
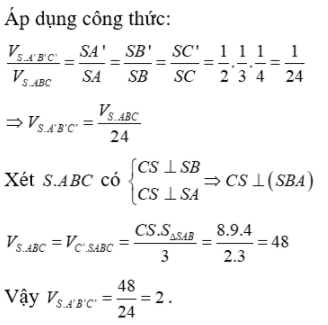
Đáp án cần chọn là:C
Câu 15: Kim tự tháp Kê-ốp ở Ai Cập được xây dựng vào khoảng 2500 năm trước công nguyên. Kim tự tháp này là một hình chóp tứ giác đều có chiều cao là 147m, cạnh đáy dài 230m. Tính thể tích của nó
A. 2 592 100m3
B. 52900 m3
C. 7776300 m3
D. 1470000 m3
Lời giải:
Đáp án cần chọn là:A
Câu 16. Số mặt phẳng đối xứng của hình tứ diện đều là:
A. 10.
B. 8.
C. 6.
D. 4.
Lời giải:
Các mặt phẳng đối xứng của hình tứ diện đều là các mặt phẳng chứa một cạnh và qua trung điểm cạnh đối diện.
Vậy hình tứ diện đều có 6 mặt phẳng đối xứng.
Đáp án cần chọn là:C
Câu 17. Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA vuông góc với (ABCD). Hình chóp này có mặt đối xứng nào?
A. Không có.
B. (SAB).
C. (SAC).
D. (SAD)
Lời giải:
Ta có:
và O là trung điểm của BD. Suy ra (SAC) là mặt phẳng trung trực của BD.
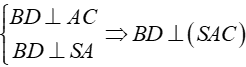
Suy ra (SAC) là mặt đối xứng của hình chóp, và đây là mặt phẳng duy nhất.
Đáp án cần chọn là:C
Câu 18. Gọi n1, n2, n3 lần lượt là số trục đối xứng của khối tứ diện đều, khối chóp tứ giác đều và khối lập phương. Mệnh đề nào sau đây là đúng?
A. n1= 0; n2 = 0; n3 = 6
B. n1 = 0; n2 = 1; n3 = 9
C. n1 = 3; n2 = 1; n3 = 9
D. n1 =0; n2= 1; n3 = 3
Lời giải:
+Khối tứ diện đều có 3 trục đối xứng (đi qua trung điểm của các cặp cạnh đối diện).
+Khối chóp tứ giác đều có 1 trục đối xứng (đi qua đỉnh và tâm của mặt tứ giác).
+Khối lập phương có 9 trục đối xứng (Loại 1: đi qua tâm của các mặt đối diện ; Loại 2: đi qua trung điểm các cặp cạnh đối diện).
Đáp án cần chọn là:C
Câu 19. Trung điểm các cạnh của một tứ diện đều là
A. Các đỉnh của một hình tứ diện đều.
B. Các đỉnh của một hình bát diện đều.
C. Các đỉnh của một hình mười hai mặt đều.
D. Các đỉnh của một hình hai mươi mặt đều.
Lời giải:
Ta chứng minh trung điểm các cạnh của một tứ diện đều là các đỉnh của một hình bát diện đều.
+ Cho tứ diện đều ABCD cạnh a.
Gọi M, N, P, I, J, K lần lượt là trung điểm của các cạnh AB, BC, CD, AC, AD, DB.
+ Ta có: IM=IN=MN=1/2a (tính chất đường trung bình của tam giác).
Suy ra tam giác IMN đều.
+ Chứng minh tương tự, ta có các tam giác IPN, IPJ, KPJ, KPN, IMJ, KMJ, KMN là các tam giác đều.
+ Tám tam giác trên tạo thành một đa diện có các đỉnh là M, N, P, I, J, K mà mỗi đỉnh là đỉnh chung của đúng tam giác đều. Do đó đa diện đó là đa diện đều loại {3; 4} tức là bát diện đều.
Đáp án cần chọn là:B
Câu 20. Chọn khẳng định đúng trong các khẳng định sau:
A. Tâm tất cả các mặt của 1 hình lập phương thì tạo thành một hình lập phương.
B. Tâm tất cả các mặt của 1 hình tứ diện đều thì tạo thành một hình tứ diện đều.
C. Tâm tất cả các mặt của 1 hình tứ diện đều thì tạo thành một hình lập phương.
D. Tâm tất cả các mặt của 1 hình lập phương thì tạo thành một hình tứ diện đều.
Lời giải:
Gọi P, I, J, K là tâm của các mặt ABD, ACD, ABC, BCD của tứ diện đều ABCD.
+ Ta có: 
+ Chứng minh tương tự ta có:
\
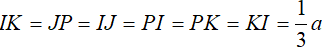
Vậy tứ diện PIJK là tứ diện đều.
Đáp án cần chọn là:B
Câu 21. Có thể chia một khối lập phương thành bao nhiêu khối tứ diện bằng nhau?
A. 2
B. 8
C. 4
D. 6
Lời giải:
Dùng mặt phẳng (BDD’B’) ta chia thành hai khối lập phương thành hai khối lăng trụ ABD.A’B’D’ và BCD.B’C’D’.
+ Với khối ABD.A’B’D’ ta lần lượt dùng các mặt phẳng ( AB’D’) và (AB’D) chia thành ba khối tứ diện bằng nhau.
+ Tương tự với khối BCD.B’C’D’, ta cũng chia được thành ba khối tứ diện đều bằng nhau.
Vậy có tất cả 6 khối tứ diện bằng nhau.
Đáp án cần chọn là:D
Câu 22. Mặt phẳng ( AB’C’) chia khối lăng trụ ABC.A’B’C’ thành các khối đa diện nào?
A. Một khối chóp tam giác và một khối chóp tứ giác.
B. Hai khối chóp tam giác.
C. Một khối chóp tam giác và một khối chóp ngũ giác.
D. Hai khối chóp tứ giác.
Lời giải:
Dựa vào hình vẽ, ta thấy mặt phẳng (AB’C’) chia khối lăng trụ ABC.A’B’C’ thành khối chóp tam giác
A.A’B’C’ và khối chóp tứ giác A.BCC’B’.
Đáp án cần chọn là:A
Câu 23. Cho khối chóp S. ABCD, hỏi hai mặt phẳng (SAC) và (SBD) chia khối chóp S. ABCD thành mấy khối chóp?
A. 4
B. 3
C. 5
D. 2
Lời giải:
Gọi O là giao điểm của AC và BD.
Mặt phẳng (SAC) và (SBD) chia khối chóp S.ABCD thành 4 khối chóp, là các khối chóp sau: S.ABO; S.ADO; S.CDO, S.BCO.
Đáp án cần chọn là:A
Câu 24. Mặt phẳng ( AB’C’) chia khối lăng trụ ABC.A’B’C’ thành các loại khối đa diện nào?
A. Hai khối chóp tam giác.
B. Một khối chóp tam giác và một khối chóp tứ giác.
C. Một khối chóp tam giác và một khối chóp ngũ giác.
D. Hai khối chóp tứ giác.
Lời giải:
Từ hình vẽ, suy ra mặt phẳng ( AB’C’) chia khối lăng trụ ABC.A’B’C’ thành một khối chóp tam giác A.A’B’C’ và một khối chóp tứ giác A.BCC’B’.
Đáp án cần chọn là:B
Câu 25. Cho tứ diện ABCD. Lấy một điểm M giữa A và B, điểm N giữa C và D. Chia tứ diện bằng 2 mặt phẳng: (MCD) và (NAB), ta chia khối đa diện đã cho thành 4 khối tứ diện:
A. AMCN;AMND; AMCD; BMCN.
B.AMCN; AMND;BMCN;BMND
C. AMCD;AMND; BMCN; BMND.
D.BMCD; BMND; AMCN;AMD.
Lời giải:
Mặt phẳng (MCD) chia chóp thành hai khối (MACD) và (MBCD)
Mặt phẳng (ABN) chia khối (MACD) thành hai khối (MANC) và (MAND).
Mặt phẳng (ABN) chia khối (MBCD) thành hai khối (MBCN) và (MBND).
Đáp án cần chọn là:B
Câu 26. Phép đối xứng qua mặt phẳng (P) biến đường thẳng d thành chính nó khi và chỉ khi
A. d song song với (P).
B. d nằm trên (P).
C. d vuông góc với (P) .
D. d nằm trên (P) hoặc d vuông góc với (P).
Lời giải:
Phép đối xứng qua mặt phẳng (P) biến đường thẳng d thành chính nó khi và chỉ khi d nằm trên (P) hoặc (d)vuông góc với (P).
Đáp án cần chọn là:D
Câu 27. Trong không gian cho hai tam giác ABC và A'B'C' bằng nhau (AB = A'B'; AC = A'C'; BC = B'C'). Chọn mệnh đề đúng trong các mệnh đề sau
A. Không thể thực hiện một phép tịnh tiến nào biến tam giác này thành tam giác kia.
B. Tồn tại duy nhất một phép tịnh tiến nào biến tam giác này thành tam giác kia.
C. Có nhiều nhất hai phép tịnh tiến nào biến tam giác này thành tam giác kia.
D. Có thể thực hiện vô số phép tịnh tiến biến tam giác này thành tam giác kia.
Lời giải:
Trước hết ta nhận thấy rằng, muốn thực hiện được một phép tịnh tiến biến ΔABC thành ΔA'B'C' thì phải có điều kiện, hai tam giác ABC và A'B'C' phải nằm trên hai mặt phẳng song song (hoặc trùng nhau) và 
Khi đó phép tịnh tiến theo vecto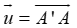 
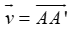
biến ΔA'B'C' thành ΔABC và phép tịnh tiến theo vecto 
biến ΔABC thành ΔA’B’C’.
Như vậy chỉ có hai phép tịnh tiến biến tam giác này thành tam giác kia.
Đáp án cần chọn là:C
Câu 28. Cho hình lập phương ABCD. A'B'C'D'. Gọi I, J lần luợt là trung điểm của các cạnh AD, BC. Phép tịnh tiến theo vecto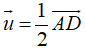 
biến tam giác A'IJ thành tam giác
A. C'CD.
B. CD'P với P là trung điểm của B'C'.
C. KDC với K là trung điểm của A’D’
D. DC'D'
Lời giải:
Gọi T là phép tịnh tiến theo vecto
Ta có
Đáp án cần chọn là:C
Câu 29. Có tất cả bao nhiêu mặt phẳng cách đều bốn đỉnh của một tứ diện?
A. 1 mặt phẳng.
B. 4 mặt phẳng.
C. 7 mặt phẳng.
D. Có vô số mặt phẳng.
Lời giải:
Có 2 loại mặt phẳng thỏa mãn đề bài là:
* Loại 1: Mặt phẳng qua trung điểm của 3 cạnh bên có chung đỉnh. Có 4 mặt phẳng thỏa mãn loại này (vì có 4 đỉnh)
Nhận xét. Loại này ta thấy có 1 điểm nằm khác phía với 3 điểm còn lại.
* Loại 2: Mặt phẳng qua trung điểm của 4 cạnh ( 4 cạnh này thuộc 2 cặp cạnh, mỗi cặp cạnh là chéo nhau). Có 3 mặt phẳng như thế.
Nhận xét. Loại này ta thấy có 2 điểm nằm khác phía với 2 điểm còn lại.
Đáp án cần chọn là:C
Câu 30. Cho phép vị tự tâm O biến điểm A thành điểm B, biết rằng OA = 2O
B. Khi đó, tỉ số vị tự là bao nhiêu?
A. 2.
B. -2.
C. 
D. 1/2
Lời giải:
Theo giả thiết OA = 2OB nên 
Vậy có hai phép vị tự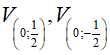 
biến điểm A thành điểm B.
Đáp án cần chọn là:C
Câu 31. Một khối đa diện lồi 11 đỉnh, 8 mặt. Vậy khối đa diện này có mấy cạnh?
A. 12.
B. 15.
C. 18.
D. 17
Lời giải:
Áp dụng định lí Ơle ta có: Đ – C+ M= 2
Thay số: 11 – C+ 8 = 2 ⇔ C= 17.
Đáp án cần chọn là:D
Câu 32. Khối 12 mặt đều {mỗi mặt là ngũ giác đều} có mấy cạnh?
A. 16.
B. 18.
C. 20.
D. 30
Lời giải:
Vì mỗi mặt là ngũ giác đều và có M mặt ( M= 12).
Áp dụng công thức: 2C= n. M trong đó n= 5 ( vì mỗi mặt là ngũ giác đều)
=> 2. C = 5. 12 ⇔ c = 5.12/2 = 30
Đáp án cần chọn là:D
Câu 33.Tổng các góc ở đỉnh của tất cả các mặt của khối đa diện đều loại {4; 3} là:
A. 4π
B. 8π
C. 12π
D. 10π
Lời giải:
Khối đa diện đều loại {4; 3} là khối lập phương, gồm 6 mặt là các hình vuông nên tổng các góc của một mặt là: 4.π/2=2π
Do đó, tổng các góc ở đỉnh của tất cả các mặt của khối đa diện là: 6.2π=12π
Đáp án cần chọn là:C
Câu 34.Cho hình bát diện đều cạnh a. Gọi S là tổng diện tích tất cả các mặt của hình bát diện đó. Mệnh đề nào dưới đây đúng?
Lời giải:
Hình bát diện đều là hình có tám mặt bằng nhau và mỗi mặt là một tam giác đều.
Gọi S0 là diện tích tam giác đều cạnh a. Diện tích tam giác đều đó là: 
Vậy diện tích S cần tính là 
Đáp án cần chọn là:C
Câu 35. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Số đỉnh và số mặt của một hình đa diện luôn bằng nhau.
B. Tồn tại hình đa diện có số đỉnh và số mặt bằng nhau.
C. Tồn tại một hình đa diện có số cạnh bằng số đỉnh.
D. Tốn tại một hình đa diện có số cạnh và mặt bằng nhau.
Lời giải:
A. Sai. Ví dụ hình lập phương có 8 đỉnh và 6 mặt.
B. Đúng. Hình tứ diện có 4 đỉnh và 4 mặt.
C. Sai. Theo công thức Ơle. Đ- C+ M= 2 => Đ+ M = 2+ C
(với Đ - là số đỉnh; C- là số cạnh; M- là số mặt).
Nếu C= Đ => M= 2 nghĩa là hình đa diện có 2 mặt, vô lý.
D. Sai. Tương tự C, nếu số C= M => Đ= 2 , vô lý.
Đáp án cần chọn là:B
Câu 36. Vật thể nào trong các vật thể sau không phải là hình đa diện?
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình đa diện là:
A. Hình A
B. Hình B
C.Hình C
D. Hình D.
Lời giải:
Hình C không thỏa mãn điều kiện: “Mỗi cạnh của một đa giác là cạnh chung của đúng hai đa giác”. Do đó, hình C không phải là hình đa diện.
Đáp án cần chọn là:C
Câu 37. Khối đa diện nào sau đây có số mặt nhỏ nhất?
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình đa diện là:
A. Khối tứ diện đều
B. Khối chóp tứ giác
C. Khối lập phương
D.Khối 12 mặt đều
Lời giải:
+ Khối tứ diện đều có bốn mặt.
+ Khối chóp tứ giác có năm mặt.
+ Khối lập phương có sáu mặt.
+ Khối 12 mặt đều có 12 mặt
Do đó, khối tứ diện đều có số mặt nhỏ nhất.
Đáp án cần chọn là:A
Câu 38: Hãy chọn cụm từ (hoặc từ) cho dưới đây để sau khi điền vào chỗ trống khẳng định sau đây trở thành khẳng định đúng:
"Số cạnh của một hình đa diện lớn luôn.......số mặt của hình đa diện ấy."
A. bằng
B. Nhỏ hơn hoặc bằng
C. nhỏ hơn
D. lớn hơn
Lời giải:
Vì trong một khối đa diện mỗi mặt có ít nhất ba cạnh và mỗi cạnh là cạnh chung của đúng hai mặt bên nên ta có 2c ≥ 3m. Suy ra c > m.
Đáp án cần chọn là:D
Câu 39: Hãy chọn cụm từ (hoặc từ) cho dưới đây để sau khi điền nó vào chỗ trống khẳng định sau trở thành khẳng định đúng:
"Số cạnh của một hình đa diện luôn..........số đỉnh của hình đa diện ấy".
A. bằng
B. lớn hơn
C. nhỏ hơn
D. nhỏ hơn hoặc bằng
Lời giải:
Vì trong một khối đa diện mỗi đỉnh có ít nhất 3 cạnh đi qua và mỗi cạnh nối hai đỉnh nên ta có 2c ≥ 3đ. Suy ra c > đ.
Đáp án cần chọn là:B
Câu 40: Khẳng định nào sau đây sai?
A. Hình lập phương là đa diện lồi.
B. Tứ diện là đa diện lồi.
C. Hình hộp là đa diện lồi.
D. Hình tạo bởi hai khối lăng trụ có chung nhau một mặt bên là một hình đa diện lồi.
Lời giải:
Hình tạo bởi hai khối lăng trụ lục giác đều bằng nhau có chung nhau một mặt bên không phải là hình đa diện lồi.
Đáp án cần chọn là:D
Câu 41: Cho một hình đa diện. Khẳng định nào sau đây là sai?
A. Mỗi đỉnh là đỉnh chung của ít nhất ba cạnh.
B. Mỗi đỉnh là đỉnh chung của ít nhất ba mặt.
C. Mỗi đỉnh là cạnh chung của ít nhất ba mặt.
D. Mỗi mặt có ít nhất ba cạnh.
Lời giải:
Dựa vào định nghĩa khối đa diện. Mỗi cạnh là cạnh chung của đúng hai mặt.
Đáp án cần chọn là:C
Câu 42: Có thể chia một hình lập phương thành bao nhiêu tứ diện bằng nhau>
A. Hai
B. Vô số
C. Bốn
D. Sáu.
Lời giải:
Mỗi hình lập phương cạnh a có thể chia thành 8 hình lập phương cạnh bằng a/2, 64 hình lập phương cạnh bằng a/4,... Do đó có thể chia một hình lập phương vô số hình lập phương bằng nhau. Mỗi hình lập phương lại có thể chia thành 6 hình tứ diện bằng nhau. Suy ra, có thể chia một hình lập phương thành vô số hình tứ diện bằng nhau.
Đáp án cần chọn là:B
Câu 43: Số cạnh của một hình bát diện đều là:
A. Tám
B. Mười
C. Mười hai
D. Mười sáu.
Lời giải:
Cách 1. Dựa vào lí thuyết: Bảng tóm tắt của năm loại khối đa diện đều.
Cách 2. Hình bát diện đều thuộc loại (3;4), nên 2c = 3 x 8, suy ra c = 12.
Đáp án cần chọn là:C
Câu 44: Số đỉnh của một hình bát diện đều là:
A. Sáu
B. Tám
C. Mười
D. Mười hai.
Lời giải:
Làm tương tự bài 1.40: 2c = 3 x 8 = 4đ, suy ra đ = 6.
Đáp án cần chọn là:A
Câu 45: Số đỉnh của hình mười hai mặt đều là:
A. Mười hai
B. Mười sáu
C. Hai mươi
D. Ba mươi.
Lời giải:
Làm tương tự bài 1.40: 2c = 5 x 12 = 3đ, suy ra đ = 20.
Đáp án cần chọn là:B
Câu 46: Số cạnh của hình mười hai mặt đều là:
A. Mười hai
B. Mười sáu
C. Hai mươi
D. Ba mươi.
Lời giải:
Làm tương tự bài 1.40: 2c = 5 x 12, suy ra c = 30.
Đáp án cần chọn là:D
Câu 47: Số đỉnh của hình hai mươi mặt đều là:
A. Mười hai
B. Mười sáu
C. Hai mươi
D. Ba mươi.
Lời giải:
Làm tương tự bài 1.40: 2c = 3 x 20 = 5đ, suy ra đ = 12.
Đáp án cần chọn là:A
Câu 48: Cho tứ diện ABCD. Gọi B' và C' lần lượt là trung điểm của AB và AC. Tỉ số thể tích của khối tứ diện AB'C'D và khối tứ diện ABCD bằng:
A. 1/2
B. 1/4
C. 1/6
D. 1/8.
Lời giải:
Đáp án cần chọn là:B
Câu 49: Cho hình lăng trụ ngũ giác ABCD.A'B'C'D'. Gọi A'', B'', C'', D'', E'' lần lượt là trung điểm của các cạnh AA', BB', CC', DD', EE'. Tỉ số thể tích giữa khối lăng trụ ABCDE.A''B''C''D''E'' và khối lăng trụ ABCDE.A'B'C'D' bằng:
A. 1/2
B. 1/4
C. 1/8
D. 1/10.
Lời giải:
Để ý rằng hai khối lăng trụ đó có diện tích đáy bằng nhau, tỉ số hai đường cao tương ứng bằng 1/2.
Đáp án cần chọn là:A
Câu 50: Cho hình chóp tứ giác S.ABCD có thể tích bằng V. Lấy điểm A' trên cạnh SA sao cho SA' = SA/3. Mặt phẳng qua A' và song song với đáy của hình chóp cắt cạnh SB, SC, SD lần lượt tại B', C', D'. Thể tích hình chóp S.A'B'C'D' bằng:
A. V/3
B. V/9
C. V/27
D. V/81.
Lời giải:
Đáp án cần chọn là:C
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.
