Toptailieu.vn giới thiệu Giải bài tập Toán lớp 7 Bài 3: Phép tính lũy thừa với số mũ tự nhiên của một số hữu tỉ sách Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7 Tập 1. Mời các bạn đón xem:

Giải SGK Toán 7 Bài 3 (Cánh diều): Phép tính lũy thừa với số mũ tự nhiên của một số hữu tỉ

Khởi động trang 17 Toán lớp 7:

Khối lượng Trái Đất khoảng 5,9724 . 1024 kg.

Khối lượng Sao Hỏa khoảng 6,417 . 1023 kg.

(Nguồn: https://www.nasa.gov)

Khối lượng Sao Hỏa bằng khoảng bao nhiêu lần khối lượng Trái Đất?

Lời giải:

Khối lượng Sao Hỏa bằng số lần khối lượng Trái Đất là:

$\frac{6,417 . {10}^{23}}{5,9724 . {10}^{24}} = \frac{6,417}{5,9724 . 10} = \frac{6,417}{59,724} \approx 0,107 \left(lần\right).$ 

Vậy khối lượng Sao Hỏa bằng khoảng 0,107 lần khối lượng Trái Đất

Hoạt động 1 trang 17 Toán lớp 7: Viết các tích sau dưới dạng lũy thừa và nêu cơ số, số mũ của chúng:

a) 7 . 7 . 7 . 7. 7;

b)  

Lời giải:

a) Ta có: 7 . 7 . 7 . 7. 7 = 75.

Lũy thừa 75 có cơ số là 7 và số mũ là 5.

b) 

Lũy thừa 12n có cơ số là 12 và số mũ là n.

Luyện tập 1 trang 18 Toán lớp 7: Tính thể tích một bể nước dạng hình lập phương có độ dài cạnh là 1,8 m.

Lời giải:

Thể tích một bể nước dạng hình lập phương có độ dài cạnh là 1,8 m là:

1,8 . 1,8 . 1,8 = 1,83 = 5,832 ($m^3$)

Vậy thể tích một bể nước dạng hình lập phương có độ dài cạnh là 1,8 m là 5,832 $m^3$.

Luyện tập 2 trang 18 Toán lớp 7: Tính:

${\left(\frac{-3}{4}\right)}^3;{\left(\frac{1}{2}\right)}^5$ .

Lời giải:

Ta có:

${\left(\frac{-3}{4}\right)}^3=\frac{-3}{4}.\frac{-3}{4}.\frac{-3}{4}=\frac{(-3).(-3).(-3)}{4.4.4}=\frac{-27}{64};$

${\left(\frac{1}{2}\right)}^5=\frac{1}{2}.\frac{1}{2}.\frac{1}{2}.\frac{1}{2}.\frac{1}{2}=\frac{1.1.1.1.1}{2.2.2.2.2}=\frac{1}{32}.$

Vậy ${\left(\frac{-3}{4}\right)}^3=\frac{-27}{64}; {\left(\frac{1}{2}\right)}^5=\frac{1}{32}.$

Hoạt động 2 trang 18 Toán lớp 7: Viết kết quả của mỗi phép tính sau dưới dạng một lũy thừa:

a) $2^m.2^n$;

b) $3^m:3^n$ với m ≥ n.

Lời giải:

a) Phép tính $2^m.2^n$ là phép nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ.

Do đó: $2^m.2^n$ = $2^{m+n}$

b) Phép tính $3^m:3^n$ (với m ≥ n) là phép chia hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và trừ các số mũ.

Do đó: $3^m:3^n$ = $3^{m-n}$ (với m ≥ n).

Luyện tập 3 trang 19 Toán lớp 7: Viết kết quả mỗi phép tính sau dưới dạng một lũy thừa:

a) $\frac{6}{5}.{\left(\mathrm{1,2}\right)}^8$;

b) ${\left(\frac{-4}{9}\right)}^7:\frac{16}{81}$.

Lời giải:

a) $\frac{6}{5}.{\left(\mathrm{1,2}\right)}^8=\frac{6}{5}.{\left(\frac{6}{5}\right)}^8$

$={\left(\frac{6}{5}\right)}^{1+8}={\left(\frac{6}{5}\right)}^9$;

b) ${\left(\frac{-4}{9}\right)}^7:\frac{16}{81}={\left(\frac{-4}{9}\right)}^7:{\left(\frac{-4}{9}\right)}^2$

 $={\left(\frac{-4}{9}\right)}^{7-2}={\left(\frac{-4}{9}\right)}^5$.

Hoạt động 3 trang 19 Toán lớp 7: So sánh ${\left({15}^3\right)}^2 và {15}^{3 . 2}$:

Lời giải:

Ta có: ${\left({15}^3\right)}^2 = {15}^3.{15}^3 ={15}^{3 + 3} = {15}^{3 . 2}$

Vậy ${\left({15}^3\right)}^2 = {15}^{3 . 2}$.

Luyện tập 4 trang 19 Toán lớp 7: Viết kết quả mỗi phép tính sau dưới dạng lũy thừa của a:

a) ${\left[{\left(-\frac{1}{6}\right)}^3\right]}^4$ với $a=-\frac{1}{6}$;

b) ${\left[{\left(-\mathrm{0,2}\right)}^4\right]}^5$ với a = − 0,2.

Lời giải:

a) Với $a=-\frac{1}{6}$ thì kết quả của phép tính ${\left[{\left(-\frac{1}{6}\right)}^3\right]}^4$ là:

${\left(a^3\right)}^4=a^{3.4}=a^{12}.$

b) Với a = − 0,2 thì kết quả của phép tính ${\left[{\left(-\mathrm{0,2}\right)}^4\right]}^5$ là:

${\left(a^4\right)}^5=a^{4.5}=a^{20}.$

Bài tập 1 trang 20 Toán lớp 7: Tìm số thích hợp cho dấu hỏi chấm trống trong bảng sau:

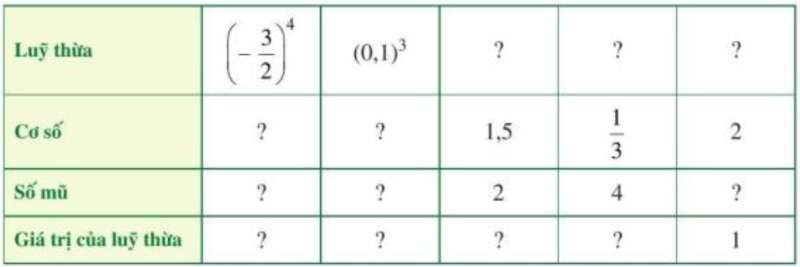
Lời giải:

+) Lũy thừa ${\left(\frac{- 3}{2}\right)}^4$

Ta có: 

$$\begin{gathered} {\left(\frac{- 3}{2}\right)}^4 = \left(\frac{- 3}{2}\right) . \left(\frac{- 3}{2}\right) . \left(\frac{- 3}{2}\right) . \left(\frac{- 3}{2}\right) \\ = \frac{( - 3 ) . ( - 3 ) . ( - 3 ) . ( - 3 )}{2.2.2.2} \\ = \frac{{( - 3 )}^4}{2^4} = \frac{81}{16} \end{gathered}$$

Do đó, lũy thừa ${\left(\frac{- 3}{2}\right)}^4$ có cơ số là $\left(\frac{- 3}{2}\right)$; số mũ là 4 và có giá trị là $\frac{81}{16}$.

+) Lũy thừa ${(0,1)}^3$.

Ta có: ${(0,1)}^3$ = 0,001.

Lũy thừa ${(0,1)}^3$ có cơ số là 0,1; số mũ là 3 và có giá trị là 0,001.

+) Lũy thừa có cơ số là 1,5 và số mũ là 2 thì có lũy thừa là $1,5^2$.

Ta có: $1,5^2$ = 2,25.

Do đó, lũy thừa có cơ số là 1,5; số mũ là 2 thì có lũy thừa là $1,5^2$ và có giá trị là 2,25.

+) Lũy thừa có cơ số là $\frac{1}{3}$và số mũ là 4 thì có lũy thừa là ${\left(\frac{1}{3}\right)}^4$.

Ta có: 

$$\begin{gathered} {\left(\frac{1}{3}\right)}^4 = \left(\frac{1}{3}\right) . \left(\frac{1}{3}\right) . \left(\frac{1}{3}\right) . \left(\frac{1}{3}\right) \\ = \frac{1 . 1 . 1 . 1}{3 . 3 . 3 . 3 } \\ = \frac{1^4}{3^4} = \frac{1}{81} \end{gathered}$$.

Do đó, lũy thừa có cơ số là $\frac{1}{3}$ và số mũ là 4 thì có lũy thừa là ${\left(\frac{1}{3}\right)}^4$ và có giá trị là $\frac{1}{81}$.

+) Lũy thừa có cơ số là 2, giá trị là 1 thì có số mũ là 0.

Khi đó, lũy thừa cần tìm là $2^0$.

Vậy ta có bảng sau:

Bài tập 2 trang 20 Toán lớp 7: So sánh:

a) (− 2)4 . (− 2)5 và (− 2)12 : (− 2)3;

b) ${\left(\frac{1}{2}\right)}^2.{\left(\frac{1}{2}\right)}^6$ và ${\left[{\left(\frac{1}{2}\right)}^4\right]}^2$;

c) (0,3)8 : (0,3)2 và ${\left[{\left(\mathrm{0,3}\right)}^2\right]}^3$;

d) ${\left(-\frac{3}{2}\right)}^5:{\left(-\frac{3}{2}\right)}^2$ và ${\left(\frac{3}{2}\right)}^3$.

Lời giải:

a) Ta có: (− 2)4 . (− 2)5 = (− 2)4 + 5 = (− 2)9;

(− 2)12 : (− 2)3 = (− 2)12 – 3 = (− 2)9.

Ta thấy: (− 2)4 . (− 2)5 = (− 2)9 = (− 2)12 : (− 2)3.

Vậy (− 2)4 . (− 2)5 = (− 2)12 : (− 2)3.

b) Ta có: ${\left(\frac{1}{2}\right)}^2.{\left(\frac{1}{2}\right)}^6={\left(\frac{1}{2}\right)}^{2+6}={\left(\frac{1}{2}\right)}^8$;

${\left[{\left(\frac{1}{2}\right)}^4\right]}^2={\left(\frac{1}{2}\right)}^{4.2}={\left(\frac{1}{2}\right)}^8$.

Ta thấy ${\left(\frac{1}{2}\right)}^2.{\left(\frac{1}{2}\right)}^6={\left(\frac{1}{2}\right)}^8={\left[{\left(\frac{1}{2}\right)}^4\right]}^2$.

Vậy ${\left(\frac{1}{2}\right)}^2.{\left(\frac{1}{2}\right)}^6={\left[{\left(\frac{1}{2}\right)}^4\right]}^2$.

c) (0,3)8 : (0,3)2 và ${\left[{\left(\mathrm{0,3}\right)}^2\right]}^3$

Ta có: (0,3)8 : (0,3)2 = (0,3)8 – 2 = (0,3)6;

${\left[{\left(\mathrm{0,3}\right)}^2\right]}^3={\left(\mathrm{0,3}\right)}^{2.3}={\left(\mathrm{0,3}\right)}^6$.

Ta thấy (0,3)8 : (0,3)2 = (0,3)6 = ${\left[{\left(\mathrm{0,3}\right)}^2\right]}^3$.

Vậy (0,3)8 : (0,3)2 = ${\left[{\left(\mathrm{0,3}\right)}^2\right]}^3$.

d) ${\left(-\frac{3}{2}\right)}^5:{\left(-\frac{3}{2}\right)}^2$ và ${\left(\frac{3}{2}\right)}^3$.

Ta có ${\left(-\frac{3}{2}\right)}^5:{\left(-\frac{3}{2}\right)}^3={\left(-\frac{3}{2}\right)}^{5-3}={\left(-\frac{3}{2}\right)}^2={\left(\frac{3}{2}\right)}^2$;

Vậy ${\left(-\frac{3}{2}\right)}^5:{\left(-\frac{3}{2}\right)}^3={\left(\frac{3}{2}\right)}^2$.

Bài tập 3 trang 20 Toán lớp 7: Tìm x, biết:

a) ${(1,2)}^3$ . x = ${(1,2)}^5$;

b) ${\left(\frac{2}{3}\right)}^7 : x = {\left(\frac{2}{3}\right)}^6$.

Lời giải:

a) ${(1,2)}^3$ . x = ${(1,2)}^5$;

x = ${(1,2)}^5$ : ${(1,2)}^3$

x = ${(1,2)}^{5-3}$

x = (${(1,2)}^2$

x = 1,44.

Vậy x = 1,44.

b)  ${\left(\frac{2}{3}\right)}^7 : x = {\left(\frac{2}{3}\right)}^6$

$$\begin{gathered} x = {\left(\frac{2}{3}\right)}^7 : {\left(\frac{2}{3}\right)}^6 \\ x = {\left(\frac{2}{3}\right)}^{7-6} \\ x =\frac{2}{3}. \end{gathered}$$

Vậy $x =\frac{2}{3}$

Bài tập 4 trang 20 Toán lớp 7: Viết kết quả mỗi phép tính sau dưới dạng lũy thừa của a:

a) ${\left(\frac{8}{9}\right)}^3.\frac{4}{3}.\frac{2}{3}$ với $a=\frac{8}{9}$;

b) ${\left(\frac{1}{4}\right)}^7.\mathrm{0,25}$ với a = 0,25;

c) ${(-\mathrm{0,125})}^6:\frac{-1}{8}$ với $a=-\frac{1}{8}$;

d) ${\left[{\left(\frac{-3}{2}\right)}^3\right]}^2$ với $a=\frac{-3}{2}$.

Lời giải:

a) Ta có ${\left(\frac{8}{9}\right)}^3.\frac{4}{3}.\frac{2}{3}={\left(\frac{8}{9}\right)}^3.\left(\frac{4}{3}.\frac{2}{3}\right)={\left(\frac{8}{9}\right)}^3.\frac{8}{9}={\left(\frac{8}{9}\right)}^{3+1}={\left(\frac{8}{9}\right)}^4$.

Với $a=\frac{8}{9}$ thì kết quả của phép tính ${\left(\frac{8}{9}\right)}^4$ là a4.

Vậy với $a=\frac{8}{9}$ thì kết quả của phép tính  ${\left(\frac{8}{9}\right)}^3.\frac{4}{3}.\frac{2}{3}$ là a4.

b) ${\left(\frac{1}{4}\right)}^7.\mathrm{0,25}$ và a = 0,25;

Ta có ${\left(\frac{1}{4}\right)}^7.\mathrm{0,25}={\left(\mathrm{0,25}\right)}^7.\mathrm{0,25}={\left(\mathrm{0,25}\right)}^{7+1}={\left(\mathrm{0,25}\right)}^8$.

Với a = 0,25 thì kết quả của phép tính (0,25)8 là a8.

Vậy với a = 0,25 thì kết quả của phép tính ${\left(\frac{1}{4}\right)}^7.\mathrm{0,25}$ là a8.

c) Ta có ${(-\mathrm{0,125})}^6:\frac{-1}{8}={\left(\frac{-1}{8}\right)}^6:\frac{-1}{8}={\left(\frac{-1}{8}\right)}^{6-1}={\left(\frac{-1}{8}\right)}^5$.

Với $a=-\frac{1}{8}$ thì kết quả của phép tính ${\left(\frac{-1}{8}\right)}^5$ là a5.

Vậy với $a=-\frac{1}{8}$ thì kết quả của phép tính ${(-\mathrm{0,125})}^6:\frac{-1}{8}$ là a5.

d) Ta có ${\left[{\left(\frac{-3}{2}\right)}^3\right]}^2={\left(\frac{-3}{2}\right)}^{3.2}={\left(\frac{-3}{2}\right)}^6$.

Với $a=\frac{-3}{2}$ thì kết quả của phép tính ${\left(\frac{-3}{2}\right)}^6$ là a6.

Vậy với $a=\frac{-3}{2}$ thì kết quả của phép tính ${\left[{\left(\frac{-3}{2}\right)}^3\right]}^2$ là a6.

Bài tập 5 trang 20 Toán lớp 7: Cho x là số hữu tỉ. Viết $x^{12}$ dưới dạng:

a) Lũy thừa của $x^2$;

a) Lũy thừa của $x^3$.

Lời giải:

a) Ta có $x^{12}=x^{2.6}={\left(x^2\right)}^6$.

Vậy x12 viết dưới dạng lũy thừa của x2 là ${\left(x^2\right)}^6$.

b) Ta có $x^{12}=x^{3.4}={\left(x^3\right)}^4$.

Vậy x12 viết dưới dạng lũy thừa của x3 là ${\left(x^3\right)}^4$ .

Bài tập 6 trang 20 Toán lớp 7: Trên bản đồ có tỉ lệ 1 : 100 000, một cánh đồng lúa có dạng hình vuông với độ dài cạnh là 0,7 cm. Tính diện tích thực tế theo đơn vị mét vuông của cánh đồng lúa đó (viết kết quả dưới dạng a . 10n với 1 ≤ a < 10)

Lời giải:

Độ dài một cạnh của cánh đồng hình vuông trên thực tế là:

0,7 . 100 000 = 70 000 (cm) = 700 (m).

Diện tích của cánh đồng hình vuông trên thực tế là:

${700}^2$ = 490 000 ($m^2$) = 4,9 . 105 ($m^2$).

Vậy diện tích thực tế của cánh đồng lúa đó là 4,9 . 105 $m^2$.

Bài tập 7 trang 20 Toán lớp 7: Biết vận tốc ánh sáng xấp xỉ bằng 299 792 458 m/s và ánh sáng Mặt Trời cần khoảng 8 phút 19 giây mới đến được Trái Đất. (Nguồn: https://vi.wikipedia.org).

Khoảng cách giữa Mặt Trời và Trái Đất xấp xỉ bằng bao nhiêu ki-lô-mét?

Lời giải:

Đổi 8 phút 19 giây = 499 giây.

Khoảng cách giữa Mặt Trời và Trái Đất xấp xỉ bằng:

299 792 458 . 499 ≈ 1,495 964 365 . 1011 = 149 596 436,5 . 103 (m)

≈ 149 596 437 (km).

Vậy khoảng cách giữa Mặt Trời và Trái Đất xấp xỉ bằng 149 596 437 km.

Bài tập 8 trang 21 Toán lớp 7: Hai mảnh vườn có dạng hình vuông. Mảnh vườn thứ nhất có độ dài cạnh là 19,5 m. Mảnh vườn thứ hai có độ dài cạnh là 6,5 m. Diện tích mảnh vườn thứ nhất gấp bao nhiêu lần mảnh vườn thứ hai?

Lời giải:

Diện tích mảnh vườn thứ nhất là:

19,52 = 380,25 ($m^2$)

Diện tích mảnh vườn thứ hai là:

6,52 = 42,25 ($m^2$)

Diện tích mảnh vườn thứ nhất gấp mảnh vườn thứ hai số lần là:

380,25 : 42,25 = 9 (lần).

Vậy diện tích mảnh vườn thứ nhất gấp 9 lần mảnh vườn thứ hai.

Bài tập 9 trang 21 Toán lớp 7: Chu kì bán rã của nguyên tố phóng xạ uranium 238 là 4,468 . 109 năm (nghĩa là sau 4,468 . 109 năm, khối lượng của nguyên tố đó chỉ còn lại một nửa).

(Nguồn: https://vi.wikipedia.org)

a) Ba chu kì bán rã của nguyên tố phóng xạ đó là bao nhiêu năm?

b) Sau ba chu kì bán rã, khối lượng của nguyên tố phóng xạ còn lại bằng bao nhiêu phần khối lượng ban đầu?

Lời giải:

a) Thời gian ba chu kì bán rã của nguyên tố phóng xạ là:

3 . 4,468 . 109 = 13,404 . 109 (năm)

Vậy ba chu kì bán rã của nguyên tố phóng xạ là 13,404 . 109 năm.

b) Gọi m0 là khối lượng ban đầu của nguyên tố phóng xạ uranium 238.

m1, m2, m3 lần lượt là khối lượng nguyên tố phóng xạ uranium 238 còn lại sau một, hai, ba chu kì.

Sau một chu kì bán rã, khối lượng nguyên tố phóng xạ uranium 238 còn lại là: 

$m_1=\frac{1}{2}{m}_0$.

Sau hai chu kì bán rã, khối lượng nguyên tố phóng xạ uranium 238 còn lại là: 

$m_2=\frac{1}{2}{m}_1=\frac{1}{2}.\frac{1}{2}{m}_0=\frac{1}{4}{m}_0$.

Sau ba chu kì bán rã, khối lượng nguyên tố phóng xạ uranium 238 còn lại là: 

$m_3=\frac{1}{2}{m}_2=\frac{1}{2}.\frac{1}{4}{m}_0=\frac{1}{8}{m}_0$.

Vậy sau ba chu kì bán rã, khối lượng của nguyên tố phóng xạ còn lại bằng $\frac{1}{8}$ khối lượng ban đầu.

Bài tập 10 trang 21 Toán lớp 7: Người ta thường dùng các lũy thừa của 10 với số mũ nguyên dương để biểu thị những số rất lớn. Ta gọi một số hữu tỉ dương được viết theo kí hiệu khoa học (hay theo dạng chuẩn) nếu nó có dạng a . 10n với 1 ≤ a < 10 và n là một số nguyên dương. Ví dụ, khối lượng của Trái Đất viết theo kí hiệu khoa học là 5,9724 . 1024 kg.

Viết các số sau theo kí hiệu khoa học (với đơn vị đã cho):

a) Khoảng cách giữa Mặt Trăng và Trái Đất khoảng 384 400 km;

b) Khối lượng của Mặt Trời khoảng 1 989 . 1027 kg;

c) Khối lượng của Sao Mộc khoảng 1 898 . 1024 kg.

(Nguồn: https://www.nasa.gov)

Lời giải:

a) Khoảng cách giữa Mặt Trăng và Trái Đất viết theo kí hiệu khoa học là:

384 400 km = 3,844 . 105 km.

Vậy khoảng cách giữa Mặt Trăng và Trái Đất khoảng 3,844 . 105 km.

b) Khối lượng của Mặt Trời viết theo kí hiệu khoa học là:

1 989 . 1027 kg = 1,989 . 1030 kg.

Vậy khối lượng của Mặt Trời khoảng 1,989 . 1030 kg.

c) Khối lượng của Sao Mộc viết theo kí hiệu khoa học là:

1 898 . 1024 kg = 1,898 . 1027 kg.

Vậy khối lượng của Sao Mộc khoảng 1,898 . 1027 kg.

Bài tập 11 trang 21 Toán lớp 7: Sử dụng máy tính cầm tay:

Nút lũy thừa  (ở một số máy tính nút lũy thừa còn có dạng  ).

Nút phân số 

Nút dấu phẩy ngăn cách phần số nguyên và phần thập phân của số thập phân: 

Nút chuyển xuống để ghi số hoặc dấu 

Nút chuyển sang phải để ghi số hoặc dấu 

Dùng máy tính cầm tay để tính:

a) ${(3,147)}^3$;

b) ${(- 23,457)}^5$;

c) ${\left(\frac{4}{-5}\right)}^4$;

d) ${(0,12)}^2 . {\left(\frac{-13}{28}\right)}^5$.

Lời giải:

Sử dụng máy tính cầm tay, ta tính được:

a) ${(3,147)}^3$ = 31,16665752;

b) ${(- 23,457)}^5$ = − 7101700,278;

c) ${\left(\frac{4}{-5}\right)}^4=\frac{256}{625}$;

d) ${(0,12)}^2 . {\left(\frac{-13}{28}\right)}^5=- 3,106626889 . {10}^{-4} .$