Với Giải SBT Toán 10 Tập 1 trong Bài tập cuối chương II Sách bài tập Toán lớp 10 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10.
Một xưởng sản xuất có 12 tấn nguyên liệu A và 8 tấn nguyên liệu B để sản xuất hai loại sản phẩm X, Y
Bài 9 trang 36 SBT Toán 10 Tập 1: Một xưởng sản xuất có 12 tấn nguyên liệu A và 8 tấn nguyên liệu B để sản xuất hai loại sản phẩm X, Y. Để sản xuất một tấn sản phẩm X cần dùng 6 tấn nguyên liệu A và 2 tấn nguyên liệu B, khi bán lãi được 10 triệu đồng. Để sản xuất một tấn sản phẩm Y cần dùng 2 tấn nguyên liệu A và 2 tấn nguyên liệu B, khi bán lãi được 8 triệu đồng. Hãy lập kế hoạch sản xuất cho xưởng nói trên sao cho có tổng số tiền lãi cao nhất.
Lời giải:
Gọi x và y lần lượt là số tấn sản phẩm X và Y mà xưởng cần sản xuất (x ≥ 0, y ≥ 0) (1).
Để sản xuất x tấn sản phẩm X cần 6x tấn nguyên liệu A, 2x tấn nguyên liệu B.
Để sản xuất y tấn sản phẩm Y cần 2y tấn nguyên liệu A, 2y tấn nguyên liệu B.
Do xưởng sản xuất có 12 tấn nguyên liệu A và 8 tấn nguyên liệu B nên 6x + 2y ≤ 12 và 2x + 2y ≤ 8.
Ta có 6x + 2y ≤ 12 ⇔ 3x + y ≤ 6. (2)
2x + 2y ≤ 8 ⇔ x + y ≤ 4. (3)
Từ đó ta có hệ bất phương trình sau: {3x+y≤6x+y≤4x≤0y≤0.
Biểu diễn miền nghiệm của hệ bất phương trình ta được miền tứ giác OABC có tọa độ các đỉnh là: O(0; 0), A(0; 4), B(1; 3), C(2; 0) (miền không bị gạch trong hình sau kể cả bờ).
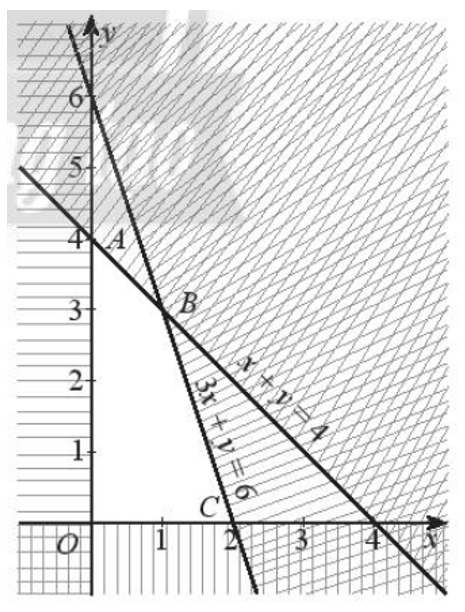
Số tiền lãi khi bán x sản phẩm X và y sản phẩm Y là F = 10x + 8y (triệu đồng).
Người ta chứng minh được rằng F đạt GTLN tại các đỉnh của tứ giác OABC.
Ta có: F(0; 0) = 10 . 0 + 8 . 0 = 0
F(0; 4) = 10 . 0 + 8 . 2 = 32
F(1; 3) = 10 . 1 + 8 . 3 = 34
F(2; 0) = 10 . 2 + 8 . 0 = 20
Do đó, F đạt GTLN là 34 triệu đồng tại đỉnh B(1; 3).
Vậy xưởng cần sản xuất 1 tấn sản phẩm X và 3 tấn sản phẩm Y thì sẽ có tổng tiền lãi cao nhất.
Xem thêm các bài giải sách bài tập Toán lớp 10 sách Chân trời sáng tạo hay, chi tiết khác:
Bài 1 trang 34 SBT Toán 10 Tập 1: Bạn Danh để dành được 900 nghìn đồng. Trong một đợt ủng hộ trẻ em mồ côi,
Bài 3 trang 34 SBT Toán 10 Tập 1: Miền không bị gạch chéo (không kể bờ d) trong Hình 1 là miền nghiệm của bất phương trình nào
Bài 4 trang 36 SBT Toán 10 Tập 1: Trên miền đa giác không gạch chéo ở Hình 6, hãy:
Bài 5 trang 36 SBT Toán 10 Tập 1: Bác Dũng dự định quy hoạch x sào đất trồng cà tím và y sào đất trồng cà chua.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.