Toán 11 Bài 1: Quy tắc đếm | Giải Toán lớp 11

Trần Thị Hường Ngày: 20-05-2022 Lớp 11

747

Toptailieu.vn giới thiệu Giải bài tập Toán 11 Bài 1: Quy tắc đếm chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập về quy tắc đếm lớp 11.

Giải bài tập Toán 11 Bài 1: Quy tắc đếm

Trả lời câu hỏi giữa bài:

Câu hỏi 1 trang 44 SGK Đại số và Giải tích 11: Trong ví dụ 1, kí hiệu A là tập hợp các quả cầu trắng, B là tập hợp các quả cầu đen. Nêu mối quan hệ giữa số cách chọn một quả cầu và số các phần tử của hai tập A, B.

Lời giải:

Trong hộp có 6 bóng trắng và 3 quả bóng đen

Tức là: |A|=6 và |B| = 3 (kí hiệu |A| là số phần tử của tập hợp A).

Chọn 1 quả cầu: Nếu chọn quả trắng thì có 6 lựa chọn, nếu chọn quả đen có 3 lựa chọn.

Vậy số cách chọn một quả cầu là: 6+3 = 9 (cách) cũng là tổng số phần tử của A và của B.

Câu hỏi 2 trang 45 SGK Đại số và Giải tích 11: Từ thành phố A đến thành phố B có ba con đường, từ B đến C có bốn con đường (h.25). Hỏi có bao nhiêu cách đi từ A đến C, qua B?

Lời giải:

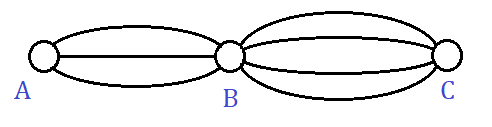
* Từ A đến B có 3 cách

Sau đó:

* Từ B đến C có 4 cách

Áp dụng quy tắc nhân ta có: 3.4 = 12 cách đi từ A đến C, qua B.

Bài tập trang 46 SGK Toán 11

Bài 1 trang 46 SGK Đại số và Giải tích 11: Từ các chữ số 1, 2, 3, 4 có thể lập được bao nhiêu số tự nhiên gồm:

a) Một chữ số ?

b) Hai chữ số ?

c) Hai chữ số khác nhau ?

Phương pháp giải:

a) Liệt kê và đếm.

b) Số tự nhiên cần lập có dạng $\bar{a b}$ , với $a, b \in {1, 2, 3, 4}$ .

+) Tìm số cách chọn cho chữ số a.

+) Tìm số cách chọn cho chữ số b.

+) Sử dụng quy tắc nhân.

c) Số tự nhiên cần lập có dạng $\bar{a b}$ , với $a, b \in {1, 2, 3, 4} (a \neq b)$ .

+) Tìm số cách chọn cho chữ số a.

+) Tìm số cách chọn cho chữ số b.

+) Sử dụng quy tắc nhân.

Lời giải:

a) Một chữ số ?

Có $4$ số là 1, 2, 3, 4.

Cách khác:

Gọi số có 4 chữ số là a.

Có 4 cách chọn a nên có tất cả 4 số cần tìm.

b) Hai chữ số ?

Số tự nhiên cần lập có dạng , với $a, b \in {1, 2, 3, 4}$ có kể đến thứ tự.

+) a có $4$ cách chọn.

+) b có $4$ cách chọn.

Vậy theo quy tắc nhân có $4.4 = 16$ (số).

c) Hai chữ số khác nhau ?

Số tự nhiên cần lập có dạng $\bar{a b}$ , với $a, b \in {1, 2, 3, 4}$ và $a, b$ phải khác nhau, có kể đến thứ tự.

+) a có $4$ cách chọn.

+) b $\neq$ a nên có $3$ cách chọn.

Vậy theo quy tắc nhân có $4.3 = 12$ (số).

Bài 2 trang 46 SGK Đại số và Giải tích 11: Từ các chữ số

1, 2, 3, 4, 5, 6

có thể lập được bao nhiêu số tự nhiên bé hơn

100

Phương pháp giải:

Số tự nhiên nhỏ hơn 100 là số tự nhiên có 1 hoặc 2 chữ số.

+) Tìm số các số tự nhiên có 1 chữ số lập được từ các số 1; 2; 3; 4; 5; 6.

+) Tìm số các số tự nhiên có 2 chữ số lập được từ các số 1; 2; 3; 4; 5; 6.

+) Sử dụng quy tắc cộng.

Lời giải:

TH1: Có $6$ số tự nhiên có 1 chữ số lập từ 1, 2, 3, 4, 5, 6.

TH2: Từ các chữ số $1, 2, 3, 4, 5, 6$ lập số tự nhiên có hai chữ số.

Gọi số tự nhiên có hai chữ số là $\bar{a b} (a \neq 0)$ .

Có 6 cách chọn chữ số a.

Có 6 cách chọn chữ số b.

Áp dụng quy tắc nhân có $6^{2} = 36$ số tự nhiên có hai chữ số lập được từ các chữ số 1, 2, 3, 4, 5, 6.

Theo quy tắc cộng có $6 + 36 = 42$ (số).

Lưu ý:

+) Các chữ số ở các hàng có thể giống nhau

+) số tự nhiên nhỏ 100 tức là các số có 1 chữ số hoặc 2 chữ số (lập từ các chữ số cho trước)

Bài 3 trang 46 SGK Đại số và Giải tích 11: Các thành phố

A, B, C, D

được nối với nhau bởi các con đường như hình 26. Hỏi:

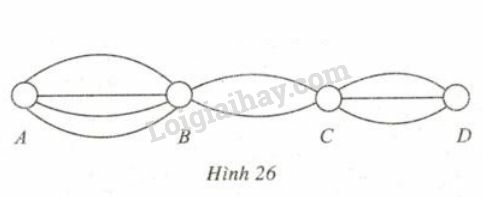
a) Có bao nhiêu cách đi từ $A$ đến $D$ mà qua $B$ và $C$ chỉ một lần ?

b) Có bao nhiêu cách đi từ đến rồi quay lại ?

Phương pháp giải:

Sử dụng quy tắc cộng và quy tắc nhân phù hợp.

Lời giải:

a) Để đi từ $A$ đến $D$ mà qua $B$ và $C$ chỉ một lần, phải thực hiện liên tiếp ba hành động sau đây:

Hành động 1: Đi từ $A$ đến $B$ . Có $4$ cách để thực hiện hành động này.

Hành động 2: Đi từ $B$ đến $C$ . Có $2$ cách để thực hiện hành động này.

Hành động 3: Đi từ $C$ đến $D$ . Có $3$ cách để thực hiện hành động này.

Theo quy tắc nhân suy ra số các cách để đi từ $A$ đến $D$ mà qua $B$ và $C$ chỉ một lần là $4.2.3 = 24$ (cách).

b) Khi đi từ $A$ đến $D$ rồi quay về $A$ nghĩa là công việc được thực hiện qua 2 hành động:

+) Từ $A$ đến $D$ qua $B$ , $C$ chỉ 1 lần có 24 cách.

+) Từ $D$ về $A$ qua $C$ , $B$ chỉ 1 lần có 24 cách.

Áp dụng quy tắc nhân, số các cách để đi từ $A$ đến $D$ (mà qua $B$ và $C$ chỉ một lần), rồi quay lại $A$ (mà qua $C$ và $B$ chỉ một lần) là:

$24.24 = 576$ (cách).

Bài 4 trang 46 SGK Đại số và Giải tích 11: Có ba kiểu mặt đồng hồ đeo tay (vuông, tròn, elip) và bốn kiểu dây (kim loại, da, vải và nhựa). Hỏi có bao nhiêu cách chọn một chiếc đồng hồ gồm một mặt và một dây ?

Phương pháp giải:

+) Tìm số cách chọn mặt đồng hồ.

+) Tìm số cách chọn dây.

+) Sử dụng quy tắc nhân.

Lời giải:

Có 3 cách chọn mặt đồng hồ.

Có 4 bốn cách chọn dây.

Vậy theo quy tắc nhân có $3.4 = 12$ cách để chọn một chiếc đồng hồ gồm một mặt và một dây.

Lý thuyết quy tắc đếm

Đóng vai trò quan trọng trong Đại số tổ hợp và trong nhiều ứng dụng

1. Quy tắc cộng

Quy tắc:

Có $k$ phương án $A_{1}, A_{2}, A_{3}, . . ., A_{k}$ để thực hiện công việc. Trong đó:

- Có $n_{1}$ cách thực hiện phương án $A_{1}$ ,

- Có $n_{2}$ cách thực hiện phương án $A_{2}$

…

- Có $n_{k}$ cách thực hiện phương án $A_{k}$ .

Khi đó, số cách để thực hiện công việc là: $n_{1} + n_{2} + . . . + n_{k}$ cách.

Nếu A và B là hai tập hợp hữu hạn không giao nhau thì số phần tử của $A \cup B$ bằng tổng số phần tử của $A$ và của $B$ , tức là: $|A \cup B| = |A| + |B|$ .

Ví dụ: Đi từ Hà Nội vào TP. Hồ Chí Minh có thể đi bằng ô tô, tàu hỏa, máy bay. Biết có $10$ chuyến ô tô, $2$ chuyến tàu hỏa và $1$ chuyến máy bay có thể vào được TP. Hồ Chí Minh. Số cách có thể đi để vào TP. Hồ Chí Minh từ Hà Nội là:

Hướng dẫn:

Có $3$ phương án đi từ Hà Nội vào TP. Hồ Chí Minh là: ô tô, tàu hỏa, máy bay.

- Có $10$ cách đi bằng ô tô (vì có $10$ chuyến).

- Có $2$ cách đi bằng tàu hỏa (vì có $2$ chuyến).

- Có $1$ cách đi bằng máy bay (vì có $1$ chuyến).

Vậy có tất cả $10 + 2 + 1 = 13$ cách đi từ HN và TP.HCM.

2. Quy tắc nhân

Có $k$ công đoạn $A_{1}, A_{2}, . . ., A_{k}$ để thực hiện công việc.

- Có $n_{1}$ cách thực hiện công đoạn $A_{1}$ .

- Có $n_{2}$ cách thực hiện công đoạn $A_{2}$ .

…

- Có $n_{k}$ cách thực hiện công đoạn $A_{k}$ .

Khi đó, số cách để thực hiện công việc là: $n_{1} . n_{2} . . . . . n_{k}$ cách.

Ví dụ: Mai muốn đặt mật khẩu nhà có $4$ chữ số. Chữ số đầu tiên là một trong $3$ chữ số $1; 2; 0$ , chữ số thứ hai là một trong $3$ chữ số $6; 4; 3$ , chữ số thứ ba là một trong $4$ chữ số $9; 1; 4; 6$ và chữ số thứ tư là một trong $4$ chữ số $8; 6; 5; 4$ . Có bao nhiêu cách để Mai đặt mật khẩu nhà?