Lời giải:

Các kết quả có thể xảy ra của phép thử gieo một con súc sắc là: xuất hiện mặt 1 chấm, 2 chấm, 3 chấm, 4 chấm, 5 chấm, 6 chấm.

Bài tập trang 63, 64 SGK Toán 11

a) Mô tả không gian mẫu

b) Xác định các biến cố:

A: "Lần đầu xuất hiện mặt sấp";

B: "Mặt sấp xảy ra đúng một lần";

C: "Mặt ngửa xảy ra ít nhất một lần".

Phương pháp giải:

Mô tả không gian mẫu bằng cách liệt kê các phần tử của không gian mẫu.

Lời giải:

a) Kí hiệu: $S$: xuất hiện mặt sấp - $M$: xuất hiện mặt ngửa

Không gian mẫu: gồm $8$ phần tử. 

$\mathrm{\Omega }=\left\{SSS;SSN;SNS;SNN;NSS;NSN;NNS;NNN\right\}$.

b)

$\begin{array}{l}A=\left\{SSS;SSN;SNS;SNN\right\}\\ B=\left\{SNN;NSN;NNS\right\}\\ C=\left\{SSN;SNS;SNN;NSS;NSN;NNS;NNN\right\}\end{array}$

a) Mô tả không gian mẫu

b) Phát biểu các biến cố sau dưới dạng mệnh đề:

$A=(6,1),(6,2),(6,3),(6,4),(6,5),(6,6);$

$B=(2,6),(6,2),(3,5),(5,3),(4,4);$

$C=(1,1),(2,2),(3,3),(4,4),(5,5),(6,6).$

Lời giải:

Phép thử $T$ được xét là: "Gieo một con súc sắc hai lần".

Không gian mẫu: $\Omega =(1;1),(1;2),(1;3),(1;4),(1;5),(1;6),(2;1),(2;2),(2;3),(2;4),(2;5),(2;6),(3;1),(3;2),(3;3),(3;4),(3;5),(3;6),(4;1),(4;2),(4;3),(4;4),(4;5),(4;6),(5;1),(5;2),(5;3),(5;4),(5;5),(5;6),(6;1),(6;2),(6;3),(6;4),(6;5),(6;6)$

Không gian mẫu có $36$ phần tử.

Cách viết khác:

$\Omega =(i,j)|i,j=1,2,3,4,5,6$

Trong đó $(i,j)$ là kết quả "lần đầu xuất hiện mặt $i$ chấm, lần sau xuất hiện mặt $j$ chấm".

b)

$A$ = "Lần gieo đầu được mặt $6$ chấm";

$B$ = "Tổng số chấm trong hai lần gieo là $8$";

$C$ = "Kết quả ở hai lần gieo là như nhau".

a) Mô tả không gian mẫu.

b) Xác định các biến cố sau:

$A$: "Tổng các số trên hai thẻ là số chẵn";

$B$: "Tích các số trên hai thẻ là số chẵn".

Phương pháp giải:

a) Mô tả không gian mẫu bằng cách liệt kê các phần tử của không gian mẫu.

b)

A là tập con của không gian mẫu sao cho tổng các số trên hai thẻ là số chẵn.

B là tập con của không gian mẫu sao cho tích các số trên hai thẻ là số chẵn.

Lời giải:

a) Phép thử $T$ được xét là: "Từ hộp đã cho, lấy ngẫu nhiên hai thẻ".

Đồng nhất mỗi thẻ với chữ số ghi trên thẻ đó, ta có: Mỗi một kết quả có thể có các phép thử  là một tổ hợp chập $2$của $4$ chữ số $1,2,3,4$.

Do đó, số phần tử của không gian mẫu là  $C_4^2=6$, và không gian mẫu gồm các phần tử sau:

$\Omega$ = $\left\{(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)\right\}$.

Chú ý:

Do hai thẻ cần chọn không phân biệt thứ tự nên cặp $(i;j)$ với $(j;i)$ là như nhau, chỉ tỉnh là 1 phần tử. Do đó không gian mẫu là $\Omega$ = $\left\{(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)\right\}$

b)

$A$ = $\left\{(1,3),(2,4)\right\}$.

$B$=$\left\{(1,2),(1,4),(2,3),(2,4),(3,4)\right\}$

$=\Omega \setminus \left\{(1,3)\right\}$.

a) Hãy biểu diễn các biến cố sau qua các biến cố $A_1,A_2$ :

$A$: "Không ai bắn trúng";

$B$: "Cả hai đều bắn trúng";

$C$: "Có đúng một người bắn trúng";

$D$: "Có ít nhất một người bắn trúng".

b)Chứng tỏ rằng $A$ = $\overline{D}$; $B$ và $C$ xung khắc.

Phương pháp giải:

a) Sử dụng các khái niệm biến cố đối, biến cố xung khắc, các phép toán trên các biến cố.

b) Sử dụng các khái niệm biến cố đối, biến cố xung khắc, các phép toán trên các biến cố.

Lời giải:

a)

Phép thử $T$ được xét là: "Hai xạ thủ cùng bắn vào bia".

Theo đề ra ta có $\overline{A_k}$ = "Người thứ $k$ không bắn trúng", $k=1,2$. Từ đó ta có:

$A$ = "Không ai bắn trúng" = "Người thứ nhất không bắn trúng và người thứ hai cũng không bắn trúng". Suy ra

$A=\overline{A_1}\cap \overline{A_2}.$

Tương tự, ta có $B$ = "Cả hai đều bắn trúng" = $A_1\cap A_2.$

Xét $C$ = "Có đúng một người bắn trúng", ta có $C$ là hợp của hai biến cố sau:

"Người thứ nhất bắn trúng và người thứ hai bắn trượt" =$A_1\cap \overline{A_2}$

"Người thứ nhất bắn trượt và người thứ hai bắn trúng" = $\overline{A_1}\cap A_2$

Suy ra $C=\left(A_1\cap \overline{A_2}\right)\cup \left(\overline{A_1}\cap A_2\right)$

Tương tự, ta có $D=A_1\cup A_2$.

b)

Ta có: biến cố $D$ là "Có ít nhất 1 người bắn trúng" tức là một trong 3 trường hợp:

+ 1 người bắn trúng và 1 người bắn không trúng

+ cả 2 người đều bắn trúng

Như vậy biến cố $\overline{D}$ là (trường hợp còn lại) "Không có ai bắn trúng" chính là biến cố $A$.

Vậy $\overline{D}=A$

Ta có: $C$ là biến cố "Có đúng 1 người bắn trúng" nghĩa là 1 người bắn trúng và 1 người không bắn trúng, khác hẳn với biến cố $B$ là "cả hai đều phải bắn trúng".

Hiển nhiên $B\cap C=\varphi$ 

Vậy theo định nghĩa thì $B$ và $C$ xung khắc với nhau.

a) Mô tả không gian mẫu.

b) Xác định các biến cố:

$A$ = "Số lần gieo không vượt quá ba";

$B$ = "Số lần gieo là bốn".

Phương pháp giải:

a) Liệt kê các phần tử.

b) Liệt kê các phần tử.

Lời giải:

a)

Không gian mẫu của phép thử đã cho là:

$\Omega =\left\{S,NS,NNS,NNNS,NNNN\right\}$

b)

$A=\left\{S,NS,NNS\right\}$;

$B=\left\{NNNS,NNNN\right\}$.

b) Xác định các biến  cố sau:

$A$: "Chữ số sau lớn hơn chữ số trước";

$B$: "Chữ số trước gấp đôi chữ số sau";

$C$: "Hai chữ số bằng nhau".

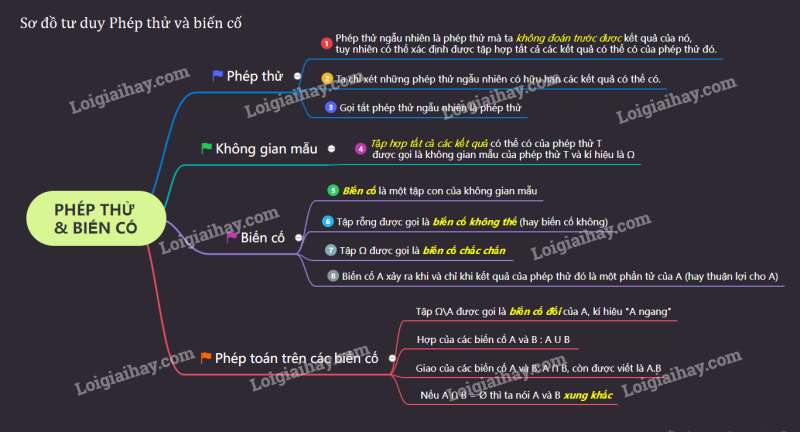
I. Phép thử ngẫu nhiên và không gian mẫu

1. Phép thử ngẫu nhiên

Phép thử ngẫu nhiên là phép thử mà ta không đoán trước được kết quả của nó, tuy nhiên có thể xác định được tập hợp tất cả các kết quả có thể có của phép thử đó.

Trong "Xác suất" ở trường phổ thông, ta chỉ xét những phép thử ngẫu nhiên có hữu hạn các kết quả có thể có.

Sau đây, ta sẽ gọi tắt phép thử ngẫu nhiên là phép thử.

2. Không gian mẫu

Tập hợp tất cả các kết quả có thể có của phép thử $T$ được gọi là không gian mẫu của phép thử $T$ và kí hiệu là $\Omega$.

Ví dụ:

Gieo một con súc sắc thì đây là môt phép thử.

Không gian mẫu $\mathrm{\Omega }=\left\{1;2;3;4;5;6\right\}$.

II. Biến cố

1. Định nghĩa

Giả sử $\Omega$ là không gian mẫu của phép thử $T$.

a) Nếu $A$ là tập con của $\Omega$ thì ta nói $A$ là biến cố (liên quan đến phép thử $T$).

b) Trong kết quả của việc thực hiện phép thử $T$, nếu có một phần tử của biến cố xảy ra thì ta nói "biến cố $A$ xảy ra".

Ví dụ:

Gieo một con súc sắc thì đây là môt phép thử.

Không gian mẫu $\mathrm{\Omega }=\left\{1;2;3;4;5;6\right\}$.

Gọi $A$ là biến cố: “Các mặt xuất hiện chẵn chấm”.

Khi đó $A=\left\{2;4;6\right\}$.

2. Biến cố không thể và biến cố chắc chắn

Giả sử $\Omega$ là không gian mẫu của phép thử $T$, ta có các định nghĩa sau:

a) Biến cố $A$ được gọi là biến cố ngẫu nhiên (liên quan đến phép thử $T$), nếu như $A$ khác rỗng và $A$ là tập con thực sự của $\Omega$.

b) Tập rỗng được gọi là biến cố không thể (liên quan đến phép thử $T$) (gọi tắt là biến cố không).

c) Tập $\Omega$ được gọi là biến cố chắc chắn (liên quan đến phép thử $T$).

3. Các quan hệ và các phép toán trên các biến cố (liên quan đến cùng một phép thử)

Giả sử $\Omega$ là không gian mẫu của phép thử $T$; $A,B,C$ là các biến cố cùng liên quan đến phép thử $T$, ta có các định nghĩa và các kết quả sau:

3.1 Hai biến cố đồng nhất

Định nghĩa:

Hai biến cố $A$ và $B$ là đồng nhất với nhau khi và chỉ khi "Tập $A$ bằng tập $B$"

Chú ý: Từ định nghĩa trực tiếp suy ra rằng hai biến cố $A$ và $B$ đồng nhất với nhau khi và chỉ khi chúng đồng thời xảy ra hoặc đồng thời cùng không xảy ra, mỗi khi phép thử $T$ được thực hiện.

Kí hiệu: $A=B$.

3.2 Hợp và giao của các biến cố

Giả sử $A,B$ là hai biến cố có liên quan đến một phép thử. Ta có định nghĩa sau:

+) Tập $A\cup B$ được gọi là hợp của các biến cố $A$ và $B$.

$A\cup B$ xảy ra khi và chỉ khi $A$ xảy ra hoặc $B$ xảy ra.

+) Tập $A\cap B$ được gọi là giao của các biến cố $A$ và $B$.

$A\cap B$ xảy ra khi và chỉ khi $A$ và $B$ đồng thời xảy ra.

Biến cố $A\cap B$ còn được viết là $A.B$.

3.3 Hai biến cố xung khắc

Hai biến cố $A$ và $B$ là xung khắc với nhau khi và chỉ khi chúng không khi nào cùng xảy ra hay $A\cap B=\mathrm{\varnothing }$.

3.4 Biến cố đối

Định nghĩa:

Nếu $A$ là biến cố liên quan đến phép thử $T$ thì tập $\Omega$ $\setminus$ $A$ cũng là một biến cố liên quan đến phép thử $T$ và được gọi là biến cố đối của biến cố $A$, kí hiệu là $\overline{A}$ .

Chú ý:

Từ định nghĩa trực tiếp suy ra:

a) $\overline{A}$ = "Không xảy ra biến cố $A$". Từ đó ta có:

($\overline{A}$ xảy ra) ⇔ ($A$ không xảy ra).

b) $\overline{A}$ là phần bù của $A$ trong $\Omega$.

c) $B$ là biến cố đối của biến cố $A$ thì $A$ là biến cố đối của biến cố $B$ ($A$ và $B$ là hai biến cố đối nhau). Đồng thời ta có:

( $A$ và  $B$ là hai biến cố đối nhau)  ⇔ $\{\begin{array}{ccc}A\cup B=\mathrm{\Omega }& & \\ A\cap B=\varphi & & \end{array}$.

Ví dụ:

Gieo một con súc sắc thì đây là môt phép thử.

Không gian mẫu $\mathrm{\Omega }=\left\{1;2;3;4;5;6\right\}$.

Gọi $A$ là biến cố: “Các mặt xuất hiện chẵn chấm”.

Khi đó $A=\left\{2;4;6\right\}$.

Gọi $B$ là biến cố: “Các mặt xuất hiện lẻ chấm”.

Khi đó $B=\left\{1;3;5\right\}$.

Dễ thấy:

$A\cup B=\mathrm{\Omega }$ và $A\cap B=\mathrm{\varnothing }$ nên $A$ và $B$ là các biến cố đối của nhau.