Toptailieu.vn giới thiệu Giải SGK Toán 10 Bài 2 (Kết nối tri thức): Tập hợp và các phép toán trên tập hợp giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 10 Tập 1. Mời các bạn đón xem:
Toán 10 Kết nối tri thức Bài 2: Tập hợp và các phép toán trên tập hợp
Hỏi: Có bao nhiêu thành viên vắng mặt trong cả hai chuyên đề?

Phương pháp giải:
Lập bảng liệt kê các thành viên và chuyên đề. Đánh dấu x nếu thành viên đó có tham gia.
Lời giải:
Ta có bảng sau:
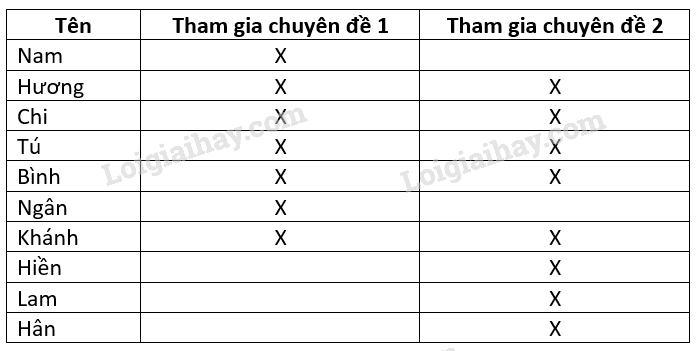
Dễ thấy: Có 10 bạn tham gia (1 chuyên đề hoặc cả hai)
Vậy có 2 thành viên vắng mặt trong cả hai chuyên đề.
1. Các khái niệm cơ bản về tập hợp
a) Nam có là một phần tử của tập hợp A không? Ngân có là một phần tử của tập hợp B không?
b) Hãy mô tả các tập hợp A và B bằng cách liệt kê các phần tử.
Phương pháp giải:
a) Nếu Nam có tên trong màn hình của chuyên đề 1 thì Nam là một phần tử của tập hợp A và ngược lại.
b) Viết tập hợp A, B bằng cách liệt kê các phần tử.
Lời giải:

a) Nam có là một phần tử của tập hợp A
Ngân không là một phần tử của tập hợp B
b) {Nam; Hương; Chi; Tú; Bình; Ngân; Khánh}
{Hương; Chi; Tú; Khánh; Bình; Hân; Hiền; Lam}
HĐ2 trang 12 SGK Toán lớp 108 Tập 1: Cho tập hợp:
C = {châu Á; châu Âu; châu Đại Dương; châu Mĩ; châu Nam Cực; châu Phi}.
a) Hãy chỉ ra tính chất đặc trưng cho các phần tử của tập hợp C.
b) Tập hợp C có bao nhiêu phần tử?
Lời giải:
a) Tính chất đặc trưng của các phần tử của tập hợp C: là các châu lục trên Trái đất.
b) Tập hợp C có 6 phần tử
Luyện tập 1 trang 13 SGK Toán lớp 10 Tập 1: Gọi X là tập nghiệm của phương trình .
Các mệnh đề sau đúng hay sai?
a)
b)
c)
Lời giải:
a) Vì nên là nghiệm của phương trình
Vậy mệnh đề “” đúng.
b) Vì nên là nghiệm của phương trình
Vậy mệnh đề “” sai.
c) Ta có:
Vậy phương trình có 2 nghiệm hay
Mệnh đề “” đúng.

Lời giải:
Ta có: {Hương; Chi; Tú; Khánh; Bình; Hân; Hiền; Lam}
và H = {Hương; Hiền; Hân}
Vậy các phần tử của H đều là phần tử của tập hợp B.
HĐ4 trang 14 SGK Toán lớp 10 Tập 1: Sơn và Thu viết tập hợp các số chính phương nhỏ hơn 100 như sau:
Sơn: {0; 1; 4; 9; 16; 25; 36; 49; 64; 81};
Thu: T = { | n là số chính phương; }.
Hỏi bạn nào viết đúng?
Phương pháp giải:
Có thể mô tả một tập hợp bằng một trong hai cách:
Cách 1: Liệt kê các phần tử của tập hợp;
Cách 2: Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp.
Lời giải:
Cả hai bạn viết đều đúng.
Sơn viết theo cách liệt kê các phần tử (số chính phương nhỏ hơn 100).
Còn Thu viết tập hợp theo cách chỉ ra tính chất đặc trưng (số chính phương và nhỏ hơn 100).
Các mệnh đề sau đúng hay sai?
a) ;
b) ;
c) .
Phương pháp giải:
Mô tả tập hợp C và tập hợp D.
So sánh các phần tử của hai tập hợp.
Lời giải:
+) Mô tả tập hợp D = {các hình vuông}
+) Mô tả tập hợp C = {các hình bình hành có hai đường chéo vuông góc} = {Các hình thoi}.
Thật vậy,
Xét tứ giác ABCD, là hình hình hành có hai đường chéo vuông góc.
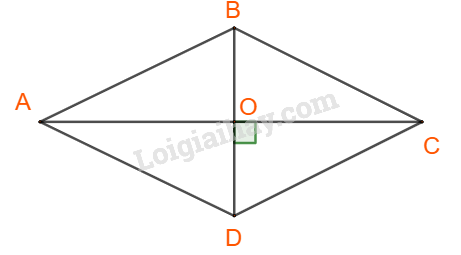
Gọi thì O là trung điểm của AC và BD.
Ta có: AO vừa là trung tuyến vừa là đường cao.
cân tại A.
.
Tương tự ta cũng có: .
Mà .
Do đó: hay tứ giác ABCD là hình thoi.
a) Vì nhiều hình thoi (các hình thoi không có góc nào vuông) thì không phải là hình vuông, nên .
Vậy mệnh đề “” sai.
b) Vì mỗi hình vuông cũng là một hình thoi (hình thoi đặc biệt: có một góc vuông), nên các phần tử của D cũng là phần tử của D. Hay
Do đó mệnh đề “” đúng.
c) Vì
Vậy mệnh đề “” sai.
2. Các tập hợp số
HĐ5 trang 15 SGK Toán lớp 10 Tập 1: Các mệnh đề sau đúng hay sai?
a) Mọi số nguyên đều viết được dưới dạng phân số
b) Tập hợp các số thực chứa tập hợp các số hữu tỉ;
c) Tồn tại một số thực không là số hữu tỉ.
Phương pháp giải:
Nhắc lại:
Lời giải:
a) Dễ thấy:
Vậy mệnh đề “Mọi số nguyên đều viết được dưới dạng phân số” đúng.
Hoặc:
Ta có; hay mỗi số nguyên cũng là một phân số.
Do đó mệnh đề “Mọi số nguyên đều viết được dưới dạng phân số” đúng.
b) Mệnh đề viết dưới dạng kí hiệu: “”, là mệnh đề đúng.
c) Mệnh đề “Tồn tại một số thực không là số hữu tỉ” đúng.
Ví dụ: ( vì ).
a) C là tập con của
b) C là tập con của
c) C là tập con của
Phương pháp giải:
C là tập con của X nếu mỗi phần tử của C đều là phần tử của X.
Lời giải:
a) Dễ thấy:
Vậy C là tập con của , mệnh đề đúng.
b) Vì nên C không là tập con của
Vậy mệnh đề sai.
c) Dễ thấy:
Vậy C là tập con của , mệnh đề đúng.
HĐ6 trang 16 SGK Toán lớp 10 Tập 1: Cho hai tập hợp C = {} và D = {}. Các mệnh đề sau đúng hay sai?
a) C, D là các tập con của ;
b) ;
c) nhưng ;
d)
Phương pháp giải:
+) nếu mọi phần tử của C đều là phần tử của .
+)
Lời giải:
a) Hiển nhiên: C, D là các tập con của .
Vậy mệnh đề này đúng.
b) Mệnh đề “” sai. Vì nhưng ;
c) Mệnh đề “ nhưng ” đúng;
d) Mệnh đề “” sai vì nhưng .
|
1) |
|
2) |
|
3) |
|
4) |
|
a) |
|
b) |
|
c) |
|
d) |
|
e) |
Lời giải:
1) . Nối với d)
2) . Nối với a)
3) . Nối với b)
4) . Nối với c)
3. Các phép toán trên tập hợp
Tập X có phải là tập con của tập A không? Tập X có phải là tập con của tập B không? (A, B là các tập hợp trong HĐ1).
Lời giải:

X = {Khánh; Bình; Hương; Chi; Tú}
A= {Nam; Hương; Chi; Tú; Bình; Ngân; Khánh}
B = {Hương; Chi; Tú; Khánh; Bình; Hân; Hiền; Lam}
Dễ thấy: Các phần tử của X đều là phần tử của tập hợp A và tập hợp B.
Do đó và .
Lời giải:
Ta có:

Giao của hai tập hợp C và D là .
Lời giải:
Kí hiệu H là tập hợp tất cả các thành viên tham gia chuyên đề 1 hoặc chuyên đề 2.
Tập hợp các bạn tham gia chuyên đề 1: A= {Nam; Hương; Chi; Tú; Bình; Ngân; Khánh}
Tập hợp các bạn tham gia chuyên đề 2: B = {Hương; Chi; Tú; Khánh; Bình; Hân; Hiền; Lam}
Vậy H = {Nam; Ngân; Hân; Hiền; Lam; Khánh; Bình; Hương; Chi; Tú }
Chú ý khi giải
Mỗi phần tử chỉ liệt kê một lần.
Lời giải:
Ta có:
A= {Nam; Hương; Chi; Tú; Bình; Ngân; Khánh}
B = {Hương; Chi; Tú; Khánh; Bình; Hân; Hiền; Lam}
Biểu đồ Ven
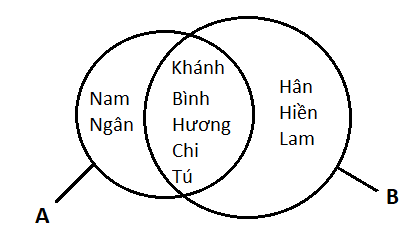
Lời giải:
A= {Nam; Hương; Chi; Tú; Bình; Ngân; Khánh}
X = {Khánh; Bình; Hương; Chi; Tú }
Có Nam và Ngân chỉ tham gia chuyên đề 1.
Tập hợp các thành viên chỉ tham gia Chuyên đề 1 mà không tham gia Chuyên đề 2 là
G = {Nam; Ngân}
Luyện tập 7 trang 18 SGK Toán lớp 10 Tập 1: Tìm phần bù của các tập hợp sau trong :
a)
b)
Phương pháp giải:
Biểu diễn các tập hợp trên trục số.
Lời giải:
Ta có:

Suy ra phần bù của tập hợp trong là:

Suy ra phần bù của tập hợp trong là:
Phương pháp giải:
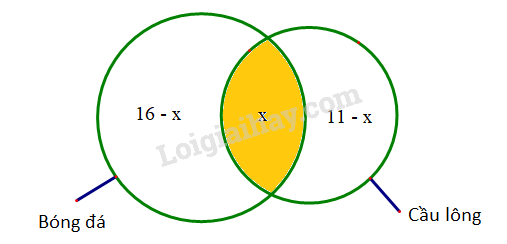
Gọi x là số bạn tham gia thi đấu cả bóng đá và cầu lông.
Sử dụng biểu đồ Ven để mô tả các tập hợp.
Lời giải:
Gọi là số bạn tham gia thi đấu cả bóng đá và cầu lông.
Ta có: 16 bạn thi đấu bóng đá và 11 bạn thi đấu cầu lông
Có bạn chỉ tham gia thi đấu bóng đá mà không thi đấu cầu lông.
Và có bạn chỉ tham gia thi đấu cầu lông mà không thi đấu bóng đá.
Ta có biểu đồ Ven như sau:
Bài tập
Phương pháp giải:
Liệt kê tên các quốc gia tiếp giáp với Việt Nam, phân cách nhau bởi dấu chấm phẩy “;”.
Biểu đồ Ven: Ghi tất cả các phần tử của tập hợp X vào tròn một đường tròn.
Lời giải:
X = {Lào; Campuchia; Trung quốc; Thái Lan}
Biểu đồ Ven:

Bài 1.9 trang 19 SGK Toán lớp 10 Tập 1: Kí hiệu E là tập hợp các quốc gia tại khu vực Đông Nam Á.
a) Nếu ít nhất hai phần tử thuộc tập hợp E.
b) Nêu ít nhất hai phần tử không thuộc tập hợp E.
c) Liệt kê các phần tử thuộc tập hợp E. Tập hợp E có bao nhiêu phần tử?
Phương pháp giải:
a) Nêu hai (hoặc nhiều hơn hai) quốc gia tại khu vực Đông Nam Á
b) Nêu hai (hoặc nhiều hơn hai) quốc gia không thuộc khu vực Đông Nam Á
c) Liệt kê tất cả các quốc gia tại khu vực Đông Nam Á
Lời giải:
a) Việt Nam ; Thái Lan ; Lào
b) Nhật Bản ; Hàn Quốc .
c) E = {Việt Nam; Lào; Campuchia; Thái Lan; Myanmar; Malaysia; Singapore; Indonesia; Brunei; Philippines; Đông Timor}
Có 11 nước thuộc khu vực Đông Nam Á. Hay tập hợp E có 11 phần tử .
Lời giải:
0; 4; 8; 12; 16 là các bội của 4 và nhỏ hơn 17.
A = { và }
Hoặc:
A = { và }
Bài 1.11 trang 19 SGK Toán lớp 10 Tập 1: Trong các tập hợp sau, tập hợp nào là tập hợp rỗng?
;
Lời giải:
Ta có:
Nhưng nên không tồn tại để
Hay .
a)
b) ;
c) ;
Lời giải:
a) Cách viết: Sai vì (là một phần tử của A) không phải là một tập hợp.
Hoặc là một phần tử của A, nên ta phải dùng kí hiệu “” thay vì “”.
Cách viết đúng:
b) Cách viết đúng, vì là một tập hợp, có duy nhất một phần tử là và
Thế nên tập hợp là một tập con của .
c) Cách viết sai vì:
là một tập hợp (tập hợp rỗng), không phải là một phần tử.
Cách viết đúng: ( Tập hợp rỗng là tập con của mọi tập hợp).
Bài 1.13 trang 19 SGK Toán lớp 10 Tập 1: Cho .Tìm để .
Phương pháp giải:
Lời giải:
Để
Tương tự, ta có:
Vậy thì .
Bài 1.14 trang 19 SGK Toán lớp 10 Tập 1: Cho và
a) Liệt kê các phần tử của hai tập hợp A và B.
b) Hãy xác định các tập hợp
Lời giải:
a)
Tập hợp B là tập các nghiệm nguyên của phương trình
Ta có:
Vậy .
b)
{ hoặc }
Bài 1.15 trang 19 SGK Toán lớp 10 Tập 1: Xác định các tập hợp sau và biểu diễn chúng trên trục số.
a)
b)
c)
d)
Phương pháp giải:
Biểu diễn các tập hợp trên trục số
Lời giải:
a) Ta có:
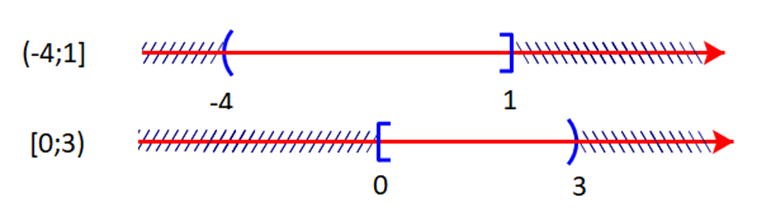
Giao của hai tập hợp là
b) Ta có:
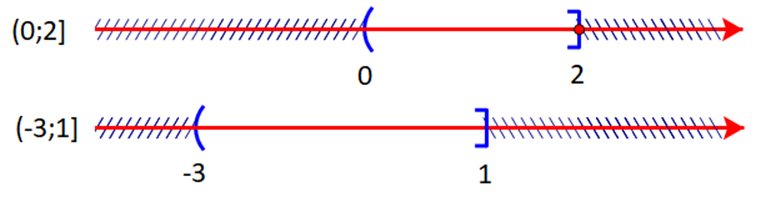
Hợp của hai tập hợp là
c) Ta có:
Giao của hai tập hợp là
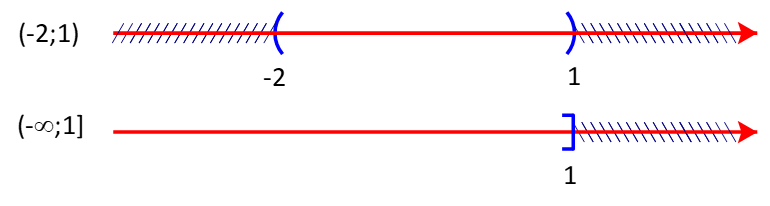
d) Ta có:

Phần bù của tập hợp trong là
a) Ban tổ chức đã huy động bao nhiêu người phiên dịch cho hội nghị đó?
b) Có bao nhiêu người chỉ phiên dịch được tiếng Anh?
c) Có bao nhiêu người chỉ phiên dịch được tiếng Pháp?
Phương pháp giải:
Sử dụng biểu đồ Ven.
Lời giải:
Gọi A là tập hợp những người phiên dịch tiếng Anh, B là tập hợp những người phiên dịch tiếng Pháp.
Ta có: , .
Biểu đồ Ven
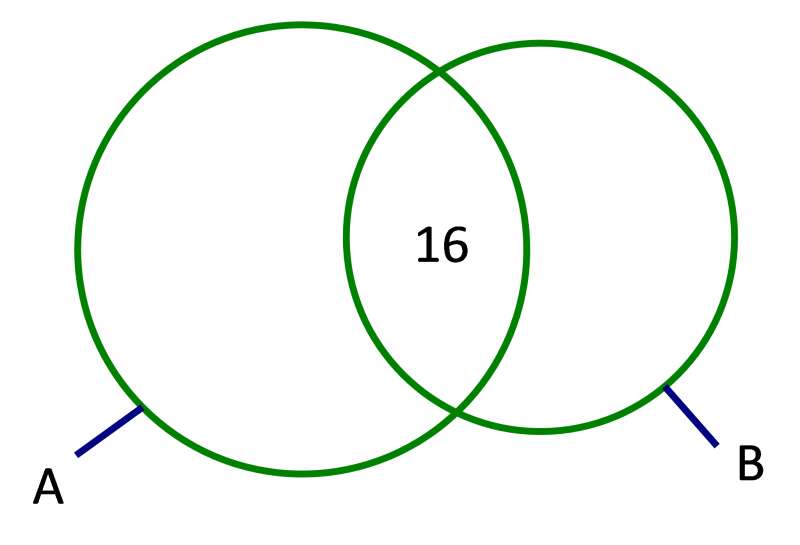
a)
Vậy ban tổ chức đã huy động 49 người phiên dịch cho hội nghị đó
b)
Vậy có 19 người chỉ phiên dịch được tiếng Anh
c)
Vậy có 14 người chỉ phiên dịch được tiếng Pháp
Lý thuyết Bài 2: Tập hợp và các phép toán trên tập hợp
1. Tập hợp
Tập hợp là một khái niệm cơ bản (không định nghĩa) của toán học.
Các tập hợp thường được kí hiệu bằng những chữ cái in hoa: . Các phần tử của tập hợp được kí hiệu bằng các chữ in thường . Kí hiệu để chỉ là một phần tử của tập hợp hay thuộc tập hợp . Ngược lại để chỉ không thuộc .
Một tập hợp có thể được cho bằng cách liệt kê các phần tử của nó hoặc được cho bằng cách nêu tính chất đặc trưng của các phần tử của nó.
Ví dụ: hay .
Một tập hợp không có phần tử nào được gọi là tập hợp rỗng, kí hiệu .
2. Biểu đồ Ven
Để minh họa một tập hợp người ta dùng một đường cong khép kín giới hạn một phần mặt phẳng. Các điểm thuộc phần mặt phẳng này chỉ các phần tử của tập hợp ấy.
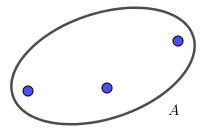
3. Tập hợp con
Ta gọi là tập hợp con của , kí hiệu
4. Hai tập hợp bằng nhau
Hai tập hợp và bằng nhau, kí hiệu , nếu tất cả các phần tử của chúng như nhau
và .
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.