Toptailieu.vn giới thiệu Giải SGK Toán 10 Bài 1 (Kết nối tri thức): Mệnh đề giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 10 Tập 1. Mời các bạn đón xem:

Toán 10 Kết nối tri thức Bài 1: Mệnh đề

1. Mệnh đề, mệnh đề chứa biến

Câu hỏi trang 6 Toán 10

HĐ1 trang 6 SGK Toán lớp 10 Tập 1:Trong các câu ở tình huống mở đầu:

a) Câu nào đúng?

b) Câu nào sai?

c) Câu nào không xác định được tính đúng sai?

Lời giải:

Các con vật xuất hiện trong hình vẽ là: Voi, ngựa, vượn, chó, mèo, chuột

a) Câu “Có 6 con vật xuất hiện trong hình vẽ” của Khoa là đúng.

b) Câu “Có 5 con vật xuất hiện trong hình vẽ” của An là sai.

c) Câu “Có bao nhiêu con vật xuất hiện trong hình vẽ?” là câu không xác định được tính đúng sai.

Luyện tập 1 trang 6 SGK Toán lớp 10 Tập 1:Thay dấu “?” bằng dấu “x” vào ô thích hợp trong bảng sau:

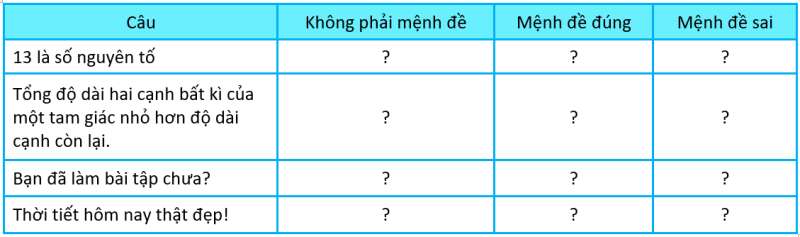
Phương pháp giải:

Bước 1: Xác định xem câu nào là mệnh đề, câu nào không là mệnh đề bằng cách:

- Mệnh đề là những câu khẳng định hoặc đúng hoặc sai

- Câu không xác định được tính đúng sai không phải là mệnh đề

Bước 2: Với những câu là mệnh đề ta đi xét tính đúng sai của mệnh đề đó.

Bước 3: Đánh dấu “x” vào ô thích hợp.

Lời giải:

“13 là số nguyên tố” là mệnh đề đúng.

“Tổng độ dài hai cạnh bất kì của một tam giác nhỏ hơn độ dài cạnh còn lại.” là mệnh đề sai.

(Giải thích: Vì theo bất đẳng thức tam giác: Trong một tam giác bất kỳ, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại.)

“Bạn đã làm bài tập chưa?”: không phải mệnh đề.

(Giải thích: Đây là câu hỏi, không xác định được tính đúng sai.)

“Thời tiết hôm nay thật đẹp!”: không phải mệnh đề.

(Giải thích: Đây là câu cảm thán, không xác định được tính đúng sai.)

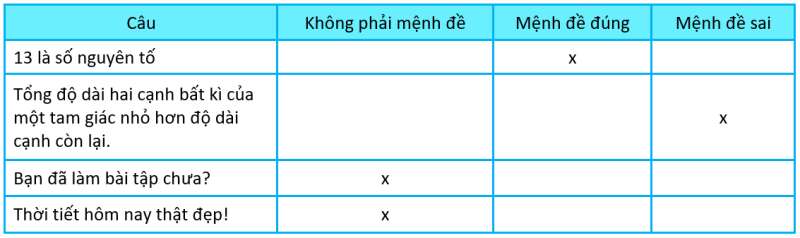
Chú ý khi giải:

+ Thông thường, các câu khẳng định có thể xác định tính đúng sai.

+ Còn các câu nghi vấn, câu cảm thán, câu cầu khiến thì không xác định được tính đúng sai nên không là mệnh đề.

Câu hỏi trang 7 Toán 10

Câu hỏi trang 7 SGK Toán lớp 10 Tập 1: Xét câu "x > 5". Hãy tìm hai giá trị thực của x để từ câu đã cho, ta nhận được một mệnh đề đúng và một mệnh đề sai.

Phương pháp giải:

Chọn hai giá trị thực của x, sao cho khi thay vào câu “x > 5” ta được một mệnh đề đúng và một mệnh đề sai.

Lời giải:

Chọn x = 6, ta được mệnh đề "6 > 5" là mệnh đề đúng.

Chọn x = 0, ta được mệnh đề “0 > 5” là mệnh đề sai

2. Mệnh đề phủ định

HĐ2 trang 7 SGK Toán lớp 10 Tập 1: Quan sát biển báo trong hình bên,

Khoa nói: “Đây là biển báo đường dành cho người đi bộ”.

An không đồng ý với ý kiến của Khoa.

Hãy phát biểu ý kiến của An dưới dạng một mệnh đề.

Phương pháp giải:

+ Mệnh đề là phát biểu có tính đúng sai.

+ Để nêu ý kiến trái ngược (dưới dạng một mệnh đề), ta có thể thêm “Không phải” vào vị trí phù hợp trong mệnh đề ban đầu.

Lời giải:

Chẳng hạn, An nói “Đây không phải là biển báo đường dành cho người đi bộ”.

Luyện tập 2 trang 7 SGK Toán lớp 10 Tập 1: Phát biểu mệnh đề phủ định của mỗi mệnh đề sau và xác định tính đúng sai của mệnh đề phủ định đó.

P: “2 022 chia hết cho 5”

Q: “Bất phương trình 2x + 1 > 0 có nghiệm”.

Phương pháp giải:

Để phủ định một mệnh đề P, ta thường thêm (hoặc bớt) từ không hoặc không phải vào trước vị ngữ của mệnh đề P. (Kí hiệu $\overline{P}$ là mệnh đề phủ định của mệnh đề P.)

Lời giải:

Mệnh đề phủ định của mệnh đề P là $\overline{P}$: “2 022 không chia hết cho 5”

Mệnh đề $\overline{P}$ đúng.

Mệnh đề phủ định của mệnh đề Q là $\overline{Q}$: “Bất phương trình $2x+1>0$ vô nghiệm”.

Mệnh đề $\overline{Q}$ sai vì bất phương trình $2x+1>0$ có nghiệm, chẳng hạn:  $x=0;x=1$.

Vận dụng trang 7 SGK Toán lớp 10  Tập 1: Cho mệnh đề Q: “Châu Á là châu lục có diện tích lớn nhất trên thế giới”. Phát biểu mệnh đề phủ định $\overline{Q}$ và xác định tính đúng sai của hai mệnh đề Q và $\overline{Q}$.

Phương pháp giải:

Bước 1: Phát biểu mệnh đề phủ định $\overline{Q}$ : thêm (hoặc bớt) từ không hoặc không phải vào trước vị ngữ của mệnh đề Q.

Bước 2: Xét tính đúng sai của mệnh đề Q.

Bước 3: Suy ra tính đúng sai của mệnh đề $\overline{Q}$. (Nếu Q đúng thì $\overline{Q}$  sai, còn nếu Q sai thì $\overline{Q}$  đúng.)

Lời giải:

Q: “Châu Á là châu lục có diện tích lớn nhất trên thế giới”.

Mệnh đề phủ định của Q là $\overline{Q}$: “Châu Á không phải là châu lục có diện tích lớn nhất trên thế giới”.

Vì Q là mệnh đề đúng nên $\overline{Q}$ là mệnh đề sai.

3. Mệnh đề kéo theo, mệnh đề đảo

Câu hỏi trang 8 Toán 10

HĐ3 trang 8 SGK Toán lớp 10 Tập 1: Cặp từ quan hệ nào sau đây phù hợp với vị trí bị che khuất trong câu ghép ở hình bên?

A. Nếu … thì …

B. Tuy … nhưng …

Lời giải:

Chọn A. Nếu … thì …

Nếu sử dụng rượu bia khi tham gia giao thông thì có thể bị xử phạt hành chính hoặc xử lí hình sự tùy theo mức độ vi phạm.

HĐ4 trang 8 SGK Toán lớp 10 Tập 1: Cho hai câu sau:

P: “Tam giác ABC là tam giác vuông tại A”;

Q: “Tam giác ABC có $A{B}^2+A{C}^2=B{C}^2$”.

Hãy phát biểu câu ghép có dạng “Nếu P thì Q”. 

Phương pháp giải:

Thay P, Q lần lượt bởi nội dung mệnh đề của nó.

Lời giải:

Phát biểu: “Nếu tam giác ABC là tam giác vuông tại A thì tam giác ABC có $A{B}^2+A{C}^2=B{C}^2$.”

HĐ5 trang 8 SGK Toán lớp 10 Tập 1: Xét hai câu sau:

P: “Phương trình bậc hai $a{x}^2+bx+c=0$ có hai nghiệm phân biệt”;

Q: “Phương trình bậc hai $a{x}^2+bx+c=0$ có biệt thức $\mathrm{\Delta }=b^2-4ac>0$”.

a) Hãy phát biểu mệnh đề $P\Rightarrow Q$.

b) Hãy phát biểu mệnh đề $Q\Rightarrow P$.

Phương pháp giải:

Mệnh đề $P\Rightarrow Q$ thường phát biểu ở dạng: “Nếu P thì Q”, “P suy ra Q”, “Vì P nên Q”.

Mệnh đề $Q\Rightarrow P$ thường phát biểu ở dạng: “Nếu Q thì P”, “Q suy ra P”, “Vì Q nên P”.

Thay P, Q lần lượt bởi nội dung mệnh đề vào câu ghép.

Lời giải:

Mệnh đề $P\Rightarrow Q$: “Nếu phương trình bậc hai $a{x}^2+bx+c=0$ có hai nghiệm phân biệt thì phương trình bậc hai $a{x}^2+bx+c=0$ có biệt thức $\mathrm{\Delta }=b^2-4ac>0$.”

Mệnh đề $Q\Rightarrow P$: “Nếu phương trình bậc hai $a{x}^2+bx+c=0$ có biệt thức $\mathrm{\Delta }=b^2-4ac>0$ thì phương trình bậc hai $a{x}^2+bx+c=0$ có hai nghiệm phân biệt.”

Câu hỏi trang 9 Toán 10

Luyện tập 3 trang 9 SGK Toán lớp 10 Tập 1: Cho các mệnh đề

P: “a và b chia hết cho c”;

Q: “a + b chia hết cho c”.

a) Hãy phát biểu định lí $P\Rightarrow Q$. Nêu giả thiết, kết luận của định lí và phát biểu định lí này dưới dạng điều kiện cần, điều kiện đủ.

b) Hãy phát biểu mệnh đề đảo của mệnh đề $P\Rightarrow Q$ rồi xác định tính đúng sai của mệnh đề đảo này.

Phương pháp giải:

Nếu một mệnh đề đúng có dạng $P\Rightarrow Q$ đúng, ta nói: P là giả thiết, Q là kết luận hoặc “P là điều kiện cần để có Q” hoặc “Q là điều kiện cần để có P”.

Mệnh đề đảo của mệnh đề $P\Rightarrow Q$ là mệnh đề $Q\Rightarrow P$.

Lời giải:

a) Mệnh đề $P\Rightarrow Q$, phát biểu là: “Nếu a và b chia hết cho c thì a + b chia hết cho c.”

Mệnh đề này đúng.

Giả thiết của định lí: a và b chia hết cho c

Kết luận của định lí: a + b chia hết cho c

Phát biểu định lí dưới dạng điều kiện cần là: “ a + b chia hết cho c là điều kiện cần để có a và b chia hết cho c”

Phát biểu định lí dưới dạng điều kiện đủ là: “ a và b chia hết cho c là điều kiện đủ để có a + b chia hết cho c”

b) Mệnh đề đảo của mệnh đề $P\Rightarrow Q$ là mệnh đề $Q\Rightarrow P$.

Mệnh đề $Q\Rightarrow P$: “Nếu a + b chia hết cho c thì a và b chia hết cho c”

Mệnh đề này sai.

Chẳng hạn a = 1 và b = 2, c =3. Ta có: $1+2=3⋮3$, nhưng 1 và 2 không chia hết cho 3.

4. Mệnh đề tương đương

HĐ6 trang 9 SGK Toán lớp 10 Tập 1: Hãy xác định tính đúng sai của mệnh đề sau:

 “Một số tự nhiên chia hết cho 5 nếu số đó có chữ số tận cùng bằng 0 hoặc 5 và ngược lại”.

Phương pháp giải:

+ Kiểm tra: $a⋮5\iff a$ tận cùng bằng 0 hoặc 5.

Lời giải:

Mệnh đề này đúng. (Dấu hiệu chia hết cho 5)

Luyện tập 4 trang 9 SGK Toán lớp 10 Tập 1: Phát biểu điều kiện cần và đủ để số tự nhiên n chia hết cho 2.

Phương pháp giải:

Ta nói: “P là điều kiện cần và đủ để có Q”  nếu $P\iff Q$ đúng

Lời giải:

Xét hai mệnh đề:

P: “Số tự nhiên n chia hết cho 2”

Q: “Số tự nhiên n có chữ số tận cùng là 0, 2, 4, 6, 8”

Ta có: mệnh đề $P\Rightarrow Q$ và mệnh đề $Q\Rightarrow P$ đều đúng. Vậy mệnh đề tương đương$P\iff Q$ đúng.

Phát biểu dưới dạng cần và đủ: “Số tự nhiên n có chữ số tận cùng là 0, 2, 4, 6, 8 là điều kiện cần và đủ để có số tự nhiên n chia hết cho 2”

Câu hỏi trang 10 Toán 10

Câu hỏi trang 10 SGK Toán lớp 10 Tập 1: Câu “Mọi số thực đều có bình phương không âm” là một mệnh đề. Có thể viết mệnh đề này như sau:

$P:"\mathrm{\forall }x\in ,x^2\ge 0"$

Câu “Có một số hữu tỉ mà bình phương của nó bằng 2” là một mệnh đề. Có thể viết mệnh đề này như sau: $Q:"\mathrm{\exists }x\in ,x^2=2"$

Em hãy xác định tính đúng sai của hai mệnh đề trên.

Lời giải:

Mệnh đề P đúng.

Mệnh đề Q sai.

5. Mệnh đề có chứa kí hiệu $\forall ,\exists$

Luyện tập 5 trang 10 SGK Toán lớp 10 Tập 1:  Phát biểu bằng lời mệnh đề sau và cho biết mệnh đề đó đúng hay sai.

"$\mathrm{\forall }x\in ,x^2+1\le 0.$"

Phương pháp giải:

Kí hiệu $\mathrm{\forall }$ phát biểu là “Với mọi”; “$x\in \mathbb{R}$” nghĩa là “x là số thực”.

Lời giải:

Phát biểu: “Với mọi số thực, tổng của bình phương của nó và 1 luôn nhỏ hơn 0”

Mệnh đề này sai.

Luyện tập 6 trang 10 SGK Toán lớp 10 tập 1: Trong tiết học môn Toán, Nam phát biểu: “Mọi số thực đều có bình phương khác 1”.

Mai phát biểu: “Có một số thực mà bình phương của nó bằng 1”

a) Hãycho biết bạn nào phát biểu đúng.

b) Dùng kí hiệu $\mathrm{\forall },\mathrm{\exists }$ để viết lại các phát biểu của Nam và Mai dưới dạng mệnh đề.

Phương pháp giải:

Kí hiệu $\mathrm{\forall }$ phát biểu là “Với mọi”; kí hiệu “$\mathrm{\exists }$” nghĩa là x “Tồn tại”/ “Có”/ “Có một”

Lời giải:

Trong tiết học môn Toán, Nam phát biểu: “Mọi số thực đều có bình phương khác 1”.

Mai phát biểu: “Có một số thực mà bình phương của nó bằng 1”

a) Phát biểu của Nam là sai. (chẳng hạn 1 và -1)

Phát biểu của Mai là đúng.

b) Phát biểu của Nam: "$\mathrm{\forall }x\in \mathbb{R},x^2\ne 1$".

Phát biểu của Mai: "$\mathrm{\exists }x\in \mathbb{Q},x^2=1$".

Bài tập

Câu hỏi trang 11 Toán 10

Bài 1.1 trang 11 SGK Toán lớp 10 tập 1: Trong các câu sau, câu nào là mệnh đề?

a) Trung Quốc là nước đông dân nhất thế giới;

b) bạn học trường nào?

c) Không được làm việc riêng trong giờ học;

d) Tôi sẽ sút bóng trúng xà ngang.

Lời giải:

Câu là mệnh đề là: a.

a) “Trung Quốc là nước đông dân nhất thế giới” là một mệnh đề.

b) “bạn học trường nào?” không là mệnh đề (do không xác định được tính đúng sai).

c) “Không được làm việc riêng trong giờ học” không là mệnh đề (do không xác định được tính đúng sai).

d) “Tôi sẽ sút bóng trúng xà ngang.” không là mệnh đề (do không xác định được tính đúng sai).

Bài 1.2 trang 11 SGK Toán lớp 10 Tập 1: Xác định tính đúng sai của mỗi mệnh đề sau:

a) $\pi <{\displaystyle \frac{10}{3}};$

b) Phương trình $3x+7=0$ có nghiệm;

c) Có ít nhất một số cộng với chính nó bằng 0;

d) 2022 là hợp số.

Lời giải:

a) Mệnh đề “$\pi <{\displaystyle \frac{10}{3}}$” đúng vì $\pi \approx 3,141592654<{\displaystyle \frac{10}{3}}=3,(3);$

b) Mệnh đề “Phương trình $3x+7=0$ có nghiệm” đúng vì $x={\displaystyle \frac{7}{3}}$ là nghiệm của phương trình.

c) Mệnh đề “Có ít nhất một số cộng với chính nó bằng 0” đúng vì 0 + 0 = 0

d) Mệnh đề “2022 là hợp số” đúng vì 2022 = 2.1011 = 3.673.

Bài 1.3 trang 11 SGK Toán lớp 10 Tập 1: Cho hai câu sau:

P: “Tam giác ABC là tam giác vuông”;

Q: “Tam giác ABC có một góc bằng tổng hai góc còn lại”

Hãy phát biểu mệnh đề tương đương $P\iff Q$ và xét tính đúng sai của mệnh đề này.

Lời giải:

Phát biểu: “Tam giác ABC là tam giác vuông khi và chỉ khi tam giác ABC có một góc bằng tổng hai góc còn lại”.

Mệnh đề này đúng.

Thật vậy, giả sử ba góc của tam giác ABC lần lượt là $x,y,z$ (đơn vị ${}^o$).

Ta có: tam giác ABC có một góc bằng tổng hai góc còn lại.

Không mất tính tổng quát, giả sử: $x=y+z$

$\iff 2x={180}^o$ (vì $x+y+x={180}^o$).

 $\iff x={90}^o$

Vậy tam giác ABC vuông.

Bài 1.4 trang 11 SGK Toán lớp 10 Tập 1: Phát biểu mệnh đề đảo của mỗi mệnh đề sau và xác định tính đúng sai của mệnh đề này.

P: “Nếu số tự nhiên n có chữ số tận cùng là 5 thì n chia hết cho 5”;

Q: “Nếu tứ giác ABCD là hình chữ nhật thì tứ giác ABCD có hai đường chéo bằng nhau”

Lời giải:

Mệnh đề đảo của mệnh đề P: “Nếu số tự nhiên n chia hết cho 5 thì n có chữ số tận cùng là 5”;

Mệnh đề này sai vì n còn có thể có chữ số tận cùng là 0. Chẳng hạn n = 10, chia hết cho 5 nhưng chữ số tận cùng bằng 0.

Mệnh đề đảo của mệnh đề Q: “Nếu tứ giác ABCD có hai đường chéo bằng nhau thì tứ giác ABCD là hình chữ nhật”

Mệnh đề này sai, chẳng hạn tứ giác ABCD (như hình dưới) - là hình thang cân – có hai đường chéo bằng nhau nhưng tứ giác ABCD không là hình chữ nhật

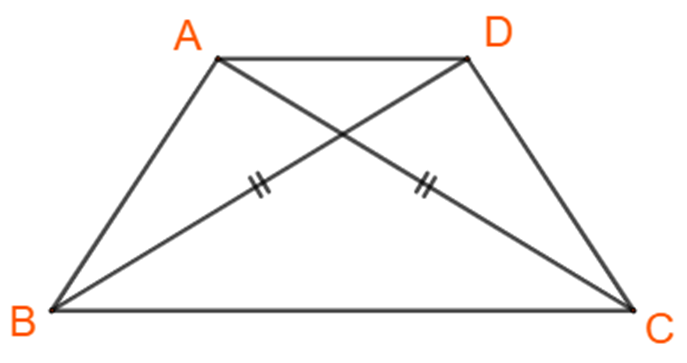
Bài 1.5 Trang 11 SGK Toán lớp 10 Tập 1: Với hai số thực a và b, xét mệnh đề P: “$a^2<b^2$” và Q: “$0<a<b$”

a) Hãy phát biểu mệnh đề $P\Rightarrow Q$;

b) Hãy phát biểu mệnh đề đảo của mệnh đề ở câu a.

c) Xác định tính đúng sai của mỗi mệnh đề ở câu a và câu b.

Phương pháp giải:

+) Mệnh đề kéo theo $P\Rightarrow Q$ được phát biểu là “Nếu P thì Q”

+) Mệnh đề đảo của mệnh đề $P\Rightarrow Q$ là mệnh đề $Q\Rightarrow P$

Lời giải:

a) Mệnh đề $P\Rightarrow Q$ là: “Nếu $a^2<b^2$ thì  $0<a<b$”

b) Mệnh đề $Q\Rightarrow P$ là: “Nếu $0<a<b$ thì $a^2<b^2$”

c) Mệnh đề $P\Rightarrow Q$ là: “Nếu $a^2<b^2$ thì  $0<a<b$” sai, chẳng hạn $a=-3;b=2$

 Mệnh đề $Q\Rightarrow P$ là: “Nếu $0<a<b$ thì $a^2<b^2$” đúng.

Bài 1.6 trang 11 SGK Toán lớp 10 Tập 1: Xác định tính đúng sai của mệnh đề sau và tìm mệnh đề phủ định của nó.

Q: “$\mathrm{\exists }n\in \mathbb{N},n$ chia hết cho $n+1$”

Phương pháp giải:

Phủ định của mệnh đề Q: “$\mathrm{\exists }n\in X,P(n)$” là mệnh đề $\overline{Q}$: “$\mathrm{\forall }n\in X,\overline{P(n)}$”) 

Lời giải:

Mệnh đề Q: “$\mathrm{\exists }n\in \mathbb{N},n$ chia hết cho $n+1$” đúng. Vì $\mathrm{\exists }0\in \mathbb{N},0⋮1$.

Mệnh đề phủ định của mệnh đề Q, kí hiệu $\overline{Q}$ là: “$\mathrm{\forall }n\in \mathbb{N},n$ không chia hết cho $n+1$”

Bài 1.7 trang 11 SGK Toán lớp 10 Tập 1: Dùng kí hiệu $\mathrm{\forall },\mathrm{\exists }$ đề viết các mệnh đề sau:

P: “Mọi số tự nhiên đều có bình phương lớn hơn hoặc bằng chính nó”

Q: “Có một số thực cộng với chính nó bằng 0”

Lời giải:

P: "$\mathrm{\forall }n\in ,n^2\ge n".$

Q: "$\mathrm{\exists }a\in ,a+a=0".$

Lý thuyết Bài 1: Mệnh đề

1. Mệnh đề là câu khẳng định có thể xác định được tính đúng hay sai của nó. Một mệnh đề không thể vừa đúng, vừa sai.

2. Mệnh đề chứa biến là câu khẳng định mà sự đúng hay sai của nó còn tùy thuộc vào một hay nhiều yếu tố biến đổi.

Ví dụ: Câu "Số nguyên $n$ chia hết cho $3$" không phải là mệnh đề, vì không thể xác định được nó đúng hay sai.

Nếu ta gán cho $n$ giá trị $n=4$ thì ta có thể có một mệnh đề sai.

Nếu gán cho $n$ giá trị $n=9$ thì ta có một mệnh đề đúng.

3. Phủ định của một mệnh đề $A$, là một mệnh đề, kí hiệu là $\overline{A}$. Hai mệnh đề $A$ và $\overline{A}$ là hai câu khẳng định trái ngược nhau.

Nếu $A$ đúng thì $\overline{A}$ sai.

Nếu $A$ sai thì $\overline{A}$ đúng.

Ví dụ: Cho mệnh đề A: "5 là số nguyên tố".

Đây là mệnh đề đúng.

Mệnh đề phủ định: "5 không là số nguyên tố"

Đây là mệnh đề sai.

4. Mệnh đề kéo theo

Mệnh đề kéo theo có dạng: "Nếu $A$ thì $B$", trong đó $A$ và $B$ là hai mệnh đề. Mệnh đề "Nếu $A$ thì $B$" kí hiệu là $A\Rightarrow B$. Tính đúng, sai của mệnh đề kéo theo như sau:

Mệnh đề $A\Rightarrow B$ chỉ sai khi $A$ đúng và $B$ sai.

Ví dụ: Cho hai mệnh đề $A$:"3 chia hết cho 2" và $B$:"4 là số chẵn"

Khi đó $A\Rightarrow B$ phát biểu là: "Nếu 3 chia hết cho 2 thì 4 là số chẵn"

Đây là mệnh đề đúng vì $A$ sai, $B$ đúng. (Mệnh đề $A$ sai nhưng không ảnh hướng đến tính đúng của mệnh đề $B$ nên mệnh đề kéo theo vẫn đúng).

5. Mệnh đề đảo

Mệnh đề "$B\Rightarrow A$" là mệnh đề đảo của mệnh đề $A\Rightarrow B$. Mệnh đề này chỉ sai khi $B$ đúng, $A$ sai.

Ví dụ: Trong ví dụ trên, mệnh đề $B\Rightarrow A$ phát biểu là: "Nếu 4 là số chẵn thì 3 chia hết cho 2"

Mệnh đề này sai vì $B$ đúng, $A$ sai.

6. Mệnh đề tương đương

Nếu $A\Rightarrow B$ là một mệnh đề đúng và mệnh đề $B\Rightarrow A$ cũng là một mệnh đề đúng thì ta nói $A$ tương đương với $B$, kí hiệu: $A\iff B$.

Khi $A\iff B$, ta cũng nói $A$ là điều kiện cần và đủ để có $B$ hoặc $A$ khi và chỉ khi $B$ hay $A$ nếu và chỉ nếu $B$.

Ví dụ: Cho hai mệnh đề $A$:"6 chia hết cho 2" và $B$:"4 là số chẵn"

Khi đó mệnh đề $A$ và $B$ đều đúng nên $A\iff B$ phát biểu là "6 chia hết cho 2 khi và chỉ khi 4 là số chẵn"

7. Kí hiệu $\forall$, kí hiệu $\exists$

Cho mệnh đề chứa biến: $P(x)$, trong đó $x$ là biến nhận giá trị từ tập hợp $X$.

- Câu khẳng định: Với mọi $x$ thuộc $X$ thì $P(x)$ là mệnh đề đúng và được kí hiệu là:  $\forall x\in X:P(x)$.

- Câu khẳng định: Có ít nhất một $x\in X$ (hay tồn tại $x\in X$) để $P(x)$ là mệnh đề đúng, kí hiệu là $\exists x\in X:P(x)$.

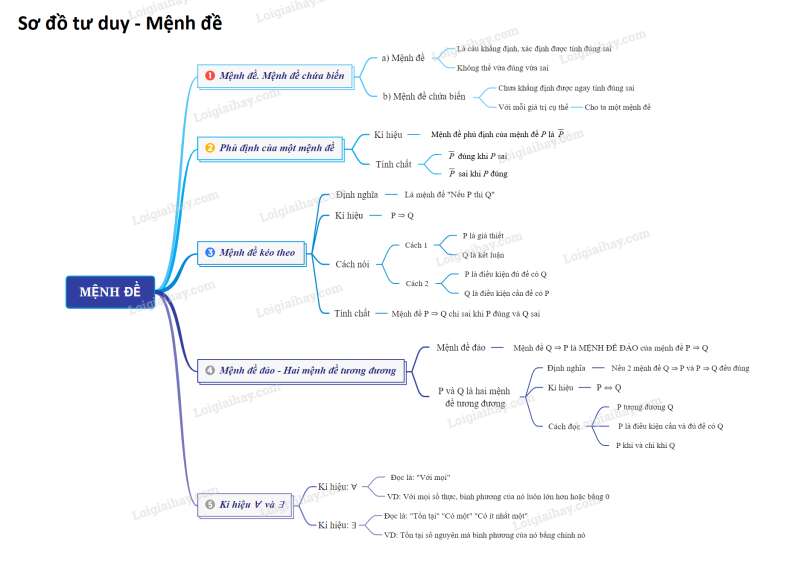
Sơ đồ tư duy - Mệnh đề