Toptailieu.vn giới thiệu Giải SGK Toán 10 Bài tập cuối chương 1 (Kết nối tri thức) giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 10 Tập 1. Mời các bạn đón xem:
Nội dung bài viết
Toán 10 Kết nối tri thức: Bài tập cuối chương 1
A. Trắc nghiệm
Bài 1.17 trang 20 SGK Toán lớp 10 Tập 1: Câu nào sau đây không là mệnh đề?
A. Tam giác đều là tam giác có ba cạnh bằng nhau.
B. 3<1
C. 4−5=1
D. Bạn học giỏi quá!
Phương pháp giải:
Mệnh đề là những câu, phát biểu đúng hoặc sai, không thể vừa đúng vừa sai.
Lời giải:
A. “Tam giác đều là tam giác có ba cạnh bằng nhau.” Là một mệnh đề.
B. “3<1” là một mệnh đề.
C. “4−5=1” là một mệnh đề.
D. “Bạn học giỏi quá!” không là một mệnh đề.
Chọn đáp án D.
A. Hai tam giác bằng nhau là điều kiện cần để diện tích của chúng bằng nhau.
B. Hai tam giác bằng nhau là điều kiện cần và đủ để diện tích của chúng bằng nhau
C. Hai tam giác có diện tích bằng nhau là điều kiện đủ để chúng bằng nhau
D. Hai tam giác bằng nhau là điều kiện đủ để diện tích của chúng bằng nhau
Phương pháp giải:
“P là điều kiện đủ để có Q” hoặc “Q là điều kiện cần để có P” nếu mệnh đề P⇒Q đúng.
“P là điều kiện cần và đủ để có Q” nếu mệnh đề P⇔Q đúng.
Lời giải:
Xét hai mệnh đề:
P: “Hai tam giác bằng nhau”
Q: “Hai tam giác có diện tích bằng nhau”
A. Hai tam giác bằng nhau là điều kiện cần để diện tích của chúng bằng nhau.
Mệnh đề “P là điều kiện cần để có Q”. Ta kiểm tra mệnh đề Q⇒P
Dễ thấy “Hai tam giác có diện tích bằng nhau” không suy ra “Hai tam giác bằng nhau”
Chẳng hạn: ΔABC và ΔDEFđều có diện tích (12cm2) nhưng chúng không bằng nhau.
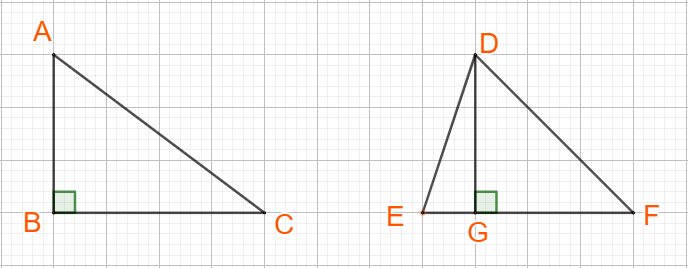
Vậy mệnh đề Q⇒P sai.
Đáp án A sai
B. Hai tam giác bằng nhau là điều kiện cần và đủ để diện tích của chúng bằng nhau
Mệnh đề “P là điều kiện cần và đủ để có Q”. Ta kiểm tra mệnh đề P⇔Q
Vì Q⧸⇒P nên P⧸⇔Q
Vậy mệnh đề P⇔Qsai
Đáp án B sai
C. Hai tam giác có diện tích bằng nhau là điều kiện đủ để chúng bằng nhau
Mệnh đề “Q là điều kiện đủ để có P”. Ta kiểm tra mệnh đề Q⇒P
Theo ý A, mệnh đề Q⇒P sai.
Vậy đáp án C sai
D. Hai tam giác bằng nhau là điều kiện đủ để diện tích của chúng bằng nhau
Mệnh đề “P là điều kiện đủ để có Q”. Ta kiểm tra mệnh đề P⇒Q
Dễ thấy “Hai tam giác bằng nhau” thì (hiển nhiên) suy ra“Hai tam giác có diện tích bằng nhau”
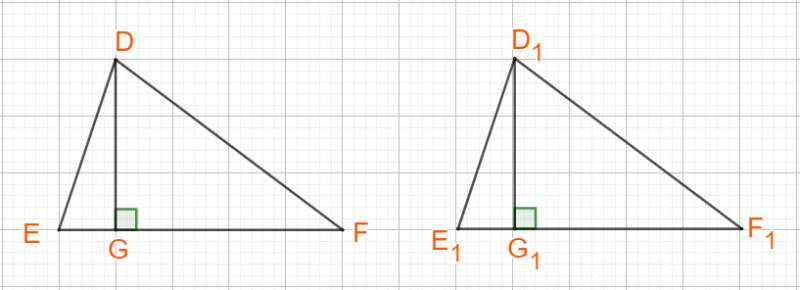
Vậy mệnh đề P⇒Q đúng.
Đáp án D đúng.
Chọn đáp án D.
Bài 1.19 trang 20 SGK Toán lớp 10 Tập 1: Mệnh đề nào sau đây là đúng?
A. ∀x∈R,x2>1⇒x>−1
B. ∀x∈R,x2>1⇒x>1
C. ∀x∈R,x>−1⇒x2>1
D. ∀x∈R,x>1⇒x2>1
Lời giải:
A. ∀x∈R,x2>1⇒x>−1
Sai, chẳng hạn với x=−2 thì x2=4>1 nhưng x=−2<−1.
B. ∀x∈R,x2>1⇒x>1
Sai, chẳng hạn với x=−2 thì x2=4>1 nhưng x=−2<1.
C. ∀x∈R,x>−1⇒x2>1
Sai, chẳng hạn với x=0>−1 nhưng x2=0<1
D. ∀x∈R,x>1⇒x2>1
Đúng.
Chọn đáp án D
Bài 1.20 trang 20 SGK Toán lớp 10 Tập 1: Cho tập hợp A = {a;b;c}. Tập A có bao nhiêu tập con?
A. 4
B. 6
C. 8
D. 10
Phương pháp giải:
Liệt kê các tập con (có 0,1,2,3 phần tử) của tập A.
Lời giải:
Tập A có các tập con là:
+) tập hợp rỗng.
+) tập con có 1 phần tử: {a}, {b}, {c}
+) tập con có 2 phần tử: {a;b}, {b;c}, {c;a}
+) tập con có 3 phần tử: {a;b;c} ( là tập A)
Vậy tập A có 8 tập hợp con.
Chọn đáp án C.
Chú ý khi giải
+ Khi tính số tập hợp con, mọi tập A luôn có 2 tập con là tập ∅ và chính nó.
+ Số tập hợp con của tập hợp A có n phần tử là: 2n
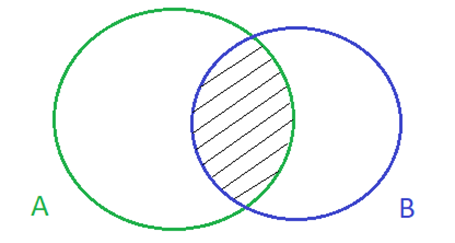
A. A∩B
B. A∖B
C. A∪B
D. B∖A
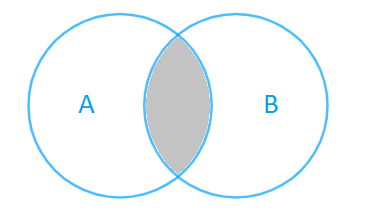
Phương pháp giải:
A∩B={x∈A|x∈B}
A∖B={x∈A|x∉B}
A∪B= {x∈A hoặc x∈B}
B∖A={x∈B|x∉A}
Lời giải:
Phần màu xám là phần giao nhau giữa tập hợp A và tập hợp B: vừa thuộc A, vừa thuộc B.
Do đó phần màu xám là A∩B
Chọn đáp án A
B. Tự luận
Bài 1.22 trang 20 SGK Toán lớp 10 Tập 1: Biểu diễn các tập hợp sau bằng biểu đồ Ven:
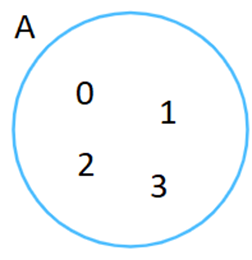
a) A={0;1;2;3}
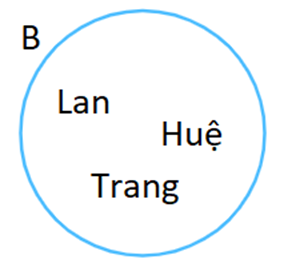
b) B = {Lan; Huệ; Trang}
Phương pháp giải:
Minh họa: Tập hợp P = {a; b; c}
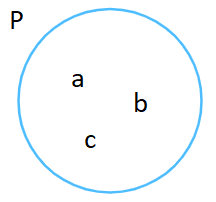
Lời giải:
a) A={0;1;2;3}. Biểu đồ Ven:
b) B = {Lan; Huệ; Trang}. Biểu đồ Ven:

Lời giải:
Ta có:
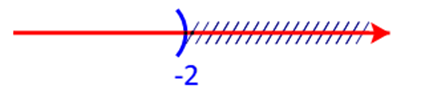
Biểu diễn khoảng (−∞;−2)
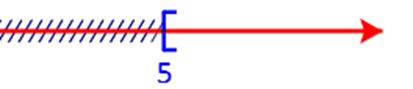
Biểu diễn nửa khoảng [5;+∞)
Vậy phần không bị gạch trên trục số là (−∞;−2)∪[5;+∞)
Cách 2:
Dễ thấy phần không gạch trên trục số là phần bù của [2;5)

Vậy phần không bị gạch trên trục số là R∖[2;5)=(−∞;−2)∪[5;+∞).
Bài 1.24 trang 20 SGK Toán lớp 10 Tập 1: Cho A={x∈Z|x<7}, B={1;2;3;6;7;8}. Xác định các tập hợp sau:
A∪B,A∩B,A∖B
Lời giải:
A={6;5;4;3;2;1;0;−1;−2;...}
B={1;2;3;6;7;8}
Vậy
A∩B={1;2;3;6}
A∪B={8;7;6;5;4;3;2;1;0;−1;−2;...}={x∈Z|x<9}
A∖B={5;4;0;−1;−2;−3;...}
Bài 1.25 trang 21 SGK Toán lớp 10 Tập 1: Cho A=[2;3],B=(1;+∞). Xác định các tập hợp sau:
A∪B,A∩B và CRB
Phương pháp giải:
Biểu diễn các tập hợp trên trục số
Lời giải:
Ta có:
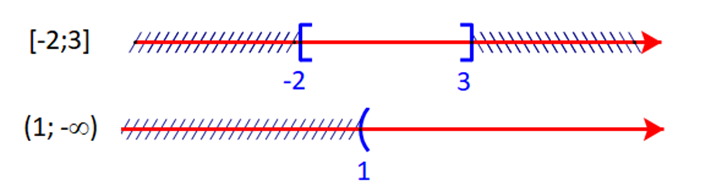
Giao của hai tập hợp là [−2;3]∩(1;+∞)=(1;3]
Hợp của hai tập hợp là [−2;3]∪(1;+∞)=[−2;+∞)
Phần bù của B trong R là: CRB=R∖(1;+∞)=(−∞;1]
Bài 1.26 trang 21 SGK Toán lớp 10 Tập 1: Xác định các tập hợp sau và biểu diễn chúng trên trục số.
a) (−∞;1)∩(0;+∞)
b) (4;7]∪(−1;5)
c) (4;7]∖(−3;5]
Phương pháp giải:
Biểu diễn các tập hợp trên trục số
Lời giải:
a) Ta có:
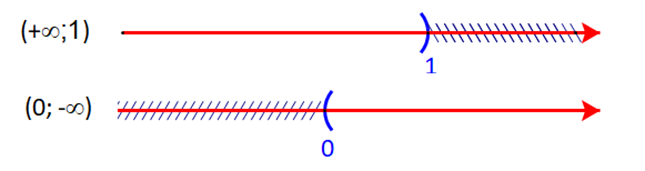

Giao của hai tập hợp là (−∞;1)∩(0;+∞)=(0;1)
b) Ta có:
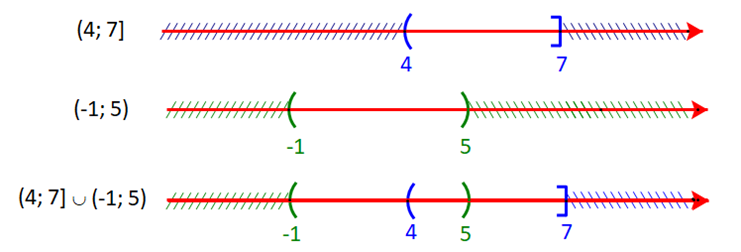
Hợp của hai tập hợp là (4;7]∪(−1;5)=(−1;7]
c) Ta có:
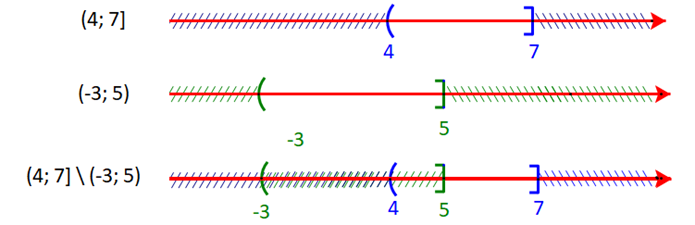
Hiệu của tập hợp (4;7] và tập hợp (−3;5] là (4;7]∖(−3;5]=(5;7]
Phương pháp giải:
Số khách du lịch đến cả hai địa điểm = Số khách đến động Thiên Cung + Số khách đến đảo Titop - Tổng số khách du lịch.
Lời giải:
Gọi A là tập hợp các khách du lịch đến thăm động Thiên Cung
B là tập hợp các khách du lịch đến đảo Titop.
⇒n(A)=789;n(B)=690;n(A∪B)=1410
Biểu đồ Ven
Tổng số khách du lịch = Số khách đến động Thiên Cung + Số khách đến đảo Titop - Số khách du lịch đến cả hai địa điểm.
Hay n(A∪B)=n(A)+n(B)−n(A∩B)
⇔1410=789+690−n(A∩B)⇔n(A∩B)=69
Vậy có 69 khách du lịch vừa đến thăm động Thiên cung vừa đến thăm đảo Titop ở vịnh Hạ Long.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.