Toptailieu.vn giới thiệu Giải bài tập Toán lớp 6 Bài tập cuối Chương 1 sách Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán lớp 6 Tập 1. Mời các bạn đón xem:
Nội dung bài viết
Toán 6 (Chân trời sáng tạo) Bài tập cuối Chương 1
Toán 6 trang 45-46 Câu hỏi trắc nghiệm
Câu 1
Gọi X là tập hợp các chữ cái trong từ " thanh”. Cách viết đúng là:
(A) X = {t; h; a; n; h}.
(B) X = {t; h; n};
(C) X= {t; h; a; n}.
(D) X = {t; h; a; n; m}.
Phương pháp giải:
Các phần tử của tập hợp được viết trong 2 dấu ngoặc nhọn{}, cách nhau bởi dấu chấm phảy. Mỗi phần tử được liệt kê 1 lần, thứ tự tùy ý
Lời giải
X = {t; h; a; n; h}.
Đáp án: A
Câu 2
Gọi X là tập hợp các số tự nhiên không lớn hơn 5. Cách viết sai là:
(A) X = {0; 1; 2; 3; 4; 5}.
(B) X = {0; 2; 4; 1; 3; 5}.
(C) X= {x ∈ N | x < 5}.
(D) X = {x ∈ N | x ≤ 5}.
Phương pháp giải:
Các phần tử của tập hợp được viết trong 2 dấu ngoặc nhọn{}, cách nhau bởi dấu chấm phảy. Mỗi phần tử được liệt kê 1 lần, thứ tự tùy ý
Lời giải
(C) sai vì thiếu phần tử 5
Đáp án: C
Câu 3
Cách viết nào sao đây là sai:
(A) a + b = b + a.
(B) ab = ba.
(C) ab + ac = a(b + c).
(D) ab - ac = a(c - b).
Phương pháp giải:
Tính chất của phép cộng và phép nhân số tự nhiên
Lời giải
(D) sai vì ab - ac=a(b-c)
Đáp án: D
Câu 4
Nhẩm xem kết quả phép tính nào dưới đây là đúng:
(A) 11 . 12 = 122.
(B) 13 . 99 = 1170.
(C) 14 . 99 = 1386.
(D) 45 . 9 = 415.
Phương pháp giải:
- Nhân 1 số có 2 chữ số với 11, ta giữ nguyên 2 chữ số của số đó và xen tổng của 2 chữ số đó vào giữa
- Nhân 1 số với 99, ta nhân số đó với 100 rồi trừ đi số đó
Lời giải
14 . 99 = 1386.
Đáp án: C
Câu 5
ƯCLN(18, 24) là:
(A) 24
(B) 18
(C) 12
(D) 6
Phương pháp giải:
Muốn tìm ƯCLN của hai hay nhiều số lớn hơn 1, ta thực hiện ba bước sau:
Bước 1: Phân tích mỗi số ra thừa số nguyên tố.
Bước 2: Chọn ra các thừa số nguyên tố chung.
Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất của nó.
Tích đó là ƯCLN phải tìm.
Lời giải
Ta có:
18 = 2 . 32
24 = 23 . 3
ƯCLN(18,24)=2.3=6
Đáp án:D
Câu 6
BCNN(3, 4, 6) là:
(A) 72
(B) 36
(C) 12
(D) 6
Phương pháp giải:
Muốn tìm BCNN của hai hay nhiều số lớn hơn 1, ta thực hiện ba bước sau:
Bước 1: Phân tích mỗi số ra thừa số nguyên tố.
Bước 2: Chọn ra các thừa số nguyên tố chung và riêng.
Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất của nó.
Tích đó là BCNN phải tìm.
Lời giải
3 = 3
4 =22
6 = 2.3
BCNN(3,4,6) = 22 . 3 = 12
Đáp án: C
Toán 6 trang 46 Bài 1: Tính giá trị của biểu thức (bằng cách hợp lí nếu có thể).
a) A = 37.173 + 62.173 +173;
b) B = 72.99 + 28.99 - 900;
c) C = 23.3 - (110+15):42;
d) D = 62:4.3 + 2.52 - 2010.
Phương pháp giải
- Áp dụng tính chất phân phối của phép nhân với phép cộng: a(b+c)=ab+ac
- Khi thực hiện các phép tính trong một biểu thức:
+ Đối với biểu thức không có dấu ngoặc:
theo thứ tự từ trái sang phải.
nâng lên luỹ thừa trước, rồi đến nhân và chia, cuối cùng đến cộng và trừ.
+ Đối với biểu thức có dấu ngoặc: Ta thực hiện phép tính trong ngoặc trước.
Lời giải
a) A = 37. 173 +62. 173 + 173
= 173. (37 +62 + 1)
= 173.100
= 17 300
b) B = 72.99 + 28.99 - 900
= 99. (72+28) - 900
= 99.100 - 900
= 9 900 - 900
= 9 000
c) C = 23.3-(110 + 15): 42
= 8.3 - (1 + 15): 42
= 8.3 - 16:42
= 8.3 - 1
= 23.
d) D = 62: 4.3 + 2.52 - 2100
= 36:4.3 + 2.25 - 1
= 27 + 50 - 1
= 76.
Toán 6 trang 46 bài 2: Tìm các chữ số x, y biết:
a) ¯12x02y¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯12x02y chia hết cho cả 2; 3 và 5.
b) ¯413x2y¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯413x2y chia hết cho 5 và 9 mà không chia hết cho 2.
Phương pháp giải
Các số có tận cùng là 0 hoặc 5 thì chia hết cho 5; các số có tận cùng là 0;2;4;6;8 thì chia hết cho 2 nên các số có tận cùng là 0 thì vừa chia hết cho 2, vừa chia hết cho 5; các số có tận cùng là 5 thì chia hết cho 5 nhưng không chia hết cho 2.
a) Các số có chữ số tận cùng là 0 và có tổng các chữ số chia hết cho 3 thì chia hết cho 2, 3 và 5.
b) Các số có tận cùng là 5 và có tổng các chữ số chia hết cho 9 thì chia hết cho 5 và 9 mà không chia hết cho 2.
Lời giải
a) ¯12x02y¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯12x02y chia hết cho 2 và 5 khi chữ số tận cùng của nó là 0.
=> y = 0
¯12x020¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯12x020 chia hết cho 3 khi tổng các chữ số của nó cũng chia hết cho 3.
Nên (1 + 2 + x + 0 + 2 + 0)⋮⋮3
=> (x + 5) ⋮⋮ 3 và 0≤x≤90≤x≤9
=> x∈∈ {1; 4; 7}
Vậy để ¯12x02y¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯12x02y chia hết cho 2, 3 và cả 5 thì y = 0 và x ∈∈{1; 4; 7}.
b) ¯413x2y¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯413x2y chia hết cho 5 mà không chia hết cho 2 khi chữ số tận cùng của nó là 5
=> y = 5
¯413x25¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯413x25chia hết cho 9 khi tổng các chữ số của nó cũng chia hết cho 9
Nên (4 + 1 + 3 + x + 2 + 5) ⋮⋮9
=> (x + 15) ⋮⋮9 và 0≤x≤90≤x≤9
=> x = 3.
Vậy ¯413x2y¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯413x2y chia hết cho 5 và 9 mà không chia hết cho 2 thì x = 3 và y = 5.
Toán 6 trang 46 Bài 3: Viết các tập hợp sau bằng cách liệt kê các phần tử:
a) A= {a ∈∈ N| 84 ⋮a; 180⋮ a và a > 6};
b) B = {b ∈N| b⋮12; b⋮15; b⋮18 và 0 < b < 300}.
Phương pháp giải
a) Tìm các ước chung của 84 và 180 mà lớn hơn 6
b) Tìm các bội chung của 12; 15 và 18 mà lớn hơn 0 nhỏ hơn 300
Lời giải
a) Theo đề bài: 84 chia hết cho a và 180 chia hết cho a nên a là ƯC(84, 180) và a > 6.
Ta có: 84 = 22.3.7
180 = 22. 32.5
ƯCLN(84, 180) = 22. 3 = 12
=> a ∈ ƯC(84, 180) = Ư(12) = {1; 2; 3; 4; 6; 12}
Mà a > 6.
=> a = 12.
Vậy tập hợp A = {12}
b) Vì b chia hết cho 12, b chia hết cho 15, b chia hết cho 18 nên b là BC(12, 15, 18) và 0 < b <300
Ta có: 12 = 22. 3; 15 = 3.5; 18 = 2.32
=> BCNN(12,15,18)=22.32.5=180
=> b∈ BC(12, 15, 18) = B(180) = {0; 180; 360;...}
Mà 0 < b < 300
=> b = 180
Vậy tập hợp B = {180}.
Trong thực tế các bạn đã bán được số lượng hàng như sau: trà sữa bán được 93 li, dừa bán được 64 quả. Hỏi lớp 6A đã thu được bao nhiêu tiền lãi? Lớp 6A có hoàn thành mục tiêu đã đề ra không?
Phương pháp giải
- Tìm số tiền lớp 6A bỏ ra để nhập hàng.
- Tìm số tiền lớp 6A bán được.
- Tìm số tiền lãi lớp 6A thu được
=> Kết luận
Lời giải

Số tiền lớp 6A bỏ ra để nhập hàng là:
100. 16 500 + 70 . 9 800 = 2 336 000 (đồng)
Số tiền lớp 6A bán được là:
93. 20 000 + 64 .15 000 = 2 820 000 (đồng)
Số tiền lãi lớp 6A thu được là:
2 820 000 - 2 336 000 = 484 000 (đồng) < 500 000 (đồng)
Vậy với mục tiêu số tiền lãi thu được là 500 000 đồng thì lớp 6A không hoàn thành mục tiêu đã đề ra.
Toán 6 trang 46 Bài 5: Thực vật được cấu tạo bởi các tế bào. Tế bào lớn lên đến một kích thước nhất định thì phân chia ra thành 2 tế bào con. Các tế bào con tiếp tục tăng kích thước và lại phân chia thành 4 tế bào, rồi thành 8 tế bào, ...
Hãy cho biết số tế bào con có được sau lần phân chia thứ tư, thứ năm, thứ sáu từ một tế bào ban đầu.
Phương pháp giải
Nhận xét số tế bào con sau các lần phân bào với lũy thừa cơ số 2.
Lời giải
Lần 1: Phân chia thành 2 tế bào con
Lần 2: Phân chia thành 4 tế bào con => 4 = 22
Lần 3: Phân chia thành 8 tế bào con => 8 = 23
=> Ta nhận thấy các tế bào phân chia theo lũy thừa của cơ số 2.
Vậy:
Số tế bào con có được sau lần phân chia thứ tư là 24 = 16 tế bào
Số tế bào con có được sau lần phân chia thứ năm là: 25 = 32 tế bào
Số tế bào con có được sau lần phân chia thứ sáu là: 26 = 64 tế bào.
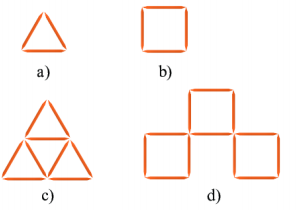
Phương pháp giải
Số hình xếp được = 36 : số que diêm ở mỗi hình
Lời giải
a) Huy xếp được: 36:3=12 hình
b) Huy xếp được: 36:4= 9 hình
c) Huy xếp được 36: 9 = 4 hình
d) Huy xếp được: 36:12=3 hình.
Toán 6 trang 46 Bài 7: a) Hoàn thiện bảng sau vào vở.
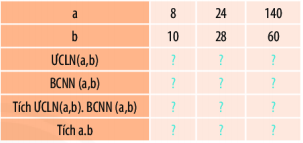
Phương pháp giải
- Muốn tìm ƯCLN của hai hay nhiều số lớn hơn 1, ta thực hiện ba bước sau:
Bước 1: Phân tích mỗi số ra thừa số nguyên tố.
Bước 2: Chọn ra các thừa số nguyên tố chung.
Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất của nó.
Tích đó là ƯCLN phải tìm.
- Muốn tìm BCNN của hai hay nhiều số lớn hơn 1, ta thực hiện ba bước sau:
Bước 1: Phân tích mỗi số ra thừa số nguyên tố.
Bước 2: Chọn ra các thừa số nguyên tố chung và riêng.
Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất của nó.
Tích đó là BCNN phải tìm.
Lời giải
|
a |
8 |
24 |
140 |
|
b |
10 |
28 |
60 |
|
ƯCLN(a, b) |
2 |
4 |
20 |
|
BCNN(a, b) |
40 |
168 |
420 |
|
ƯCLN(a, b) . BCNN(a, b) |
80 |
672 |
8400 |
|
a.b |
80 |
672 |
8400 |
b) Nhận xét: Nhìn vào bảng trên ta thấy tích ƯCLN(a, b) . BCNN(a, b) bằng với tích a . b.
Toán trang 47 Bài 8: Nhóm các bạn lớp 6B cần chia 48 quyển vở, 32 chiếc thước kẻ và 56 bút chì vào trong các túi quà để mang tặng các bạn trung tâm trẻ mồ côi sao cho số quyển vở, thước kẻ và bút chì ở mỗi túi đều như nhau. Tính số lượng túi quà nhiều nhất mà nhóm các bạn có thể chia được. Khi đó, số lượng vở, thước kẻ, bút chì trong mỗi túi là bao nhiêu?
Phương pháp giải
Số túi quà nhiều nhất có thể chia là ƯCLN của 48; 32 và 56
Lời giải
Gọi số túi quà nhiều nhất có thể chia được là x(túi, x∈N∗).
Theo đề bài ta có: 48⋮x;32⋮x;56⋮x
=> x∈ƯCLN(48; 32; 56)
Ta có: 48 = 24.3; 32 = 25; 56= 23.7
=> ƯCLN(48; 32; 56) =23 = 8.
=> x = 8
Vậy số túi quà nhiều nhất có thể chia được là 8 túi.
Toán 6 trang 47 Bài 9: Đố vui:
TOÁN VÀ THƠ
Trung thu gió mát trăng trong
Phố phường đông đúc, đèn lồng sao sa
Rủ nhau đi đếm đèn hoa
Quẩn quanh, quanh quẩn biết là ai hay
Kết năm, chẵn số đèn này
Bảy đèn kết lại còn hai ngọn thừa
Chín đèn thời bốn ngọn dư
Đèn hoa bao ngọn mà ngơ ngẩn lòng.
(Cho biết số đèn từ 600 đến 700 chiếc).
Phương pháp giải
- Dựa vào các câu thơ 5, 6, 7 ta suy ra số đèn chia hết cho 5, chia 7 dư 2, chia chín dư 4.
- Gợi ý cuối cùng ta có số đèn từ 600 đến 700 chiếc.
Lời giải
Gọi số đèn hoa là x(chiếc, x∈N∗)
Vì:
Kết năm, chẵn số đèn này
Bảy đèn kết lại còn hai ngọn thừa
Chín đèn thời bốn ngọn dư
Suy ra: số đèn chia hết cho 5, chia 7 dư 2, chia 9 dư 4.
=> x⋮5;(x−2)⋮7;(x−4)⋮9
Ta có: x⋮5; (x−2)⋮7;(x−4)⋮9
⇒ (x+5)⋮5; (x−2+7)⋮7;(x−4+9)⋮9
⇒(x+5)⋮5;(x+5)⋮7;(x+5)⋮9
⇒(x+5)∈BC(5,7,9)
Mà 5; 7 và 9 là các số đôi một nguyên tố cùng nhau nên BCNN(5, 7, 9) = 5.7.9 = 315.
⇒ BC(5, 7, 9) = B(315) = {0; 315; 630; 945;…}
⇒ (x + 5)∈ {0; 315; 630; 945;…}
⇒ x∈{310; 625; 940;…} (Do x∈N∗)
Mà 600 < x< 700 nên x = 625.
Vậy có 625 chiếc đèn hoa.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.