Toptailieu.vn giới thiệu Giải bài tập Toán lớp 10 Bài tập cuối chương I sách Cánh Diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 10 Tập 1. Mời các bạn đón xem:

Toán 10 Cánh diều: Bài tập cuối chương 1

Bài 1 trang 19 SGK Toán 10 tập 1 Phát biểu nào sau đây là một mệnh đề toán học?

a) Tích của ba số tự nhiên liên tiếp luôn chia hết cho 3.

b) Nếu $\widehat{AMB}={90}^o$ thì M nằm trên đường tròn đường kính AB.

c) Ngày 2 tháng 9 là ngày Quốc Khánh của nuốc Cộng hòa Xã hội chủ nghĩa Việt Nam

Lời giải:

a) Phát biểu “Tích của ba số tự nhiên liên tiếp luôn chia hết cho 3” là một mệnh đề toán học.

b) Phát biểu “Nếu $\widehat{AMB}={90}^o$ thì M nằm trên đường tròn đường kính AB” là một mệnh đề toán học.

c) Phát biểu “Ngày 2 tháng 9 là ngày Quốc Khánh của nuốc Cộng hòa Xã hội chủ nghĩa Việt Nam” không là một mệnh đề toán học (vì không liên quan đến sự kiện nào trong toán học).

Bài 2 trang 19 SGK Toán 10 tập 1 Lập mệnh đề phủ định của mỗi mệnh đề sau và nhận xét tính đúng sai của mệnh đề phủ định đó.

A: “Đồ thị hàm số y = x là một đường thẳng”

B: “Đồ thị hàm số $y=x^2$ đi qua điểm A (3; 6)”

Lời giải:

+) Mệnh đề phủ định của mệnh đề A là $\overline{A}$: “Đồ thị hàm số y = x không là một đường thẳng”

Mệnh đề $\overline{A}$ sai vì đồ thị hàm số y = x là một đường thẳng.

+) Mệnh đề phủ định của mệnh đề B là $\overline{B}$: “Đồ thị hàm số $y=x^2$ không đi qua điểm A (3; 6)”

Mệnh đề $\overline{B}$ đúng vì $6\ne 3^2$nên A (3;6) không thuộc đồ thị hàm số $y=x^2$.

Bài 3 trang 19 SGK Toán 10 tập 1 Cho tứ giác ABCD. Lập mệnh đề $P\Rightarrow Q$ và xét tính đúng sai của mệnh đề đó với:

a) P: “Tứ giác ABCD là hình chữ nhật”, Q: “Tứ giác ABCD là hình bình hành”

b) P: “Tứ giác ABCD là hình thoi”, Q: “Tứ giác ABCD là hình vuông”

Lời giải:

a) Mệnh đề $P\Rightarrow Q$ là: “Nếu tứ giác ABCD là hình chữ nhật thì tứ giác ABCD là hình bình hành”

Đúng vì mỗi hình chữ nhật đều là hình bình hành.

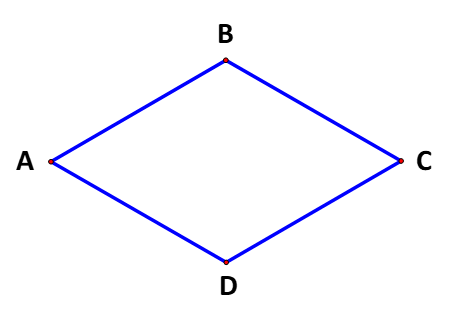
b) Mệnh đề $P\Rightarrow Q$ là: “Nếu tứ giác ABCD là hình thoi thì tứ giác ABCD là hình vuông”

Sai vì hầu hết các hình thoi không là hình vuông, chẳng hạn:

Bài 4 trang 19 SGK Toán 10 tập 1 Lập mệnh đề phủ định của mỗi mệnh đề sau:

A: “$\mathrm{\forall }x\in \mathbb{R},|x|\ge x$”

B: “$\mathrm{\forall }x\in \mathbb{R},x+\frac{1}{x}\ge 2$”

C: “$\mathrm{\exists }x\in \mathbb{Z},2x^2+3x-2=0$”

D: “$\mathrm{\exists }x\in \mathbb{Z},x^2<x$”

Lời giải:

Phủ định của mệnh đề A là mệnh đề “$\mathrm{\exists }x\in \mathbb{R},|x|\le x$”

Phủ định của mệnh đề B là mệnh đề “$\mathrm{\exists }x\in \mathbb{R},x+\frac{1}{x}\le 2$”

Phủ định của mệnh đề C là mệnh đề “$\mathrm{\forall }x\in \mathbb{Z},2x^2+3x-2\ne 0$”

Phủ định của mệnh đề D là mệnh đề “$\mathrm{\forall }x\in \mathbb{Z},x^2>x$”

Bài 5 trang 19 SGK Toán 10 tập 1 Dùng kí hiệu để viết mỗi tập hợp sau và biểu diễn mỗi tập hợp đó trên trục số:

a) $A=\{x\in \mathbb{R}|-2<x<-1\}$

b) $B=\{x\in \mathbb{R}|-3\le x\le 0\}$

c) $C=\{x\in \mathbb{R}|x\le 1\}$

d) $D=\{x\in \mathbb{R}|x>-2\}$

Lời giải:

a) Tập hợp A là khoảng (-2;1) và được biểu diễn là:

b) Tập hợp B là đoạn [-3; 0] và được biểu diễn là:

c) Tập hợp B là nửa khoảng $(-\mathrm{\infty };1]$ và được biểu diễn là:

d) Tập hợp B là nửa khoảng $(-\mathrm{\infty };1]$ và được biểu diễn là:

Bài 6 trang 19 SGK Toán 10 tập 1: Giải Bóng đá vô địch thế giới World Cup 2018 được tổ chức ở Liên bang Nga gồm 32 đội. Sau vòng thi đấu bảng, Ban tổ chức chọn ra 16 đội chia làm 8 cặp đấu loại trực tiếp. Sau vòng đấu loại trực tiếp đó, Ban tổ chức tiếp tục chọn ra 8 đội chia làm 4 cặp đấu loại trực tiếp ở vòng tứ kết. Gọi A là tập hợp 32 đội tham gia World Cup 2018, B là tập hợp 16 đội sau vòng thi đấu bảng, C là tập hợp 8 đội thi đấu vòng tứ kết.

a) Sắp xếp các tập hợp A, B, C theo quan hệ “$\subset$”.

b) So sánh hai tập hợp $A\cap C$ và $B\cap C$.

c) Tập hợp $A\mathrm{\setminus }B$ gồm những đội bóng bị loại sau vòng đấu nào?

Lời giải:

a) Ta có: A là tập hợp 32 đội tham gia World Cup 2018.

B là tập hợp 16 đội sau vòng thi đấu bảng (chọn từ 32 đội của tập hợp A sau thi thi đấu theo bảng)

Rõ ràng mỗi phần tử (mỗi đội) của tập hợp B cũng là một phần tử (một đội) của tập hợp A.

Do đó: $B\subset A$

Tương tự: Từ 16 đội của B, sau khi đấu loại trực tiếp, còn lại 8 đội vào tứ kết kí hiệu là tập hợp C

Do đó: $C\subset B$

Vậy $C\subset B\subset A$.

b) Tập hợp $A\cap C$ gồm các đội bóng vừa thuộc 32 đội tham gia World Cup 2018, vừa thuộc 8 đội thi đấu vòng tứ kết, chính là 8 đội của tập hợp C.

Tập hợp $B\cap C$ gồm các đội bóng vừa thuộc 16 đội sau vòng thi đấu bảng, vừa thuộc 8 đội thi đấu vòng tứ kết, chính là 8 đội của tập hợp C.

Vậy $A\cap C=B\cap C=C$

c) Tập hợp $A\mathrm{\setminus }B$ gồm các đội thuộc 32 đội tham gia World Cup 2018 nhưng không thuộc 16 đội sau vòng thi đấu bảng.

Vậy đó là 16 đội không vượt qua vòng thi đấu bảng.

Nói cách khác: Tập hợp $A\mathrm{\setminus }B$ gồm các đội bóng bị loại sau vòng đấu bảng.

Bài 7 trang 19 SGK Toán 10 tập 1 Cho hai tập hợp: $A=[0;3]$, $B=(2;+\mathrm{\infty })$. Xác định $A\cap B,A\cup B,$$A\mathrm{\setminus }B,B\mathrm{\setminus }A,\mathbb{R}\mathrm{\setminus }B.$

Lời giải:

+) $A\cap B=[0;3]\cap (2;+\mathrm{\infty })=(2;3]$

+) $A\cup B=[0;3]\cup (2;+\mathrm{\infty })=[0;+\mathrm{\infty })$

+) $A\mathrm{\setminus }B=[0;3]\mathrm{\setminus }(2;+\mathrm{\infty })=[0;2]$

+) $B\mathrm{\setminus }A=(2;+\mathrm{\infty })\mathrm{\setminus }[0;3]=(3;+\mathrm{\infty })$

+) $\mathbb{R}\mathrm{\setminus }B=\mathbb{R}\mathrm{\setminus }(2;+\mathrm{\infty })=(-\mathrm{\infty };2]$

Bài 8 trang 19 SGK Toán 10 tập 1 Gọi M là tập nghiệm của phương trình $x^2-2x-3=0$.

N là tập nghiệm của phương trình $(x+1)(2x-3)=0$

Tìm $P=M\cap N$.

Lời giải:

Ta có:

$x^2-2x-3=0\iff (x+1)(x-3)=0$

$\iff [\begin{array}{l}x=-1\\ x=3\end{array}\Rightarrow M=\{-1;3\}$

Lại có: $(x+1)(2x-3)=0\iff [\begin{array}{l}x=-1\\ x=\frac{3}{2}\end{array}$

$\Rightarrow N=\left\{-1;\frac{3}{2}\right\}$

$\Rightarrow P=M\cap N=\left\{-1\right\}$.