Với giải Câu hỏi trang  31 Toán 10 Tập 2 Kết nối tri thức chi tiết trong Bài 19: Phương trình đường thẳng giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem: 

SBT Toán 10 Kết nối tri thức trang 31 Bài 19: Phương trình đường thẳng

Bài 7.1 trang 31 SBT Toán 10 Tập 2: Trong mặt phẳng Oxy, cho điểm D(0; 2) và hai vectơ $\overrightarrow{n}=(1;-3),\overrightarrow{u}=(1;3)$.

a) Viết phương trình tổng quát của đường thẳng d đi qua D và nhận $\overrightarrow{n}$ là một vectơ pháp tuyến.

b) Viết phương trình tham số của đường thẳng Δ đi qua D và nhận $\overrightarrow{u}$ là một vectơ chỉ phương.

Lời giải:

a)

Phương trình tổng quát của đường thẳng d đi qua D và nhận là một vectơ pháp tuyến là:

1(x – 0) – 3(y – 2) = 0

⇔ x – 3y + 6 = 0

Vậy d: x – 3y + 6 = 0.

b)

Phương trình tham số của đường thẳng ∆ đi qua D và nhận là một vectơ chỉ phương là:

Bài 7.2 trang 31 SBT Toán 10 Tập 2: Trong mặt phẳng Oxy, cho ba điểm A(1; 2), B(0; –1) và C(–2; 3). Lập phương trình tổng quát của đường thẳng qua A và vuông góc với đường thẳng BC.

Lời giải:

Đường thẳng d qua A và vuông góc với đường thẳng BC nhận vectơ $\overrightarrow{BC}$ làm vectơ pháp tuyến.

$\overrightarrow{BC}$ = (–2 – 0; 3 + 1) = (–2; 4)

Phương trình của đường thẳng d là:

–2(x – 1) + 4(y – 2) = 0

⇔ –2x + 2 + 4y – 8 = 0

⇔ –2x + 4y – 6 = 0

⇔ x – 2y + 3 = 0

Vậy d: x – 2y + 3 = 0.

Bài 7.3 trang 31 SBT Toán 10 Tập 2: Trong mặt phẳng Oxy, cho hai điểm A(1; 2) và B(2; 3). Tìm một vectơ chỉ phương của đường thẳng AB và viết phương trình tham số của đường thẳng AB

Lời giải:

Một vectơ chỉ phương của đường thẳng AB chính là vectơ $\overrightarrow{AB}$.

Ta có: $\overrightarrow{AB}$ = (1; 1)

Đường thẳng AB đi qua điểm A(1; 2) có vectơ chỉ phương $\overrightarrow{AB}$ = (1; 1) có phương trình tham số là: 

Bài 7.4 trang 31 SBT Toán 10 Tập 2: Trong mặt phẳng Oxy, cho đường thẳng ∆: 2x – y + 5 = 0. Tìm tất cả các vectơ pháp tuyến có độ dài $2\sqrt{5}$ của đường thẳng ∆.

Lời giải:

Dựa vào phương trình tổng quát của đường thẳng ∆: 2x – y + 5 = 0. Đường thẳng ∆ có một vectơ pháp tuyến là $\overrightarrow{n}=(2;-1)$ nên các vectơ pháp tuyến của ∆ có dạng là $\overrightarrow{n\text{'}}=(2t;-t)$. Theo giả thiết ta có:

⇔ 4t² + t² = 20

⇔ 5t² = 20

⇔ t² = 4

⇔ t = ±2

Với t = 2, ta được vectơ pháp tuyến thỏa mãn yêu cầu đề bài là: $\overrightarrow{n_1\text{'}}$ = (4; –2)

Với t = – 2, ta được vectơ pháp tuyến thỏa mãn yêu cầu đề bài là: $\overrightarrow{n_2\text{'}}$ = (–4; 2).

Vậy có hai vectơ pháp tuyến thỏa mãn là $\overrightarrow{n_1\text{'}}$ = (4; –2) và $\overrightarrow{n_2\text{'}}$ = (–4; 2).

Bài 7.5 trang 31 SBT Toán 10 Tập 2: Trong mặt phẳng Oxy, cho đường thẳng d có phương trình y = –2x + 3. Viết phương trình tham số và phương trình tổng quát của đường thẳng d.

Lời giải:

Ta có: y = –2x + 3 ⇔ 2x + y – 3 = 0

Phương trình tổng quát của đường thẳng d là: 2x + y – 3 = 0.

Từ phương trình tổng quát ta thấy đường thẳng d: 2x + y – 3 = 0 có một vectơ pháp tuyến là: $\overrightarrow{n}$ = (2; 1), do đó, nó có một vectơ chỉ phương là $\overrightarrow{u}$ = (1; –2).

Thay x = 1 vào phương trình tổng quát ta có: y = 1.

Chọn điểm (1; 1) thuộc đường thẳng d: 2x + y – 3 = 0. Phương trình tham số của đường thẳng này là:

Bài 7.6 trang 31 SBT Toán 10 Tập 2: Trong mặt phẳng Oxy, cho điểm M(2; 1) và đường thẳng 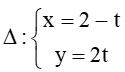. Tìm điểm N thuộc đường thẳng ∆ sao cho $MN=\sqrt{2}$

Lời giải:

Do N thuộc đường thẳng ∆ nên tọa độ của N có dạng: (2 – t; 2t).

Ta có: $\overrightarrow{MN}$ = (2 – t – 2; 2t – 1) = (–t; 2t – 1)

$MN=\sqrt{2}$

$\iff \sqrt{{(-t)}^2+{(2t-1)}^2}=\sqrt{2}$

⇔ (– t)² + (2t – 1)² = 2

⇔ t² + 4t² – 4t + 1 = 2

⇔ 5t² – 4t – 1 = 0

⇔ t = 1 hoặc t = $-\frac{1}{5}$

Với t = 1, ta có N(1; 2)

Với t = $-\frac{1}{5}$, ta có $N\left(\frac{11}{5};-\frac{2}{5}\right)$.

Vậy có hai điểm N thỏa mãn là N(1; 2) và $N\left(\frac{11}{5};-\frac{2}{5}\right)$.

Bài 7.7 trang 31 SBT Toán 10 Tập 2: Trong mặt phẳng Oxy, cho tam giác ABC có toạ độ ba đỉnh A(0; –1), B(2; 3) và C(–4; 1). Lập phương trình tham số của đường trung bình ứng với cạnh BC của tam giác ABC.

Lời giải:

Gọi d là đường trung bình ứng với cạnh BC của tam giác ABC nên d // BC và d đi qua trung điểm M của AB, do đó:

Đường thẳng d nhận vectơ $\overrightarrow{BC}$ = (–4 – 2; 1 – 3) = (–6; –2) là một vectơ chỉ phương.

Tọa độ trung điểm M là x_M = $\frac{0+2}{2}=1$; y_M = $\frac{(-1)+3}{2}=1$.

Suy ra M(1; 1) thuộc d.

Phương trình tham số của d là: