Với giải Câu hỏi trang 49 Toán 10 Tập 2 Kết nối tri thức chi tiết trong Bài tập cuối chương VII giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
SBT Toán 10 Kết nối tri thức trang 49: Bài tập cuối chương VII
Bài 7.49 trang 49 SBT Toán 10 Tập 2: Cho đường thẳng d: 4x + 3y – 2 = 0 và đường thẳng 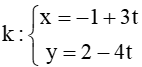 . Vị trí tương đối của hai đường thẳng d và k là
. Vị trí tương đối của hai đường thẳng d và k là
A. trùng nhau;
B. song song;
C. cắt nhau nhưng không vuông góc;
D. vuông góc.
Lời giải:
Đáp án đúng là: A
Đường thẳng d: 4x + 3y – 2 = 0 và đường thẳng 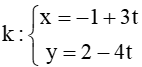 có vectơ pháp tuyến và vectơ chỉ phương lần lượt là: ,
có vectơ pháp tuyến và vectơ chỉ phương lần lượt là: ,
Do đó, đường thẳng k có vectơ pháp tuyến là: .
Do đó, nên d và k hoặc song song hoặc trùng nhau.
Xét điểm thuộc đường thẳng d.
Thay x = 1, y = vào phương trình tham số của đường thẳng k ta có:
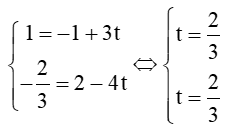
Do đó, cũng thuộc vào đường thẳng k
Vậy d và k trùng nhau.
Bài 7.50 trang 49 SBT Toán 10 Tập 2: Phương trình chính tắc của elip (E) đi qua điểm M(8; 0) và có tiêu cự bằng 6 là
A. ;
B. ;
C. ;
D. .
Lời giải:
Đáp án đúng là: D
Gọi phương trình chính tắc của elip (E) là: với a > b > 0
Elip (E) đi qua điểm M(8; 0) nên ta có:
⇔ a2 = 82 = 64
Mà tiêu cự là 2c = 6 ⇔ c = 3
Ta có:
Vậy phương trình chính tắc của elip (E) là: .
Bài 7.51 trang 49 SBT Toán 10 Tập 2: Cho điểm I(1; – 1) và đường thẳng d: x – y + 2 = 0. Phương trình đường tròn tâm I tiếp xúc với đường thẳng d là
A. (x – 1)2 + (y + 1)2 = 4;
B. (x + 1)2 + (y – 1)2 = 4;
C. (x – 1)2 + (y + 1)2 = 8;
D. (x + 1)2 + (y – 1)2 = 8.
Lời giải:
Đáp án đúng là: C
Đường tròn tâm I tiếp xúc với đường thẳng d nên ta có bán kính
R = d(I, d) = 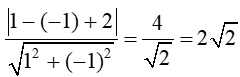
Phương trình đường tròn tâm I tiếp xúc với đường thẳng d là:
(x – 1)2 + (y + 1)2 = ()2
⇔ (x – 1)2 + (y + 1)2 = 8
Bài 7.52 trang 49 SBT Toán 10 Tập 2: Cho đường thẳng d: x – y + 3 = 0. Phương trình đường thẳng song song với d và cách d một khoảng là là
A. x + y + 1 = 0 và x + y + 3 = 0;
B. x – y – 1 = 0;
C. x – y + 3 = 0;
D. x – y + 3 = 0 và x – y – 1 = 0.
Lời giải:
Đáp án đúng là: (không có đáp án phù hợp)
Phương trình đường thẳng song song với d có dạng là: d’: x – y + c = 0 với c ≠ 3
Chọn điểm A(1; 4) thuộc đường thẳng d
Do d’ // d và d’ cách d một khoảng là nên ta có:
d(A, d’) =
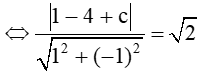
⇔ |c – 3| = 2 (*)
TH1: c – 3 ≥ 0 hay c ≥ 3
(*) ⇔ c – 3 = 2 ⇔ c = 5 (thỏa mãn)
TH2: c – 3 < 0 hay c < 3
(*) ⇔ –c + 3 = 2 ⇔ c = 1 (thỏa mãn)
Với c = 5 ta có, d’: x – y + 5 = 0.
Với c = 1 ta có, d’: x – y + 1 = 0.
Bài 7.53 trang 49 SBT Toán 10 Tập 2: Trong mặt phẳng Oxy, cho điểm M(–3; 2) và vectơ . Viết phương trình tham số của đường thẳng d đi qua M và nhận là một vectơ chỉ phương.
Lời giải:
Phương trình tham số của đường thẳng d đi qua M(–3; 2)và nhận là một vectơ chỉ phương là
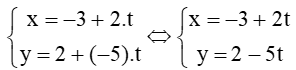
Bài 7.54 trang 49 SBT Toán 10 Tập 2: Trong mặt phẳng Oxy, cho điểm N(2; –1) và vectơ .Viết phương trình tổng quát của đường thẳng d đi qua N và nhận là một vectơ pháp tuyến.
Lời giải:
Phương trình tổng quát của đường thẳng d đi qua N và nhận là một vectơ pháp tuyến là:
3(x – 2) – 1(y + 1) = 0
⇔ 3x – y – 6 – 1 = 0
⇔ 3x – y – 7 = 0.
Bài 7.55 trang 49 SBT Toán 10 Tập 2: Cho tam giác ABC với A(1; –1), B(3; 5), C(–2; 4).
a) Viết phương trình tham số của đường thẳng AB.
b) Viết phương trình đường cao AH của tam giác ABC.
c) Tính khoảng cách từ điểm A đến đường thẳng BC.
d) Tính sin của góc giữa hai đường thẳng AB và AC.
Lời giải:
a)
Ta có là một vectơ chỉ phương của đường thẳng AB nên vectơ cũng là một vectơ chỉ phương của AB.
Đường thẳng AB đi qua điểm A(1; –1) và nhận là một vectơ chỉ phương có phương trình tham số là 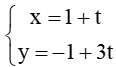
b)
Do AH vuông góc với BC nên là một vectơ pháp tuyến của đường cao AH.
Đường cao AH đi qua điểm A(1; –1) nhận là một vectơ pháp tuyến có phương trình tổng quát là:
5(x – 1) + 1(y + 1) = 0
⇔ 5x – 5 + y + 1 = 0
⇔ 5x + y – 4 = 0.
c)
Đường thẳng BC nhận vectơ là một vectơ chỉ phương nên BC nhận là một vectơ pháp tuyến.
Do đó phương trình đường thẳng BC là:
1(x – 3) – 5(y – 5) = 0
⇔ x – 3 – 5y + 25 = 0
⇔ x – 5y + 22 = 0.
Khoảng cách từ điểm A(1; –1) đến đường thẳng BC là
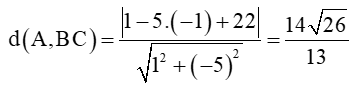
d)
Gọi α là góc giữa hai đường thẳng AB và AC có hai vectơ chỉ phương lần lượt là:
Khi đó
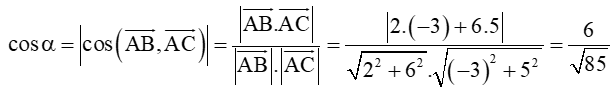
Do α là góc giữa hai đường thẳng nên sinα > 0.
Lại có sin2α + cos2α = 1.
Xem thêm các bài giải sách bài tập Toán lớp 10 Kết nối tri thức hay, chi tiết khác:
Bài 7.38 trang 47 SBT Toán 10 Tập 2: Trong các phương trình sau, phương trình nào là phương trình chính tắc của đường hypebol?...
Bài 7.39 trang 47 SBT Toán 10 Tập 2: Cho hai điểm A(–1; 0) và B(–2; 3). Phương trình đường thẳng đi qua B và vuông góc với AB là...
Bài 7.40 trang 47 SBT Toán 10 Tập 2: Cho điểm A(2; 3) và đường thẳng d: x + y + 3 = 0. Khoảng cách từ điểm A đến đường thẳng d là...
Bài 7.41 trang 47 SBT Toán 10 Tập 2: Cho hai đường thẳng d: x – 2y – 5 = 0 và k: x + 3y + 3 = 0. Góc giữa hai đường thẳng d và k là...
Bài 7.42 trang 48 SBT Toán 10 Tập 2: Cho đường tròn (C) có phương trình (x – 2)2 + (y + 3)2 = 9. Tâm I và bán kính R của đường tròn (C) là...
Bài 7.43 trang 48 SBT Toán 10 Tập 2: Cho elip (E) có phương trình . Điểm nào sau đây là một tiêu điểm của (E)?...
Bài 7.44 trang 48 SBT Toán 10 Tập 2: Đường thẳng qua A(1; –1) và B(–2; –4) có phương trình là...
Bài 7.45 trang 48 SBT Toán 10 Tập 2: Cho hypebol (H) có phương trình chính tắc .Tiêu cự của hypebol là...
Bài 7.46 trang 48 SBT Toán 10 Tập 2: Cho hai điểm A(0; – 2), B(2; 4). Phương trình đường tròn tâm A đi qua điểm B là...
Bài 7.47 trang 48 SBT Toán 10 Tập 2: Phương trình chính tắc của parabol (P) đi qua điểm E(2; 2) là...
Bài 7.48 trang 48 SBT Toán 10 Tập 2: Cho đường tròn (C) có phương trình (x + 1)2 + (y + 1)2 = 4 và điểm M(1; –1) thuộc đường tròn. Phương trình tiếp tuyến của đường tròn tại điểm M là...
Bài 7.49 trang 49 SBT Toán 10 Tập 2: Cho đường thẳng d: 4x + 3y – 2 = 0 và đường thẳng 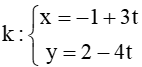 . Vị trí tương đối của hai đường thẳng d và k là...
. Vị trí tương đối của hai đường thẳng d và k là...
Bài 7.50 trang 49 SBT Toán 10 Tập 2: Phương trình chính tắc của elip (E) đi qua điểm M(8; 0) và có tiêu cự bằng 6 là...
Bài 7.51 trang 49 SBT Toán 10 Tập 2: Cho điểm I(1; – 1) và đường thẳng d: x – y + 2 = 0. Phương trình đường tròn tâm I tiếp xúc với đường thẳng d là...
Bài 7.52 trang 49 SBT Toán 10 Tập 2: Cho đường thẳng d: x – y + 3 = 0. Phương trình đường thẳng song song với d và cách d một khoảng là là...
Bài 7.53 trang 49 SBT Toán 10 Tập 2: Trong mặt phẳng Oxy, cho điểm M(–3; 2) và vectơ . Viết phương trình tham số của đường thẳng d đi qua M và nhận là một vectơ chỉ phương...
Bài 7.54 trang 49 SBT Toán 10 Tập 2: Trong mặt phẳng Oxy, cho điểm N(2; –1) và vectơ .Viết phương trình tổng quát của đường thẳng d đi qua N và nhận là một vectơ pháp tuyến...
Bài 7.55 trang 49 SBT Toán 10 Tập 2: Cho tam giác ABC với A(1; –1), B(3; 5), C(–2; 4)...
Bài 7.56 trang 50 SBT Toán 10 Tập 2: Trong mặt phẳng Oxy, cho hai điểm A(–1; 0) và B(3; 1)...
Bài 7.57 trang 50 SBT Toán 10 Tập 2: Cho đường tròn (C) có phương trình x2 + y2 – 4x + 6y – 12 = 0...
Bài 7.58 trang 50 SBT Toán 10 Tập 2: Các phương trình dưới đây là phương trình chính tắc của đường nào? Khi đó hãy tìm các tiêu điểm, tiêu cự, đường chuẩn (nếu là đường parabol)...
Bài 7.59 trang 50 SBT Toán 10 Tập 2: Cho elip (E) có phương trình là . Tìm toạ độ các điểm M thuộc (E), biết rằng M nhìn hai tiêu điểm của (E) dưới một góc vuông...
Bài 7.60 trang 50 SBT Toán 10 Tập 2: Lập phương trình chính tắc của parabol (P) biết rằng, (P) đi qua điểm A(2; 4). Khi đó hãy tìm điểm M thuộc (P) và cách tiêu điểm của (P) một khoảng bằng 5...
Bài 7.61 trang 50 SBT Toán 10 Tập 2: Hình vẽ bên minh hoạ một phòng thì thầm (whispering gallery) với mặt cắt ngang là một hình bán elip với chiều cao 24 feet và chiều rộng 80 feet...