Toán 10 Chân trời sáng tạo trang 46 Bài 2: Đường thẳng trong mặt phẳng toạ độ

Toán 10 Chân trời sáng tạo trang 46 Bài 2: Đường thẳng trong mặt phẳng toạ độ

Giang Ngày: 12-02-2023 Lớp 10

621

Với giải Câu hỏi trang 46 Toán 10 Tập 2 Chân trời sáng tạo trong Bài 2: Đường thẳng trong mặt phẳng toạ độ học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:

Toán 10 Chân trời sáng tạo trang 46 Bài 2: Đường thẳng trong mặt phẳng toạ độ

HĐ Khởi động trang 46 Toán 10 Tập 2: Tìm các giá trị của tham số a, b, c để phương trình ax+by+c = 0

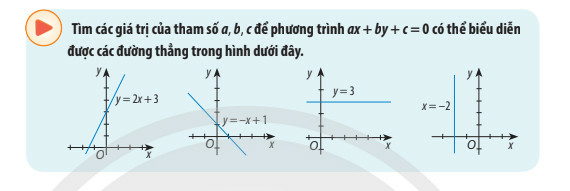
HĐ Khởi động trang 46 Toán 10 Tập 2 Chân trời sáng tạo (ảnh 1)

Lời giải

+) Hình 1: $y = 2 x + 3 \Rightarrow y - 2 x - 3 = 0$

Vậy $a = - 1, b = 1, c = - 3$

+) Hình 2: $y = - x + 1 \Rightarrow y + x - 1 = 0$

Vậy $a = 1, b = 1, c = - 1$

+) Hình 3: $y = 3 \Rightarrow y - 3 = 0$

Vậy $a = 0, b = 1, c = - 3$

+ Hình 4: $x = - 2 \Rightarrow x + 2 = 0$

Vậy $a = 1, b = 0, c = 2$

HĐ Khám phá 1 trang 46 Toán 10 Tập 2: Trong mặt phẳng Oxy, cho hai đường thẳng $Δ$ đi qua điểm $M_{0} (x_{0}; y_{0})$ và vectơ $\vec{n} = (a; b)$ và $\vec{u} = (b; - a)$ khác vectơ 0. Cho biết $\vec{u}$ có giá song song hoặc trùng với $Δ$ .

a) Tính tích vô hướng $\vec{n} \vec{. u}$ và nêu nhận xét về phương của hai vectơ $\vec{n}, \vec{u}$

b) Gọi $M (x; y)$ là điểm di động trên $Δ$ . Chứng tỏ rằng vectơ $\vec{M_{0} M}$ luôn cùng phương với vectơ $\vec{u}$ và luôn vuông góc với vectơ $\vec{n}$

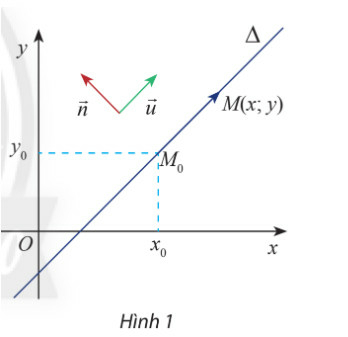
HĐ Khám phá 1 trang 46 Toán 10 Tập 2 Chân trời sáng tạo (ảnh 2)

Phương pháp giải:

a) +) Áp dụng ứng dụng biểu thức tọa độ của vectơ tính tích vô hướng

+) Dựa vào kết quả tích vô hướng các định phương (bằng 0 thì vuông góc)

b) +) Xác định tỉ lệ giũa các tọa độ của hai vectơ để so sánh về phương

+) Tính tích vô hướng để chứng minh vuông góc

Lời giải

a) Ta có $\vec{n} . \vec{u} = a . b + b . (- a) = 0$

Tích vô hướng bằng 0 nên hai vectơ $\vec{n}, \vec{u}$ có phương vuông góc với nhau

b) Vectơ $\vec{M_{0} M}$ có giá là đường thẳng $Δ$

=> luôn cùng phương với vectơ $\vec{u}$

=> vectơ $\vec{M_{0} M}$ có phương vuông góc với vectơ $\vec{n}$ .

Xem thêm các bài giải Toán 10 Chân trời sáng tạo hay, chi tiết khác:

HĐ Khởi động trang 46 Toán 10 Tập 2: Tìm các giá trị của tham số a, b, c để phương trình ax+by+c = 0...

HĐ Khám phá 1 trang 46 Toán 10 Tập 2: Trong mặt phẳng Oxy, cho hai đường thẳng $Δ$ đi qua điểm $M_{0} (x_{0}; y_{0})$ và vectơ $\vec{n} = (a; b)$ và $\vec{u} = (b; - a)$ khác vectơ 0. Cho biết $\vec{u}$ có giá song song hoặc trùng với $Δ$ ...

HĐ Khám phá 2 trang 47 Toán 10 Tập 2: Trong mặt phẳng Oxy, cho đường thẳng $Δ$ đi qua điểm $M_{0} (x_{0}; y_{0})$ và nhận $\vec{u} = (u_{1}; u_{2})$ là vectơ chỉ phương. Với mỗi điểm $M (x; y)$ thuộc $Δ$ , tìm tọa độ của điểm M theo tọa độ của $M_{0}$ và $\vec{u}$ ...

Thực hành 1 trang 47 Toán 10 Tập 2: a) Viết phương trình tham số của đường thẳng d đi qua điểm $B (- 9; 5)$ và nhận $\vec{v} = (8; - 4)$ là vectơ chỉ phương...

Vận dụng 1 trang 48 Toán 10 Tập 2: Một trò chơi đua xe ô tô vượt da mặt trên máy tính là xác định trước một hệ trục tọa độ Oxy. Cho biết một ô tô chuyển động thẳng đều từ điểm $M (1; 1)$ với Vectơ vận tốc $\vec{v} = (40; 30)$ ...

HĐ Khám phá 3 trang 48 Toán 10 Tập 2: Trong mặt phẳng Oxy, cho đường thẳng $Δ$ đi qua điểm $M_{0} (x_{0}; y_{0})$ và nhận $\vec{n} = (a; b)$ làm vectơ pháp tuyến. Với mỗi điểm $M (x; y)$ thuộc $Δ$ , chứng tỏ rằng điểm $M (x; y)$ có tọa độ thỏa mãn phương trình...

Thực hành 2 trang 49 Toán 10 Tập 2: Viết phương trình tham số và phương trình tổng quát của đường thẳng $Δ$ trong các trường hợp sau...

Vận dụng 2 trang 49 Toán 10 Tập 2: Một người đã lập trình một trò chơi trên máy tính. Trên màn hình máy tính đã xác định trước một hệ trục tọa độ Oxy. Người đó viết lệnh để một điểm $M (x; y)$ từ vị trí $A (1; 2)$ chuyển động thẳng đều với Vectơ vận tốc $\vec{v} = (3; - 4)$ ...

Thực hành 3 trang 51 Toán 10 Tập 2: Tìm các hàm số bậc nhất có đồ thị là các đường thẳng trong thực hành 2...

Vận dụng 3 trang 51 Toán 10 Tập 2: Một người bắt đầu mở một vòi nước. Nước từ vòi chảy với vận tốc là 2 $m^{3} / h$ vào một cái bể đã chứa sẵn 5 $m^{3}$ nước...

HĐ Khám phá 4 trang 51 Toán 10 Tập 2: Cho hai đường thẳng $Δ_{1}$ và $Δ_{2}$ một vectơ pháp tuyến lần lượt là $\vec{n_{1}}$ và $\vec{n_{2}}$ ...

Thực hành 4 trang 53 Toán 10 Tập 2: Xét vị trí tương đối của các cặp đường thẳng $d_{1}$ và $d_{2}$ trong các trường hợp sau...

Vận dụng 4 trang 53 Toán 10 Tập 2: Viết phương trình đường thẳng $d_{1}$ ...

HĐ Khám phá 5 trang 54 Toán 10 Tập 2: Cho hai đường thẳng xy và zt cắt nhau tại O và cho biết $\hat{x O z} = 38^{\circ}$ (hình 6)...

HĐ Khám phá 6 trang 54 Toán 10 Tập 2: Cho hai đường thẳng...

Thực hành 5 trang 56 Toán 10 Tập 2: Tìm số đo của góc giữa hai đường thẳng $Δ_{1}$ và $Δ_{2}$ trong các trường hợp sau...

Vận dụng 5 trang 56 Toán 10 Tập 2: Tìm số đo của góc giữa hai đường thẳng là đồ thị của hai hàm số $y = x$ và $y = 2 x + 1$ ...

HĐ Khám phá 7 trang 56 Toán 10 Tập 2: Trong mặt phẳng Oxy. Cho đường thẳng $Δ : a x + b y + c = 0 (a^{2} + b^{2} > 0)$ có vectơ pháp tuyến $\vec{n}$ và cho điểm $M_{0} (x_{0}; y_{0})$ có hình chiếu vuông góc $H (x_{H}; y_{H})$ trên $Δ$ (hình 9)...

Thực hành 6 trang 57 Toán 10 Tập 2: Trong mặt phẳng Oxy, cho tam giác ABC có tọa độ các đỉnh là $A (1; 1), B (5; 2), C (4; 4)$ . Tính độ dài các đường cao của tam giác ABC...

Vận dụng 6 trang 57 Toán 10 Tập 2: Tính khoảng cách giữa hai đường thẳng $d_{1} : 4 x - 3 y + 2 = 0$ và $d_{2} : 4 x - 3 y + 12 = 0$ ...

Bài 1 trang 57 Toán 10 Tập 2: Lập phương trình tham số và phương trình tổng quát của đường thẳng d trong mỗi trường hợp sau...

Bài 2 trang 57 Toán 10 Tập 2: Cho tam giác ABC biết $A (2; 5), B (1; 2)$ và $C (5; 4)$ ...

Bài 3 trang 57 Toán 10 Tập 2: Lập phương trình tham số và phương trình tổng quát của đường thẳng $Δ$ trong mỗi trường hợp sau...

Bài 4 trang 57 Toán 10 Tập 2: Xét vị trí tương đối của cặp đường thẳng $d_{1}$ và $d_{2}$ sau đây...

Bài 5 trang 58 Toán 10 Tập 2: Cho đường thẳng d có phương trình tham số ${\begin{cases} x = 2 - t \\ y = 5 + 3 t \end{cases}$ ...

Bài 6 trang 58 Toán 10 Tập 2: Tìm số đo của góc giữa hai đường thẳng $d_{1}$ và $d_{2}$ trong các trường hợp sau...

Bài 7 trang 58 Toán 10 Tập 2: Tính khoảng cách từ điểm M đến đường thẳng $Δ$ trong các trường hợp sau...

Bài 8 trang 58 Toán 10 Tập 2: Tính khoảng cách giữa hai đường thẳng $Δ : 3 x + 4 y - 10 = 0$ và $Δ^{'} : 6 x + 8 y - 1 = 0$ ...

Bài 9 trang 58 Toán 10 Tập 2: Trong mặt phẳng Oxy cho điểm $S (x; y)$ di động trên đường thẳng $d : 12 x - 5 y + 16 = 0$ . Tính khoảng cách ngắn nhất từ điểm $M (5; 10)$ đến điểm S...

Bài 10 trang 58 Toán 10 Tập 2: Một người đang viết chương trình cho trò chơi đá bóng robot. Gọi $A (- 1; 1), B (9; 6), C (5; - 3)$ là 3 vị trí trên màn hình...

Từ khóa :

Giải bài tập Toán 10

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

298

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

319

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

347

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

295

Tìm kiếm

Bài Viết Xem Nhiều

Bài Viết Cùng Lớp

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

2021 © All Rights Reserved.