Toán 10 Chân trời sáng tạo trang 67 Bài 4: Ba đường Conic trong mặt phẳng toạ độ

Toán 10 Chân trời sáng tạo trang 67 Bài 4: Ba đường Conic trong mặt phẳng toạ độ

Giang Ngày: 12-02-2023 Lớp 10

427

Với giải Câu hỏi trang 67 Toán 10 Tập 2 Chân trời sáng tạo trong Bài 4: Ba đường Conic trong mặt phẳng toạ độ học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:

Toán 10 Chân trời sáng tạo trang 67 Bài 4: Ba đường Conic trong mặt phẳng toạ độ

Thực hành 2 trang 67 Toán 10 Tập 2: Viết phương trình chính tắc của hypebol có tiêu cự bằng 10 và độ dài trục nhỏ bằng 6.

Phương pháp giải:

Phương trình chính tắc của hypebol có dạng $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ với $M (x; y) \in (H); b = \sqrt{c^{2} - a^{2}}$

Lời giải

Ta có: $2 c = 10 \Rightarrow c = 5, 2 b = 6 \Rightarrow b = 3$

Suy ra $a = \sqrt{c^{2} - b^{2}} = \sqrt{5^{2} - 3^{2}} = 4$

Vậy phương trình chính tắc của hypebol có dạng $\frac{x^{2}}{16} - \frac{y^{2}}{9} = 1$

Vận dụng 2 trang 67 Toán 10 Tập 2: Một tháp làm nguội của một nhà cát có mặt cắt là một hypebol có phương trình $\frac{x^{2}}{27^{2}} - \frac{y^{2}}{40^{2}} = 1$ (hình 9). Cho biết chiều cao của tháp là 120 m và khoảng cách từ nóc tháp đến tâm đối xứng của hypebol bằng một nửa khoảng cách từ tâm đối xứng đến đáy. Tìm bán kính đường tròn nóc và bán kính đường tròn đáy của tháp.

Vận dụng 2 trang 67 Toán 10 Tập 2 Chân trời sáng tạo (ảnh 1)

Phương pháp giải:

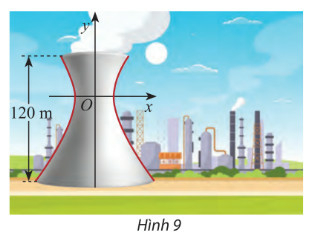
Bước 1: Xác định khoảng cách từ tâm đến đỉnh tháp và đáy tháp

Bước 2: Từ kết quả vừa tìm thay vào phương trình hypebol y bằng kết quả đó tìm x (Chỉ lấy kết quả dương)

Lời giải

Gọi khoảng cách từ tâm đối xứng đến đỉnh tháp là z

Suy ra khoảng cách từ tâm đối xứng đến đáy tháp là 2z

Ta có $z + 2 z = 120 \Rightarrow z = 40$

Thay $y = 40$ vào phương trình $\frac{x^{2}}{27^{2}} - \frac{y^{2}}{40^{2}} = 1$ ta tìm được $x = 27 \sqrt{2}$

Thay $y = 80$ vào phương trình $\frac{x^{2}}{27^{2}} - \frac{y^{2}}{40^{2}} = 1$ ta tìm được $x = 27 \sqrt{5}$

Vậy bán kính đường tròn nóc và bán kính đường tròn đáy của tháp lần lượt là $27 \sqrt{2}$ và $27 \sqrt{5}$

Xem thêm các bài giải Toán 10 Chân trời sáng tạo hay, chi tiết khác:

HĐ Khởi động trang 63 Toán 10 Tập 2: Nếu cắt mặt nón tròn xoay bởi mặt phẳng vuông góc với trục và không đi...

HĐ Khám phá 1 trang 64 Toán 10 Tập 2: Lấy một tấm bìa, ghim hai cái đinh lên đó tại hai điểm $F_{1}$ và $F_{2}$ . Lấy một vòng dây kín không đàn hồi có độ dài lớn hơn hai lần đoạn $F_{1} F_{2}$ ...

HĐ Khám phá 2 trang 64 Toán 10 Tập 2: Cho elip (E) có các tiêu điểm $F_{1}$ và $F_{2}$ và đặt $F_{1} F_{2} = 2 c$ . Chọn hệ trục tọa độ Oxy sao cho $F_{1} (- c; 0)$ và $F_{2} (c; 0)$ ...

Thực hành 1 trang 65 Toán 10 Tập 2: Viết phương trình chính tắc của elip trong hình 4...

Vận dụng 1 trang 65 Toán 10 Tập 2: Một đường hầm có mặt các hình nửa Elip cao 4 m, rộng 10 m (hình 5). Viết phương trình chính tắc của elip đó...

HĐ Khám phá 3 trang 65 Toán 10 Tập 2: Lấy một tấm bìa, trên đó đánh dấu hai điểm $F_{1}$ và $F_{2}$ . Lấy một cây thước thẳng với mép thước AB có chiều dài d và một đoạn dây không đàn hồi có chiều dài l sao cho $d - l = 2 a$ nhỏ hơn khoảng cách $F_{1} F_{2}$ (hình 6a)...

HĐ Khám phá 4 trang 66 Toán 10 Tập 2: Cho hyperbol (H) có các tiêu điểm $F_{1}$ và $F_{2}$ và đặt điểm $F_{1} F_{2} = 2 c$ . Chọn hệ trục tọa độ Oxy sao cho $F_{1} (- c; 0)$ và $F_{2} (c; 0)$ ...

Thực hành 2 trang 67 Toán 10 Tập 2: Viết phương trình chính tắc của hypebol có tiêu cự bằng 10 và độ dài trục nhỏ bằng 6...

Vận dụng 2 trang 67 Toán 10 Tập 2: Một tháp làm nguội của một nhà cát có mặt cắt là một hypebol có phương trình $\frac{x^{2}}{27^{2}} - \frac{y^{2}}{40^{2}} = 1$ (hình 9). Cho biết chiều cao của tháp là 120 m và khoảng cách từ nóc tháp đến tâm đối xứng của hypebol bằng một nửa khoảng cách từ tâm đối xứng đến đáy. Tìm bán kính đường tròn nóc và bán kính đường tròn đáy của tháp...

HĐ Khám phá 5 trang 68 Toán 10 Tập 2: Trong mặt phẳng Oxy, cho điểm $F (0; \frac{1}{2})$ , đường thẳng $Δ : y + \frac{1}{2} = 0$ và điểm $M (x; y)$ . Để tìm hệ thức giữa x và y sao cho $M$ cách đều F và $Δ$ , một học sinh đã làm như sau...

HĐ Khám phá 6 trang 68 Toán 10 Tập 2: Cho parabol (P) có tiêu điểm F và đường chuẩn $Δ$ . Gọi khoảng cách từ tiêu điểm đến đường chuẩn là p, hiển nhiên $p > 0$ ...

Thực hành 3 trang 70 Toán 10 Tập 2: Viết phương trình chính tắc của parabol (P) có đường chuẩn $Δ : x + 1 = 0$ ...

Vận dụng 3 trang 70 Toán 10 Tập 2: Một cổng chào có hình parabol cao 10 m và bề rộng của cổng tại chân cổng là 5 m. Tính bề rộng của cổng tại chỗ cách đỉnh 2 m...

Bài 1 trang 70 Toán 10 Tập 2: Viết phương trình chính tắc của...

Bài 2 trang 70 Toán 10 Tập 2: Viết phương trình chính tắc của các đường conic dưới đây. Gọi tên và tìm tọa độ của các tiêu điểm của chúng...

Bài 3 trang 70 Toán 10 Tập 2: Để cắt một bảng hiệu quảng cáo hình Elip có trục lớn là 80 cm và trục nhỏ là 40 cm từ một tấm ván ép hình chữ nhật có kích thước là 80 cm x 40 cm, người ta vẽ hình elip đó trên tấm ván ép như hướng dẫn sau...

Bài 4 trang 71 Toán 10 Tập 2: Một nhà vòm chứa máy bay có mặt cắt hình nửa elip cao 8 m, rộng 20 m (hình 16)...

Bài 5 trang 71 Toán 10 Tập 2: Một tháp làm nguội của một nhà máy có mặt cắt là hình hyperbol có phương trình $\frac{x^{2}}{28^{2}} - \frac{y^{2}}{42^{2}} = 1$ (hình 17). Biết chiều cao của tháp là 150 m và khoảng cách từ nóc tháp đến tâm đối xứng của hypebol là $\frac{2}{3}$ khoảng cách từ tâm đối xứng đến đáy. Tính bán kính nóc và bán kính đáy của tháp...

Bài 6 trang 71 Toán 10 Tập 2: Một cái cầu có dây cáp treo như hình vẽ parabol, cầu dài 100 m và được nâng đỡ bởi những thanh thẳng đứng treo từ cáp xuống, thanh dài nhất là 30m, thanh ngắn nhất là 6m (hình 18). Tính chiều dài của thanh cách điểm giữa cầu 18m...

Thử thách trang 73 Toán 10 Tập 2: Áp dụng tính chất quang học của parabol để giải quyết vẫn đề sau đây...

Từ khóa :

Giải bài tập Toán 10

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

298

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

319

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

347

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

295

Tìm kiếm

Bài Viết Xem Nhiều

Bài Viết Cùng Lớp

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

2021 © All Rights Reserved.